兩層單入單出的神經網路能做什麼

阿新 • • 發佈：2019-02-17

定義神經網路結構

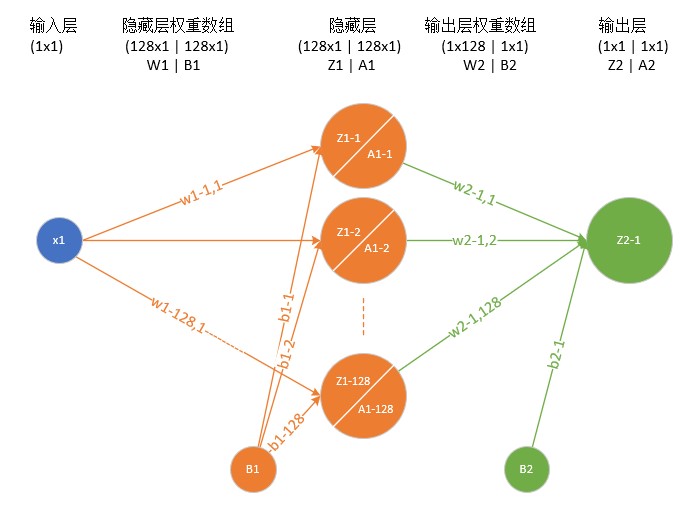
我們定義一個兩層的神經網路，輸入層不算，一個隱藏層，含128個神經元，一個輸出層。

數學理論證明：具有足夠數量神經元的兩層神經網路能夠擬合任意精度的連續函式。所以，今天咱們就用實際資料來驗證一下這個理論。我們假設一個連續函式的形式為：

\[y=0.4x^2 + 0.3xsin(15x) + 0.01cos(50x)-0.3\]

輸入層

輸入層就是一個標量X值。

權重矩陣W1/B1

它是連線兩層之間的紐帶，有的人理解它應該屬於輸入層，有的人理解應該屬於隱藏層，各有各的道理，我個人傾向於把它歸到隱藏層，理由是\(Z1=W1*X+B1\)，在X固定的前提下，W1決定了Z1的值。另外一個理由是B1的存在位置，在本例中B1是一個128x1的矩陣，它是隱藏層128個神經元的偏移，所以它應該屬於隱藏層。

其實這裡的B1所在的圓圈裡應該是個常數1，而B1連線到Z1-1...Z1-128的權重線B1-1...B1-128應該是個浮點數。我們為了說明問題方便，就寫了個B1，而實際的B1是指B1-1...B1-128的矩陣/向量。

W1的尺寸是128x1，B1的尺寸是128x1。

隱藏層

我們用一個128個神經元的網路來模擬函式，這個大家可以自己試驗一下，把程式碼中的神經元數量修改一下，然後在保持迭代次數和其它（超）引數不變的情況，看看最終的精確度有何區別，訓練時間的差異，以及記憶體佔用有何差異。

每個神經元的輸入\(Z1 = W1 * X + B1\)，我們在這裡使用雙曲sigmoid正切函式，所以輸出是\(A1 = sigmoid(Z1)\)

。當然也可以使用其它啟用函式如果tanh, Relu等等。

權重矩陣W2/B2

與W1/B1類似，我個人認為它屬於輸出層。W2的尺寸是1x128，B2的尺寸是1x1。

輸出層

由於我們只想完成一個擬合任務，所以輸出層只有一個神經元。它們的左側是\(Z2=W2*A1+B2\)，右側是\(A2=Z2\)。

為什麼在最後一步沒有用啟用函式，而是直接令A2=Z2呢？我們後面再說。

創造訓練資料

讓我們先自力更生創造一些模擬資料：

import numpy as np
import matplotlib.pyplot as plt
from pathlib import Path

def TargetFunction(x):
    p1 = 0.4 * (x**2)
    p2 = 0.3 * x * np.sin(15 * x)
    p3 = 0.01 * np.cos(50 * x)
    y = p1 + p2 + p3 - 0.3
    return y

def CreateSampleDataXY(m):
    S = np.random.random((m,2))
    S[:,1] = TargetFunction(S[:,0])
    return S

def CreateTestData(n):
    TX = np.linspace(0,1,100)
    TY = TargetFunction(TX)
    TZ = np.zeros(n)
    return TX, TY, TZ

其函式影象在[0,1]之間的樣子是：

生成的資料格式如下：

\[ \begin{pmatrix} x_1, y_1\\ x_2, y_2\\ \dots\\ x_m, y_m\\ \end{pmatrix} \]

其中，x就是上圖中藍色點的橫座標值，y是縱座標值。在[0,1]之外的函式曲線沒這麼複雜，似乎擬合起來沒什麼難度，所以我們特點選擇了[0,1]之間這一段來做試驗。

定義前向計算過程

至此，我們得到了以下一串公式：

\[Z1=W1*X+B1\]
\[A1=sigmoid(Z1)\]
\[Z2=W2*A1+B2\]
\[A2=Z2 \tag{這一步可以省略}\]

def ForwardCalculation(x, dictWeights):
    W1 = dictWeights["W1"]
    B1 = dictWeights["B1"]
    W2 = dictWeights["W2"]
    B2 = dictWeights["B2"]

    Z1 = np.dot(W1,x) + B1
    A1 = sigmoid(Z1)
    Z2 = np.dot(W2,A1) + B2
    A2 = Z2  # 這一步可以省略

    dictCache ={"A1": A1, "A2": A2}
    return A2, dictCache

由於引數較多，所以我們用一個dictionary(dictWeights)來儲存W,B這些引數，如果是更多層的神經網路，就會有更多的引數，我們這裡使用的還是一些最基本的引數。

定義代價函式

我們用傳統的均方差函式: \(loss = \frac{1}{2}(Z-Y)^2\)，其中，Z是每一次迭代的預測輸出，Y是樣本標籤資料。我們使用所有樣本參與訓練，因此損失函式實際為：

\[Loss = \frac{1}{2}(Z - Y) ^ 2\]

其中的分母中有個2，實際上是想在求導數時把這個2約掉，沒有什麼原則上的區別。

定義針對w和b的梯度函式

看一下計算圖，然後用鏈式求導法則反推：

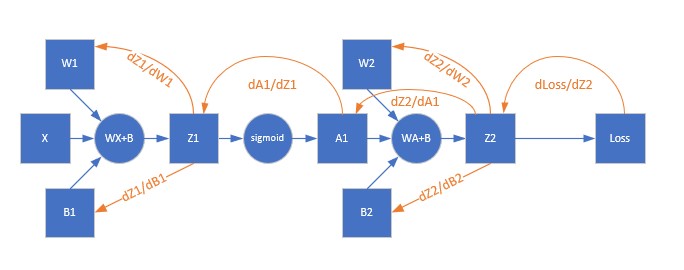
求W1的梯度

因為：

\[Z2 = W2*A1+B2\]

\[Loss = \frac{1}{2}(Z2-Y2)^2\]

所以我們用Loss的值作為基準，去求w對它的影響，也就是loss對w的偏導數：

\[ \frac{\partial{Loss}}{\partial{W2}} = \frac{\partial{Loss}}{\partial{Z2}}*\frac{\partial{Z2}}{\partial{W2}} \]

其中：

\[ \frac{\partial{Loss}}{\partial{Z2}} = \frac{\partial{}}{\partial{Z2}}[\frac{(Z2-Y)^2}{2}] = Z2-Y \]

而：

\[ \frac{\partial{Z2}}{\partial{W2}} = \frac{\partial{}}{\partial{W2}}(W2*A1+B2) = A1^T \]

所以：

\[ \frac{\partial{Loss}}{\partial{W2}} = \frac{\partial{Loss}}{\partial{Z2}}*\frac{\partial{Z}}{\partial{W2}} = (Z2-Y)*A1^T \]

矩陣求導的理論部分較為複雜，請大家參考我們的《基本數學導數公式》章節。

求B2的梯度

\[ \frac{\partial{Loss}}{\partial{B2}} = \frac{\partial{Loss}}{\partial{Z2}}*\frac{\partial{Z2}}{\partial{B2}} \]

其中第一項前面算w的時候已經有了，而：

\[ \frac{\partial{Z2}}{\partial{B2}} = \frac{\partial{(W2*A1+B2)}}{\partial{B2}} = 1 \]

所以：

\[ \frac{\partial{Loss}}{\partial{B2}} = \frac{\partial{Loss}}{\partial{Z2}}*\frac{\partial{Z2}}{\partial{B2}} = Z2-Y \]

求W1的梯度

因為：

\[A1 = sigmoid(Z1)\]

\[Z1 = W1*X+B1\]

對Z1求導：

\[ \frac{\partial{Loss}}{\partial{Z1}} = \frac{\partial{Loss}}{\partial{Z2}}*\frac{\partial{Z2}}{\partial{A1}}*\frac{\partial{A1}}{\partial{Z1}} \]

其中前面推導過：

\[ \frac{\partial{Loss}}{\partial{Z2}} = Z2-Y = dZ2 \]

而：

\[ \frac{\partial{Z2}}{\partial{A1}} = \frac{\partial{}}{\partial{A1}}(W2*A1+B2) = W2^T \]

\[ \frac{\partial{A1}}{\partial{Z1}} = \frac{\partial{}}{\partial{Z1}}(sigmoid(Z1)) = A1*(1-A1) \]

所以：

\[ \frac{\partial{Loss}}{\partial{Z1}} = W2^T * dZ2 * A1 * (1-A1) = dZ1 \]
而W1,B1的求導結果和W2,B2類似：

\[ \frac{\partial{Loss}}{\partial{W1}} = \frac{\partial{Loss}}{\partial{Z1}}*\frac{\partial{Z1}}{\partial{W1}}=dZ1*\frac{\partial{(W1*X+B1)}}{\partial{W1}}=dZ1*X^T \]

\[ \frac{\partial{Loss}}{\partial{B1}} = \frac{\partial{Loss}}{\partial{Z1}}*\frac{\partial{Z1}}{\partial{B1}}=dZ1*\frac{\partial{(W1*X+B1)}}{\partial{B1}}=dZ1 \]

變成程式碼：

def BackPropagation(x, y, dictCache, dictWeights):
    A1 = dictCache["A1"]
    A2 = dictCache["A2"]
    W2 = dictWeights["W2"]

    dLoss_Z2 = A2 - y
    dZ2 = dLoss_Z2
    dW2 = dZ2 * A1.T
    dB2 = dZ2

    dZ2_A1 = W2.T * dZ2
    dA1_Z1 = A1 * (1 - A1)
    # dZ1 is dLoss_Z1
    dZ1 = dZ2_A1 * dA1_Z1
    dW1 = dZ1 * x
    dB1 = dZ1

    dictGrads = {"dW1":dW1, "dB1":dB1, "dW2":dW2, "dB2":dB2}
    return dictGrads

每次迭代後更新w,b的值

def UpdateWeights(dictWeights, dictGrads, learningRate):
    W1 = dictWeights["W1"]
    B1 = dictWeights["B1"]
    W2 = dictWeights["W2"]
    B2 = dictWeights["B2"]

    dW1 = dictGrads["dW1"]
    dB1 = dictGrads["dB1"]
    dW2 = dictGrads["dW2"]
    dB2 = dictGrads["dB2"]

    W1 = W1 - learningRate * dW1
    W2 = W2 - learningRate * dW2
    B1 = B1 - learningRate * dB1
    B2 = B2 - learningRate * dB2

    dictWeights = {"W1": W1,"B1": B1,"W2": W2,"B2": B2}

    return dictWeights

幫助函式

第一個show_result函式用於最後輸出結果。第二個print_progress函式用於訓練過程中的輸出。

def sigmoid(x):
    s=1/(1+np.exp(-x))
    return s

def initialize_with_zeros(n_x,n_h,n_y):
    np.random.seed(2)
    # W1=np.random.randn(n_h,n_x)*0.00000001    # W1=np.random.randn(n_h,n_x)
    W1=np.random.uniform(-np.sqrt(6)/np.sqrt(n_x+n_h),np.sqrt(6)/np.sqrt(n_h+n_x),size=(n_h,n_x))
    # W1=np.reshape(32,784)
    B1=np.zeros((n_h,1))
    # W2=np.random.randn(n_y,n_h)*0.00000001  # W2=np.random.randn(n_y,n_h)
    W2=np.random.uniform(-np.sqrt(6)/np.sqrt(n_y+n_h),np.sqrt(6)/np.sqrt(n_y+n_h),size=(n_y,n_h))
    B2=np.zeros((n_y,1))

    assert (W1.shape == (n_h, n_x))
    assert (B1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (B2.shape == (n_y, 1))

    dictWeights = {"W1": W1,"B1": B1,"W2": W2,"B2": B2}

    return dictWeights

主程式初始化

m = 1000
S = CreateSampleDataXY(m)
#plt.scatter(S[:,0], S[:,1], 1)
#plt.show()
n_input, n_hidden, n_output = 1, 128, 1
learning_rate = 0.1
eps = 1e-10
dictWeights = initialize_with_zeros(n_input, n_hidden, n_output)
max_iteration = 1000
loss, prev_loss, diff_loss = 0, 0, 0

程式主迴圈

for iteration in range(max_iteration):
    for i in range(m):
        x = S[i,0]
        y = S[i,1]
        A2, dictCache = ForwardCalculation(x, dictWeights)
        dictGrads = BackPropagation(x,y,dictCache,dictWeights)
        dictWeights = UpdateWeights(dictWeights, dictGrads, learning_rate)
    print("iteration", iteration)

測試並輸出擬合結果

tm = 100
TX, TY, TZ = CreateTestData(tm)
correctCount = 0
for i in range(tm):
    x = TX[i]
    y = TY[i]
    a2, dict = ForwardCalculation(x, dictWeights)
    TZ[i] = a2

plt.scatter(TX, TY)
plt.plot(TX, TZ, 'r')
str = str.format("cell:{0} sample:{1} iteration:{2} rate:{3}", n_hidden, m, max_iteration, learning_rate)
plt.title(str)
plt.show()

上面的TX是[0,1]之間的連續數，共100個，間隔相同。TY是更加被模擬的函式計算出來的精確值。TZ是我們訓練的模型的預測值。我們的目的就是要比較TY和TZ之間的差距。
下圖就是擬合結果，還比較令人滿意。

引數調整

經常聽人說起“調參”，這次咱們親身經歷一下調參的痛（快）苦（樂）！我們下面一切的比較都是以下面這組引數為基準：

神經元數=128
輸入訓練資料量=1000
迭代次數=1000
權重調整步進值=0.1

以上這些標準值如何得到呢？試了很多組合後得到的，這就是所謂“試錯”的過程了。

神經元數量的變化（標準值128）

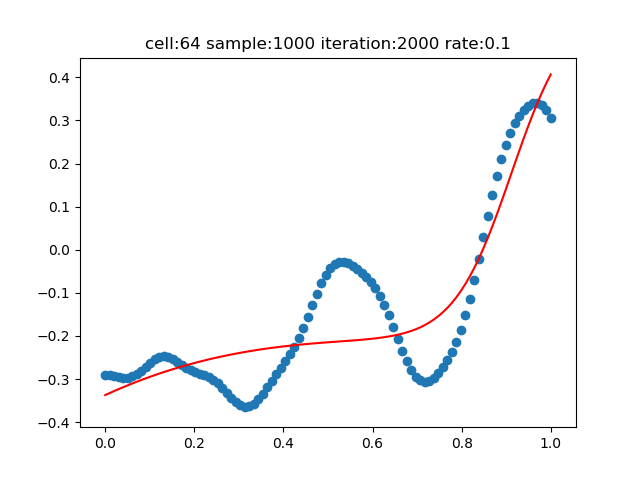
神經元數量=64

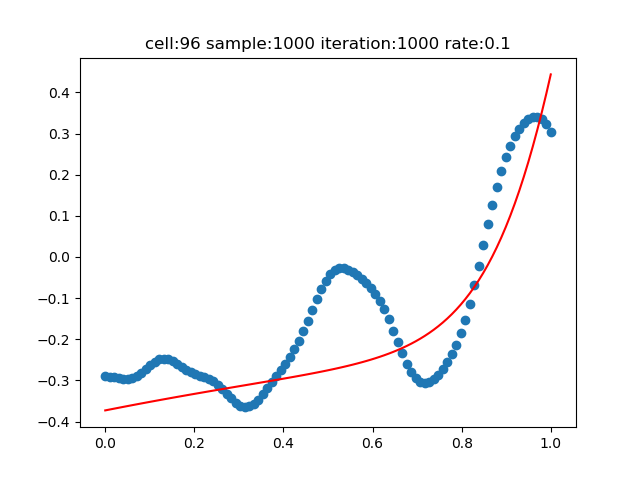
神經元數量=96

神經元數量=256，迭代次數=500

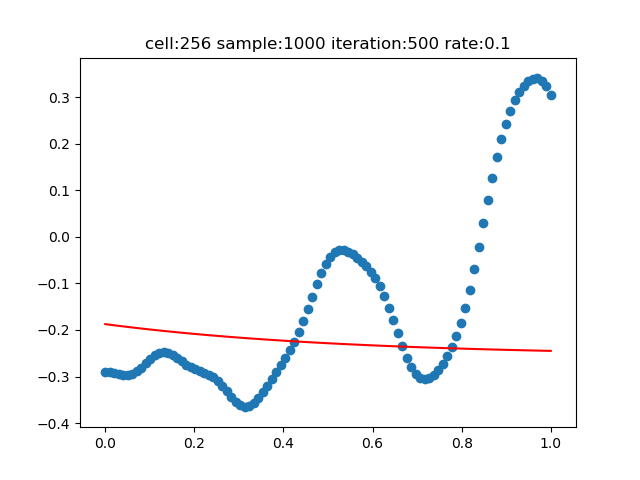
基準神經元數為128，在96時，擬合效果很差，在64時，儘管我們增加了迭代次數為2000，仍然很差。
第三張圖，儘管神經元數量翻了一倍，成為256個，但是迭代次數為500，少了一倍，也會造成奇怪的結果。

樣本量的變化（標準值1000）

輸入資料量=500

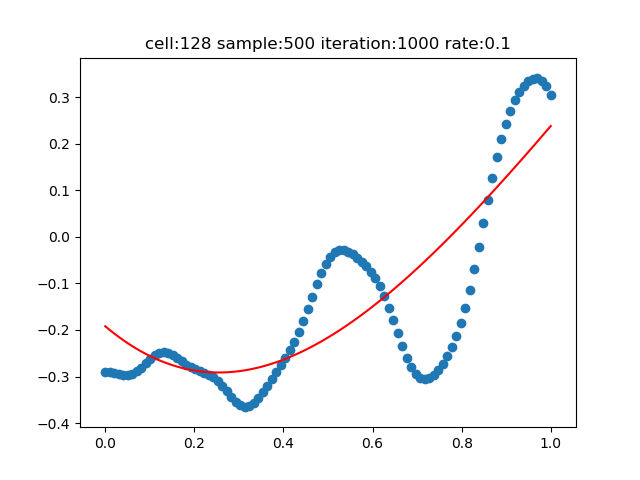
輸入資料量=1500

樣本資料量不夠時，擬合效果不好。但是當樣本資料量超過一定值後，就沒多大作用了。

迭代次數的變化（標準值1000）

迭代次數=500

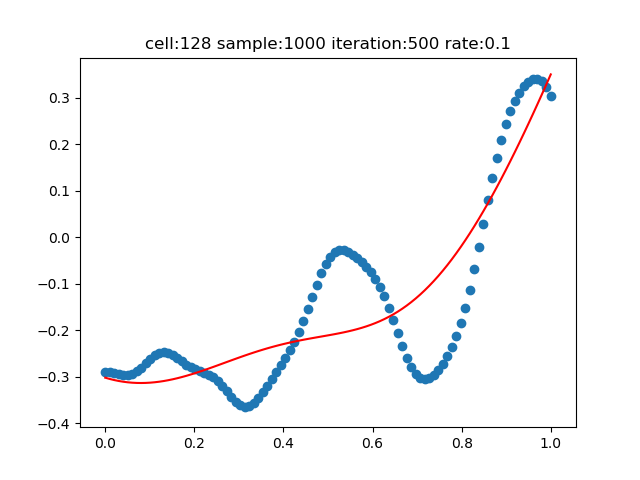
輸入資料量=1500

迭代次數少，擬合效果不好。迭代次數超過一定值後，容易造成過擬合，效果不大。

步長值的變化（標準值0.1）

步長=0.5

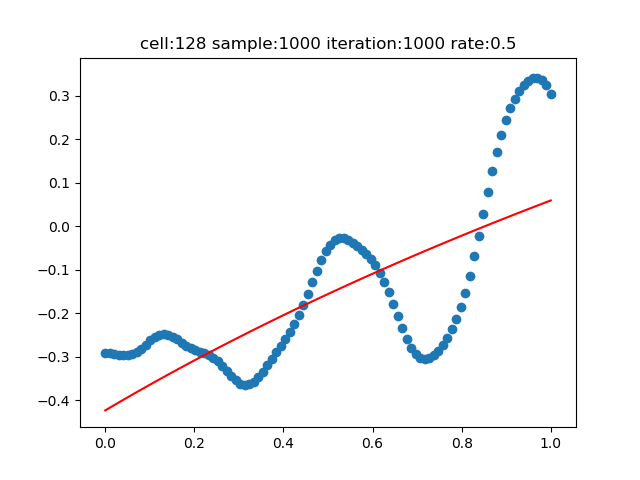
步長=0.01

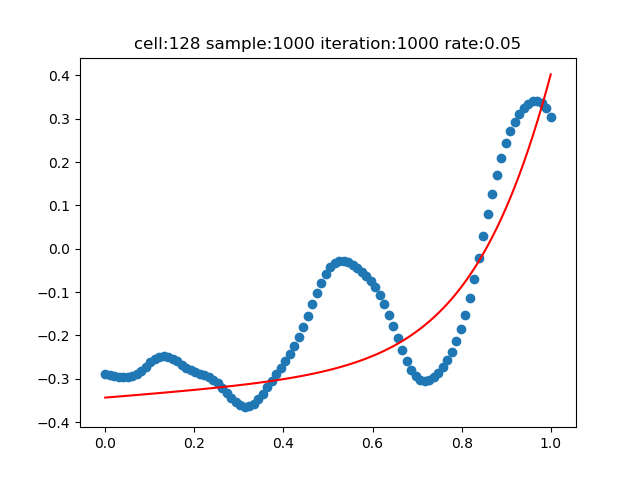
步長值太大或者太小，都會造成不好的效果。

總結如下（效果5分為最好）：

神經元數量	樣本量	迭代次數	步長值	效果
0	128	1000	1000	0.1	5
1	64	1000	2000	0.1	3
2	96	1000	1000	0.1	2.5
3	256	1000	500	0.1	0
4	128	500	1000	0.1	2
5	128	1500	1000	0.1	5
6	128	1000	500	0.1	2.5
7	128	1000	1500	0.1	5
8	128	1000	1000	0.5	1
9	128	1000	1000	0.05	2

兩層單入單出的神經網路能做什麼

定義神經網路結構

輸入層

權重矩陣W1/B1

隱藏層

權重矩陣W2/B2

輸出層

創造訓練資料

定義前向計算過程

定義代價函式

定義針對w和b的梯度函式

求W1的梯度

求B2的梯度

求W1的梯度

每次迭代後更新w,b的值

幫助函式

主程式初始化

程式主迴圈

測試並輸出擬合結果

引數調整

神經元數量的變化（標準值128）

樣本量的變化（標準值1000）

迭代次數的變化（標準值1000）

步長值的變化（標準值0.1）

相關推薦