BP神經網路中隱藏層節點個數的取值有下面幾種方法：

第一種方法：

一個經驗公式：

其中為隱藏層節點數目，為輸入層節點數目，為輸出層節點數目，為之間的調節常數。

第二種方法：

Kolmogorov定理確定隱藏層節點數：

柯爾莫哥洛夫(Kolmogorov)定理：

設 為一相互獨立的隨機變數序列，若滿足不等式

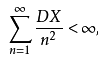
則服從強大數定律。

強大數定律可以表達為下式：

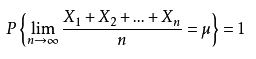
Kolmogorov定理說明給定任意連續對映F:[0,1] (n) →Rm可以精確地由一個三層前饋神經網路實現，第一層有n個神經元，第二層有2m+1個神經元，第三層有m個神經元。

Kolmogorov定理表明，隱層結點數為：

s＝2n＋1

其中n為輸入層結點數。

第三種方法：

論文：高大啟：有教師的線性基本函式前向三層神經網路結構研究

中指出的經驗公式：

其中m為輸入層節點數，n為輸出層節點數。