ACM-排列組合
話說排列組合博大精深,看來確實是的,各種駕馭不了的公式、定理啊!
組合,簡單的說就是從n個東西里面,挑出k個來,有多少種挑法。那麼,我們要如何方便的求出組合數c[n][k](代表從n個裡面取k個的不同方法)呢?據說楊輝三角可以解決!其實楊輝三角就是一堆有規律的數字,剛好它的規律就是二項式(a+b)^n展開後的係數,而這些係數也是有規律的,那就是二項式定理,剛好這個定理裡面就涉及到了組合數c[n][k]。倒推回去,意思就是說,我們可以根據楊輝三角算出組合數來。具體過程參考入門經典183頁,下面給出求組合數的程式碼:
#define MOD 10000 const int MAXN = 100; // 組合上限 int c[MAXN][MAXN]; // 組合數 void GetGroup() { c[0][0] = c[1][0] = c[1][1] = 1; for (int i=2; i<MAXN; ++i) { c[i][0] = 1; for (int j=1; j<=i; ++j) c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD; // 求模,防止結果過大 } return ; }
上面的程式就求出了C[MAXN][MAXN]以內的任意組合數,有點類似於打表。還有一點需要注意的就是,有些題目給出的資料比較大,如果取模對結果不影響的話,就可以在程式碼所示位置進行求模運算。
接下來,寫一道與組合有關的題吧,HDOJ:4810,時空轉移(點選開啟連結),題目如下:
Wall Painting
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1190 Accepted Submission(s): 334
Problem Description Ms.Fang loves painting very much. She paints GFW(Great Funny Wall) every day. Every day before painting, she produces a wonderful color of pigments by mixing water and some bags of pigments. On the K-th day, she will select K specific bags of pigments and mix them to get a color of pigments which she will use that day. When she mixes a bag of pigments with color A and a bag of pigments with color B, she will get pigments with color A xor B.
When she mixes two bags of pigments with the same color, she will get color zero for some strange reasons. Now, her husband Mr.Fang has no idea about which K bags of pigments Ms.Fang will select on the K-th day. He wonders the sum of the colors Ms.Fang will get with
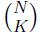
For example, assume n = 3, K = 2 and three bags of pigments with color 2, 1, 2. She can get color 3, 3, 0 with 3 different plans. In this instance, the answer Mr.Fang wants to get on the second day is 3 + 3 + 0 = 6.
Mr.Fang is so busy that he doesn’t want to spend too much time on it. Can you help him?
You should tell Mr.Fang the answer from the first day to the n-th day.
Input There are several test cases, please process till EOF.
For each test case, the first line contains a single integer N(1 <= N <= 103
Output For each test case, output N integers in a line representing the answers(mod 106 +3) from the first day to the n-th day.
Sample Input 4 1 2 10 1
Sample Output 14 36 30 8
題意:
給出n個數,並且也代表著總共有n天,第k天就從這n個數中選出k個數進行異或,然後將所有不同方案的異或值相加輸出即可。
分析:
要解決這道題,我們需要解決兩個問題,一是組合問題(很明顯的n選k),二是異或後相加問題。首先求組合數的問題,可以利用上面給出的方法,因為n最大為1000,可以先打表求出組合數;其次是異或,試想如果我們直接按照題目說的那樣,先求出各種組合,再直接異或,最後再相加求和,那得多麻煩啊,還不好寫,那有沒有其它的辦法呢?我們知道異或運算是位運算,並且規則是兩兩不同為一,否者為零,那麼根據這個性質,又可以得出一個等式:a xor b = x1<<(L-1) + x2<<(L-2) + ... + xj<<0(其中xj是a和b對應位的按位異或值,<<是左移運算,L為a和b的二進位制位數),其實就是對應位異或後乘上對應位的權重(2^j)。舉個例子:0001(1)xor 0010(2)= 0<<3 + 0<<2 + 1<<1 + 1<<0 = 3。也就是說,我們將整體上的異或拆成了對每一位上的運算。那我們這樣轉換有什麼用呢?其實,好處就是這樣改造異或運算後可以和組合聯絡起來,並且同時計算,就不用先求組合再求異或和了。如何聯絡?大家可以想象,將異或寫成了多項和的形式後,求異或就可以離散的求了,因為是多項的和,並且我們發現每一項都只與某一特定的二進位制位相關,那麼意味著可以對每一個二進位制位單獨討論後再求和,而對於單獨某一位的組合數,是不是就很好求了。所以,我們最終得出結論:ans = (c[a1][i]*c[b1][k-i])*(x1<<(L-1)) +(c[a2][k]*c[b2][k])*( x2<<(L-2)) + ... + (c[aj][k]*c[bj][k])*(xj<<0)(其中aj和bj分別代表對應位上1的個數和0的個數,因為只有1 xor 0才不為零,c[][]是組合數,k是第幾天)。最後一步就是如何求ai和bi了,其實只需要統計一下每一位上1的個數求出ai就行了,bi=n-ai。哦,對了,還有別忘了求模,資料可能會變得很大。
原始碼:
#include <cstdio>
#include <cstring>
#define MOD 1000003
#define LL long long
const int MAXN = 1003; // 組合上限
int c[MAXN][MAXN]; // 組合數
int num[MAXN], ans[MAXN];
void GetGroup ()
{
c[0][0] = c[1][0] = c[1][1] = 1;
for (int i = 2; i < MAXN; i++)
{
c[i][0] = 1;
for (int j=1; j<=i; ++j)
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD;
}
return ;
}
void func (int data) // 統計每一位上1的個數
{
for (int i=0; i<32; ++i)
if (data & (1<<i))
++num[i];
}
int main ()
{
int n;
GetGroup ();
while(~scanf ("%d", &n))
{
int tmp;
memset (num, 0, sizeof(num));
memset (ans, 0, sizeof(ans));
for (int i=0; i<n; ++i)
{
scanf("%d", &tmp);
func(tmp);
}
for(int k=1; k<=n; ++k) // 根據推出的結論算出每天對應的答案
for(int j=0; j<32; ++j)
for(int i=1; i<=num[j]&&i<=k; i+=2)
ans[k] = (ans[k]+(LL)c[num[j]][i]*c[n-num[j]][k-i]%MOD*(1<<j)%MOD)%MOD;
for(int k=1; k<=n; ++k)
printf("%d%c", ans[k], k==n ? '\n' : ' ');
}
return 0;
}
關於組合數就先說到這吧,後面有了新東西再過來補充,其它類似的題目還有,HDOJ:4045。
