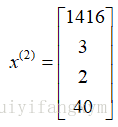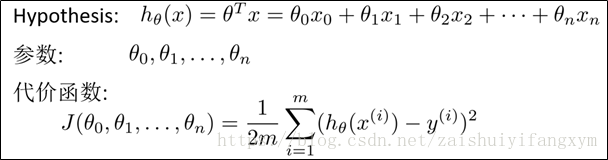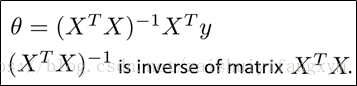吳恩達(Andrew Ng)《機器學習》課程筆記(2)第2周——多變數線性迴歸
目錄
四、多變數線性迴歸(Linear Regression with multiple variables)
4.1. 多維特徵(Multiple features)
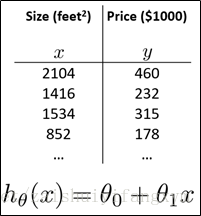
前面介紹的是單變數線性迴歸如下圖所示:
現在介紹多變數線性迴歸,有多個輸入變數x,一個輸出變數y。
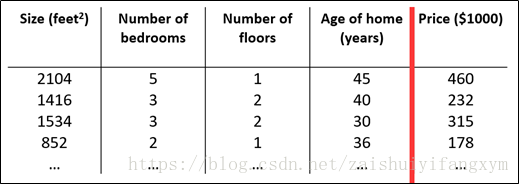
例如,下圖所示的房屋尺寸,數量等構成多個特徵。
增加新的特徵後,要引入新的註釋:
n代表特徵向量的數量;
在矩陣中代表第i行。例如:
在矩陣中表示第i行第j個特徵;例如
知道了上面後,多變數假設h表示為:
為了簡化公式,引入,則公式轉化為:
其中,x,θ分別表示為:
4.2. 多變數梯度下降(Gradient descent for multiple variables)
與單變數線性迴歸類似,在多變數線性迴歸中,我們也構建一個代價函式(cost function)。
我們的目標和單變數線性迴歸問題一樣,要找出使得代價函式最小的引數。
多變數線性迴歸的批量梯度下降演算法為:
求導可得出:
n=1,單變數(一維特徵)
n>=1,多變數(多維特徵)
最開始隨機選擇一系列的引數值,計算所有的預測結果,再給所有的引數一個新的值,不斷迭代迴圈,直到收斂為止。
4.3. 梯度下降法實踐1——特徵縮放(Feature Scaling)(歸一化)
多維特徵,我們要保證這些特徵具有相近的尺度,這樣使得梯度下降演算法收斂更快。
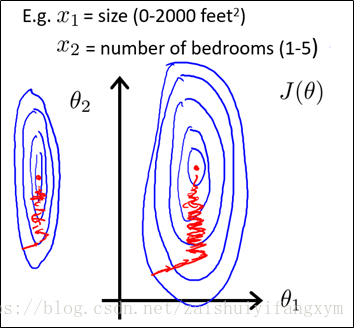
以房價問題為例,假設兩個特徵,房屋的尺寸和房屋的數量,尺寸的值在0-2000,而房間數量的範圍在0-5,很顯然,兩個特徵的差距很大。以兩個引數分別為橫縱座標,繪製代價函式的等高線圖,影象看起來很扁,這樣,在梯度下降演算法中,需要迭代迴圈很多次才能收斂,這樣時間會大大增加。
特徵之間差距很大這將使得演算法迭代次數變多,圖中紅色代表收斂的次數。
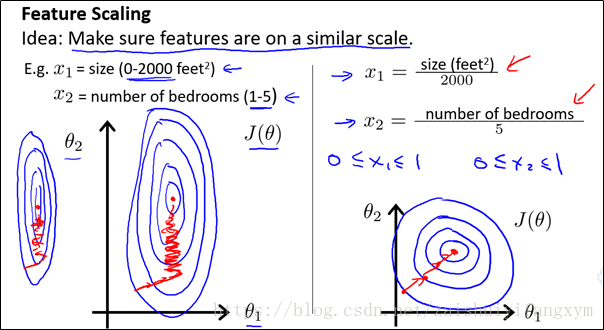
所以,解決的方式,是將所有特徵儘量縮放到一個區間範圍內。如(-1,1)之間。
如下圖所示,為一種縮放方法,使得特徵縮放到(0,1)區間內。這樣等高線圖變得圓一些。收斂次數將減少。
特徵縮放區別選擇,有很多(-1,1),(0,1),(0,3)……,但區間範圍不能太大或太小。這樣也會影響收斂次數。
例如:均值歸一化,使得特徵縮放到(-0.5,0.5)區間內;
均值歸一化公式如下:
有了特徵縮放,在梯度下降法中,收斂次數將大大減少,速度將變得更快。
4.4. 梯度下降法實踐2——學習率(Learning rate)
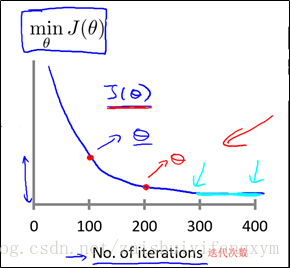
不同的資料,在梯度下降法收斂所需要的迭代次數將不同,當然,迭代次數我們不可預知。我們大概繪製出迭代次數和代價函式的趨勢圖來觀測演算法在什麼時候收斂。
梯度下降法的每次迭代次數受學習率α影響。正如前面一節所說,如果學習率α過小,則收斂所需的迭代次數會很高;如果學習率α過大,則每次地帶可能不會使代價函式減少,可能會超過區域性最小值區間,導致無法收斂。
4.5. 特徵和多項式迴歸(Features and polynomial regression)
以房屋價格為例,如上圖所示:
其中,=frontage(臨街寬度),
=depth(深度),
= frontage × depth =area (房屋面積),
房屋價格問題轉化為:
使得,房屋價格從多元變數線性問題轉化為單變數線性問題,這樣可以簡化演算法的複雜度。 其實,並不是線性問題適合所有的資料。有時候,我們需要曲線(多項式)來解決問題。
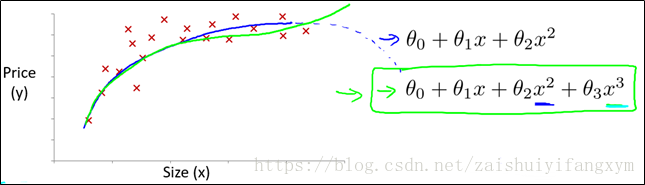
例如,下圖是房屋價格的資料,如果用直線,去擬合,當然可以。但是用多項式模型,模型預測的資料將會更接近。
如下圖,對於上圖的資料,如果用二次方模型,最後趨勢(藍色線)將呈現下降趨勢,很顯然這不符合客觀規律,因為房屋價格會隨著房屋大小增大而增大,整體應呈現上升趨勢。若用,三次方模型,則趨勢(綠色線)呈現上升趨勢,並且資料擬合的較好。所以,對於這個資料,用三次方模型更合適。
一般情況,拿到資料,通常我們需要將先觀察的資料,再決定用什麼模型。另外我麼可以令:
從而將模型轉化為線性迴歸模型。
根據函式特性,可以使:
或者使用下面的模型:
值得注意的是:採用多項式迴歸模型,在執行梯度下降演算法前,多維特徵必須要進行特徵縮放(歸一化),使每個特徵放到一個區間範圍內。
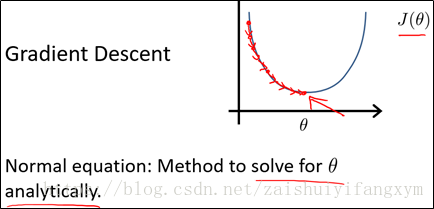
4.6. 正規方程(Normal equation)
目前為止,我們僅僅學習梯度下降法,但對某些線性迴歸問題,正規方程法求解會更好,下面將介紹正規方程法解決線性迴歸問題。
如上圖所示,梯度下降法將不斷迭代,直到收斂;正規方程與此不同,正規方程將一次就可以找到最優解。下面給出利用正規方程求解得到最小引數θ :
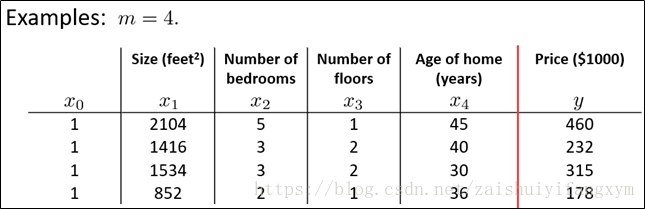
下面舉個例子進行說明:
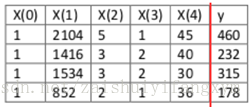
如上面的表格所示,房屋的四維特徵對應最後的房屋價格。利用正規方程的解以此為求出:
由公式可得出:
最後,使得代價函式最小的最優解可以一次得到,相比於梯度下降法簡單得多。在Octave或Matlab程式中,一句話就可以解決:
Octave/Matlab: pinv(X’*X)*X’*y
注:對於不可逆矩陣,正規方程不可以用。
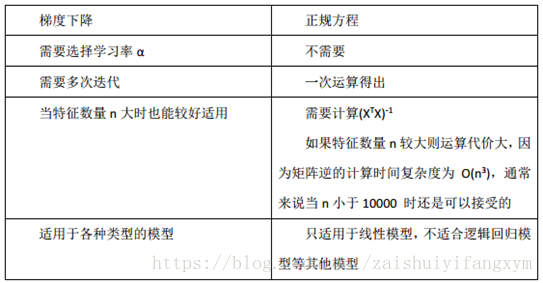
下面將梯度下降法和正規方程法進行比較:
總之,只要特徵變數數目不太大(小於1萬),通常使用正規方程法,而不是用梯度下降法。
後面,我們要學習分類演算法,如邏輯迴歸演算法,並不能使用正規方程法,對於複雜的學習演算法,我們將不得不使用梯度下降法求解。因此梯度下降法可以在大量多維特徵變數的線性迴歸問題。
五、Octave 教程
Octave最初是模彷Matlab而設計,語法基本上與Matlab一致,嚴謹編寫的程式碼應同時可在Matlab及Octave執行,但也有很多細節上差別。一些軟體開發小組也使用兩者相容的語法,直接開發可以同時在Matlab和Octave使用的程式。所以直接用Matlab就行了,我自己安裝的是Matlab R2017b版本。
Matlab 一些基本操作可以看我的部落格,比較簡單,容易上手。
其他的操作比較簡單,下面的內容直接省略。需要的可以查閱書籍:《MATLAB R2016a完全自學一本通》
5.1. 基本操作(Basic Operations)
5.2. 移動資料(Moving Data Around)
5.3. 計算資料(Computing on Data)
5.4. 繪圖資料(Plotting Data)
5.5. 控制語句:for,while,if語句(Control Statements_ for, while, if statements)
5.6. 向量化(Vectorization)
參考資料
[1] Andrew Ng Coursera 機器學習 第二週 PPT