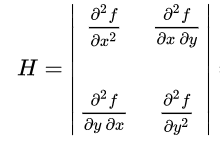前言

1、看了關於牛頓法相關的文章，下面是總結記錄。

2、感受的話：數學公式最為重要的是數學符號語言的理解，如果第一次看不懂很正常，保持住心態最為重要，然後將每個符號帶入公式和公式描述語言裡就能理解，還有一篇看不懂就看第二篇，第三篇....(ps:我是捏著鼻子看完又臭又長的公式)

必備知識點：

1、泰勒級數展開式

(ps:這個要記下來，不要問為什麼)

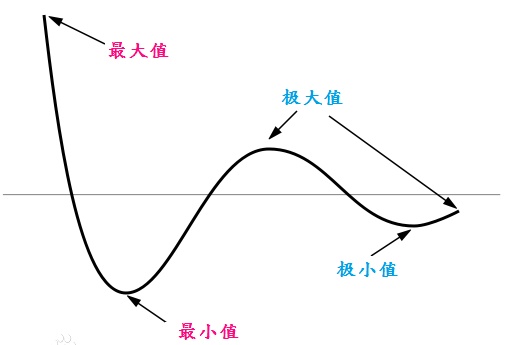
2、極值點

對任意的函式f(x)的一階導為0時，該點一定是極值點。

這裡假設我們要求的值是Xt,其估計值為Xk,這裡一定要注意，有了估計值，要通過牛頓法來逼近Xt.

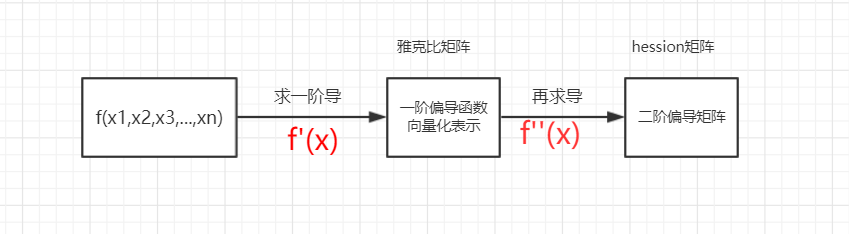
3、雅克比矩陣(Jacobian)：

在向量分析中，雅可比矩陣是函式的一階偏導數以一定方式排列成的矩陣，其行列式稱為雅可比行列式。
 

翻譯如下：

就是由多元函式的一階偏導函式構成的一維向量

4、海森矩陣（Hessian matrix 或 Hessian）

是一個多變數實值函式的二階偏導陣列成的方塊矩陣

翻譯如下：

由多元函式的各個變數的二階偏導構成的，是對雅克比向量再求導的結果。

（就是對一坨一維向量再求導後就是這麼個一坨矩陣）

關係歸納：

公式推導：

(這裡我直接借用了第三篇文章中的截圖)

這裡我在關鍵處做了筆記。

由1式到2式沒什麼可說的，捨棄泰勒級數後的最小項，對2式求導得到3式是關鍵。

1、f(x)求導，這裡的求導一定是指對x求導，所以2式中x最高次項就是x的平方項。
2、對於已知f(x)，一階導f'(x)可以寫出來表示式。
3、f(x)=ax+b 如果a,b為常數,則f'(x)=a.
4、對於已知X=Xk,帶入一階導和二階導中，值可以計算出來的，是個常數項，不會參與泰勒級數展開式的等號左右兩項的求導中
 

這樣再來看由2式到3式，原文的作者已經寫得很清晰了。一開始最為頭疼就是怎麼會出來個f''(Xk)這個玩意兒，其實就是f(Xk)的二階導而已，是個常數項，照抄就行。

到上面為止，我們只能說到了一維能理解了。也就是第3篇作者所說n=1，就是一維空間。也是在高數中的常見知識點。

N維空間

(這裡我依然用截圖)

雅克比矩陣說明

一階導明確求導變數，其餘看成常量，所以一階導的向量化表示無壓力看明白(ps:看官若有不明白之處請自行問度娘)。到二階導我是一度暈厥過去。

Hession矩陣的說明

二元函式的Hession矩陣：

多元函式的Hession矩陣：

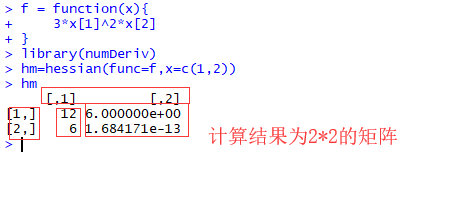
我又參考了第2篇文章中的說明，和R程式碼的計算結果，理解二元的了，然後進而推廣理解了多元的情況。

(ps:我自己下載了R和RStudio驗證了程式碼)

程式碼說明：

(關於程式碼說明此處只能給出簡單的雅克比和海森矩陣的說明,也就是第2篇中的程式碼說明，第一篇有部分程式碼我沒看明白)

1、雅克比矩陣計算：

2、海森矩陣計算：

最後部分：

公式推導的最後，在理解了雅克比和海森矩陣後，剩餘部分都是符號計算和一維的情況一樣，所以沒什麼難理解的，難以計算，這也恰是其一個缺點。(ps:看官可自己看第3篇剩餘部分）

結束語：

演算法公式看的著重點是對每個符號的含義把握住，帶入到公式中看，其實沒有你想的那麼難，數學家為了好表達(就是少碼字!!!!),就借用一大推的表示符號。

(ps:這裡沒有對第一篇參考文章做說明，解釋，寫不動了，臥槽，快凌晨兩點了，明天還上班)

參考文章說明

第1/2兩篇說明

第1、2兩篇是關於R實現的，並舉例說明的，我簡單把程式碼拷貝到R studio中運行了，很直觀，特別是第二篇，臥槽，茅塞頓開。

第3篇說明

第3篇是又臭又長的數學公式文章，MD我第一邊看的時候就想罵娘，能不能說人話，不過自己翻譯之後，還是很感謝作者的

參考文章：

3、牛頓法