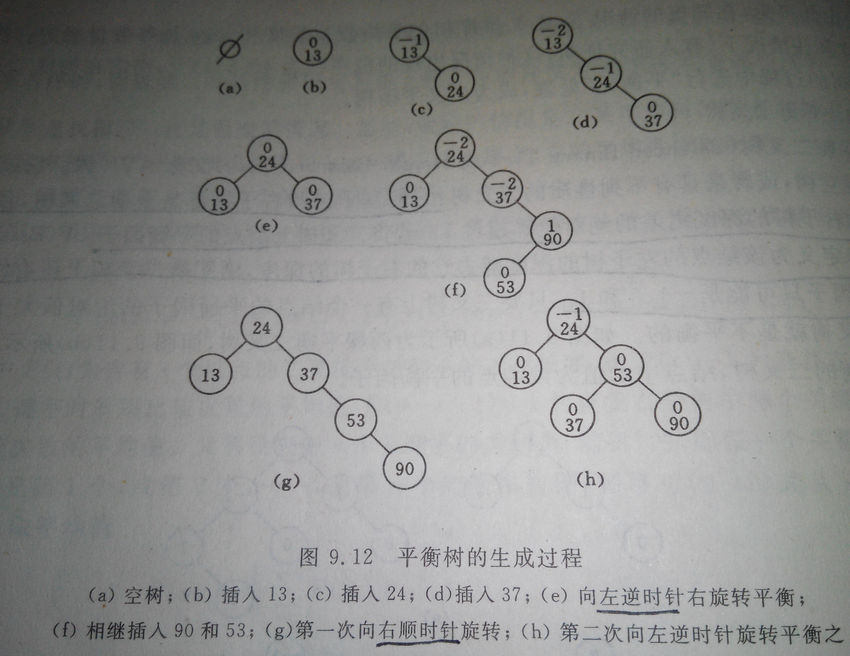
平衡二叉樹（Balanced Binary Tree）又被稱為AVL樹（有別於AVL演算法），且具有以下性質：它是一 棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。構造與調整方法 平衡二叉樹的常用演算法有紅黑樹、AVL、Treap等。 最小二叉平衡樹的節點的公式如下 F(n)=F(n-1)+F(n-2)+1 這個類似於一個遞迴的數列，可以參考Fibonacci數列，1是根節點，F(n-1)是左子樹的節點數量，F(n-2)是右子樹的節點數量。
      AVL是最先發明的自平衡二叉查詢樹演算法。在AVL中任何節點的兩個兒子子樹的高度最大差別為一，所以它也被稱為高度平衡樹，n個結點的AVL樹最大深度約1.44log2n。查詢、插入和刪除在平均和最壞情況下都是O（log n）。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。
      如何生成一個二叉樹呢，我們可以來看看下面這一幅圖：
 

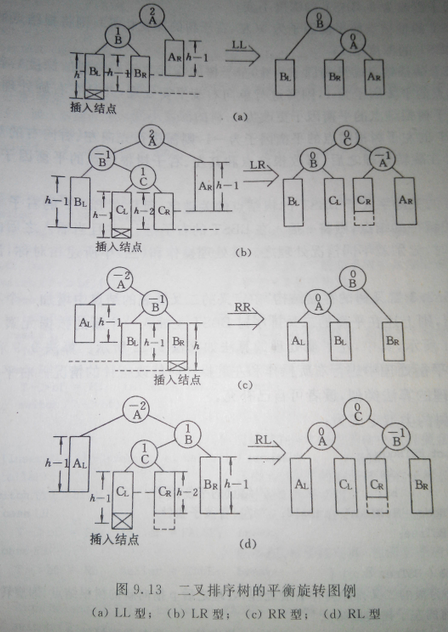
      一般情況下，假設由於在二叉排序樹上插入結點而失去平衡的最小子樹根結點的指標為a(即a是)離插入結點最近，且平衡因子絕對值超過1的祖先結點），則失去平衡後進行的調整規律有四種：
      （1）**單向右旋平衡處理**；
          使用在插入結點位置為*a的**左子樹根結點的左子樹**，且樹失去平衡。

      （2）**單向左旋平衡處理**；
            使用在插入結點位置為*a的**右子樹根結點的右子樹**，且樹失去平衡。

      （3）**雙向旋轉（先左後右）平衡處理**；
      使用在插入結點位置為*a的**左子樹根結點的右子樹**，且樹失去平衡。

      （4）**雙向旋轉（先右後左）平衡處理**；
            使用在插入結點位置為*a的**右子樹根結點的左子樹**，且樹失去平衡。

           下面**有圖有真相**
 

下面顯示程式程式碼：
功能有：
（1）插入陣列中的元素生成AVL樹。
（2）中序遍歷AVL樹得到正序資料。
（3）查詢是否AVL樹中是否存在要求的關鍵字。
（4）不存在要求的關鍵字的時候選擇是否插入關鍵字到AVL樹中。
（5）中序遍歷新的AVL樹。

#include<iostream>
#include<stdlib.h>
using namespace std;

//測試元素數量
#define N 5

//定義平衡狀態
#define LH 1
#define EH 0
#define RH -1
#define
 
 TRUE 1
#define FALSE 0

//比較
#define EQ(a,b) ((a)==(b))
#define LT(a,b) ((a)<(b))
#define RT(a,b) ((a)>(b))


//資料元素型別定義
struct ElemType
{
    int key;
    int order;
};

//AVL樹的定義
typedef struct AVLNode
{
    ElemType data;
    int bf;         //結點的平衡因子
    struct AVLNode *lchild,*rchild;     //左右孩子指標
}AVLNode,*AVLTree;



//下面是AVL樹常用操作

//單右旋處理
void R_Rotate(AVLTree &p)
{
    //對以*p為根的二叉排序樹做右旋處理，處理後p指向新的樹根節點，即旋轉處理之前的左子樹的根節點
    AVLTree lc;
    lc=p->lchild;           //lc指向*p的左子樹根節點
    p->lchild=lc->rchild;   //lc的右子樹掛接為*p的左子樹
    lc->rchild=p;
    p=lc;  //p指向新的根結點
}

//單左旋處理
void L_Rotate(AVLTree &p)
{
    //對以*p為根的二叉排序樹做左旋處理，處理後p指向新的樹根節點，即旋轉處理之前的右子樹的根節點
    AVLTree rc;
    rc=p->rchild;           //rc指向*p的右子樹根節點
    p->rchild=rc->lchild;   //lc的左子樹掛接為*p的右子樹
    rc->lchild=p;
    p=rc;  //p指向新的根結點
}

//左平衡旋轉處理
void LeftBalance (AVLTree &T)
{
    //對以指標T所指結點為根的二叉樹做左平衡旋轉處理，演算法結束後，指標T指向新的根節點
    AVLTree lc,rd;
    lc=T->lchild;           //lc指向*T的左子樹根節點
    switch (lc->bf)
    {
    case LH:                //新結點插入在*T的左孩子的左子樹上，要做單右旋處理。
        T->bf=lc->bf=EH;
        R_Rotate(T);break;  
    case RH:                //新結點插入在*T的左孩子的右子樹上，要做雙旋處理
        rd=lc->rchild;      //rd指向*T的左孩子的右子樹根
        switch (rd->bf)
        {
            //修改*T及其左孩子的平衡因子
        case LH:
            T->bf=RH;
            lc->bf=EH;
            break;
        case EH:
            T->bf=lc->bf=EH;
            break;
        case RH:
            T->bf=EH;
            lc->bf=LH;
            break;

        default:
            break;
        }
        //rd->bf=EH;
        L_Rotate(T->lchild);    //  對*T的左子樹做左旋平衡處理
        R_Rotate(T);            //  對*T做右旋平衡處理

    default:
        break;
    }

}

//右平衡旋轉處理
void RightBalance (AVLTree &T)
{
    //對以指標T所指結點為根的二叉樹做右平衡旋轉處理，演算法結束後，指標T指向新的根節點
    AVLTree rc,rd;
    rc=T->rchild;           //rc指向*T的右子樹根節點
    switch (rc->bf)
    {
    case RH:                //新結點插入在*T的右孩子的右子樹上，要做單左旋處理。
        T->bf=rc->bf=EH;
        L_Rotate(T);break;  
    case LH:                //新結點插入在*T的右孩子的左子樹上，要做雙旋處理
        rd=rc->lchild;      //rd指向*T的右孩子的左子樹根
        switch (rd->bf)
        {
            //修改*T及其右孩子的平衡因子
        case LH:
            T->bf=EH;
            rc->bf=RH;
            break;
        case EH:
            T->bf=rc->bf=EH;
            break;
        case RH:
            T->bf=LH;
            rc->bf=EH;
            break;

        default:
            break;
        }
        rd->bf=EH;
        R_Rotate(T->rchild);    //對*T的右子樹做右旋平衡處理
        L_Rotate(T);            //  對*T做左旋平衡處理
    default:
        break;
    }


}

//插入操作
int InsertAVL(AVLTree &T,ElemType e,bool &taller)
{
    //若在平衡的二叉排序樹T中不存在和e有相同關鍵字的結點，則插入一個數據元素
    //為e的新結點，並返回1，否則返回0.若因插入而使二叉排序樹失去平衡，則做平衡二叉樹
    //旋轉處理，布林變數taller反映T長高與否

    if(!T)
    {
        //插入新結點，樹長高，置taller為TRUE
        T=(AVLTree)malloc(sizeof(AVLNode));
        T->data=e;
        T->lchild=T->rchild=NULL;
        T->bf=EH;
        taller=TRUE;
    }
    else
    {
        if(EQ(e.key,T->data.key ))      //樹中已經存在和e相同關鍵字的結點
        {
            taller=FALSE;  
            return 0;                   //跳出程式，不再插入
        }
        else if(LT (e.key,T->data.key))  //在左子樹尋找
        {
            if(!InsertAVL(T->lchild,e,taller))      return 0;   //遞迴呼叫插入函式，無插入則跳出
            if(taller)                  //  已插入到*T的左子樹中且左子樹“增高”
                switch(T->bf)           //  檢查*T的平衡度
                {
                case LH:                //  原本左子樹比右子樹高，需要做左平衡處理
                    LeftBalance(T);taller =FALSE; break;
                case EH:                //  原本左右子樹等高，現在因為左子樹增高而使樹增高
                    T->bf=LH; taller=TRUE;break;
                case RH:                //  原本右子樹比左子樹高，現在左右子樹等高
                    T->bf=EH;
                    taller=FALSE;
                }
        }
        else
        {
            if(!InsertAVL(T->rchild,e,taller))      return 0;   //遞迴呼叫插入函式
            if(taller)              //  已插入到*T的左子樹中且左子樹“增高”
                switch(T->bf)       // 檢查*T的平衡度
                {
                case LH:            //  原本左子樹比右子樹高，現在左右子樹等高
                    T->bf=EH;
                    taller=FALSE;
                case EH:            //  原本左右子樹等高，現在因為右子樹增高而使樹增高
                    T->bf=RH; taller=TRUE;break;
                case RH:            //  原本右子樹比左子樹高，現在做右平衡處理
                    RightBalance(T);taller =FALSE; break;
                }
        }
    }
    return TRUE;
}
//visit 函式
void visit(ElemType e)
{
    cout<<"( "<< e.key<<", "<<e.order<<" )   ";
}

//中序遍歷二叉樹
void InOrderTraverse(AVLTree T,void(*visit)(ElemType e))
{
    //二叉樹存在;visit函式是對結點進行操作
    //對二叉樹進行先序遍歷，每一個結點有且只有一次呼叫visit
    if(T)                                           //樹非空
    {
        InOrderTraverse(T->lchild,visit);           //對左子樹進行遍歷
        visit(T->data);
        InOrderTraverse(T->rchild,visit);           //對右子樹進行遍歷
    }

}
//查詢關鍵字
int searchAVL(AVLTree &T,int key)
{
    //AVLTree p,f;
    if(!T)
    {
        char i;
        bool k;
        cout<<"沒有此關鍵字"<<endl;
        cout<<"是否需要插入此關鍵字進AVL？(Y/N)"<<endl;
        cin>>i;
        if(i==89||i==121)
        {
            ElemType temp;
            temp.key=key;
            temp.order=N+1;
            InsertAVL(T,temp,k);
        }

        return FALSE;
    }
    else if(EQ(key,T->data.key))
        cout<<"( "<< T->data.key<<", "<<T->data.order<<" )   "<<endl;
    else if(LT(key,T->data.key))
        searchAVL(T->lchild,key);
    else
        searchAVL(T->rchild,key);
}
//初始化空樹(構造空樹)
void InitAVL(AVLTree &T)
{
    T=NULL;
}

int main()
{
    AVLTree at;
    int i,j;
    bool k;
    ElemType e[N]={{13,1},{24,2},{37,3},{90,4},{53,5}};
    InitAVL(at);
    for(i=0;i<N;i++)
    {
        InsertAVL(at,e[i],k);
    }
    InOrderTraverse(at,visit);
    //PreOrderTraverse(at,visit);
    cout<<endl;
    cout<<"請輸入要尋找的關鍵字"<<endl;
    cin>>j;
    searchAVL(at,j);
    cout<<"重新中序遍歷"<<endl;
    InOrderTraverse(at,visit);
    cout<<endl;
    system("pause");
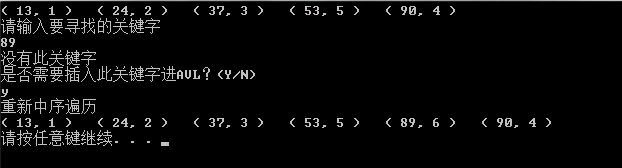
    return 0;
}

結果截圖

這裡程式碼參考的是上面一幅圖——平衡樹生成過程的陣列。
ps:這裡只是講到AVL樹的生成插入過程，刪除操作下回細說。