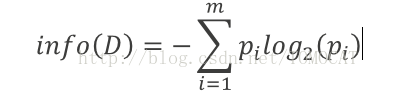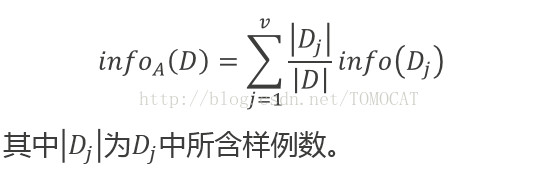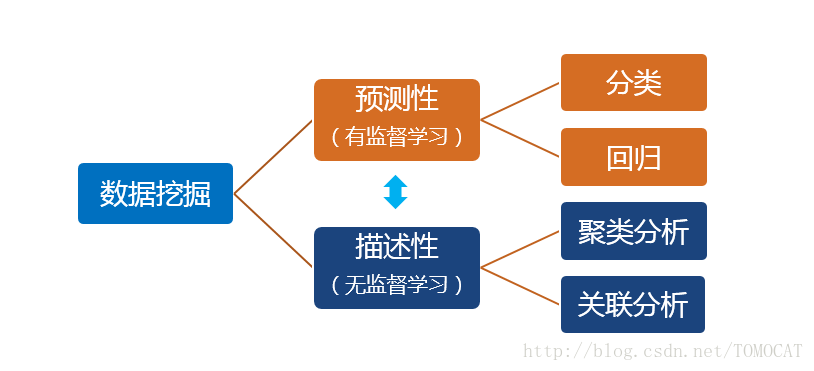
一、資料探勘任務分類

1、預測性和描述性的主要區別在於是否有目標變數

2、預測性包括分類和迴歸：

（1）分類：輸出變數為離散型，常見的演算法包括（樸素）貝葉斯、決策樹、邏輯迴歸、KNN、SVM、神經網路、隨機森林。

（2）迴歸：輸出變數為連續型。

3、描述性包括聚類和關聯：

（1）聚類：實現對樣本的細分，使得同組內的樣本特徵較為相似，不同組的樣本特徵差異較大。例如零售客戶細分。

（2）關聯：:指的是我們想發現數據的各部分之間的聯絡和規則。常指購物籃分析，即消費者常常會同時購買哪些產品，從而有助於商家的捆綁銷售。

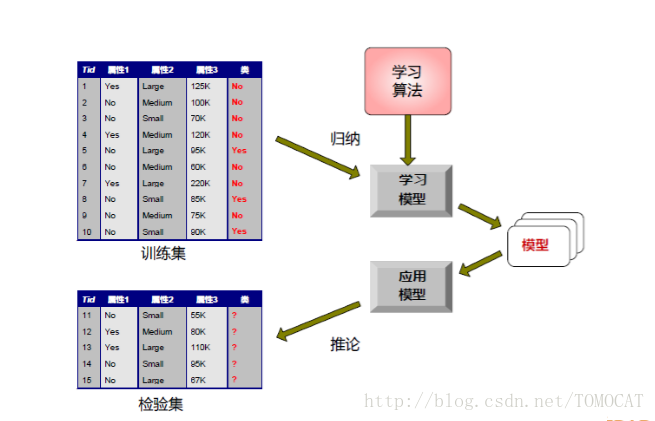
4、建立分類模型的一般方法：

二、樸素貝葉斯

1、貝葉斯定理：

2、原理：

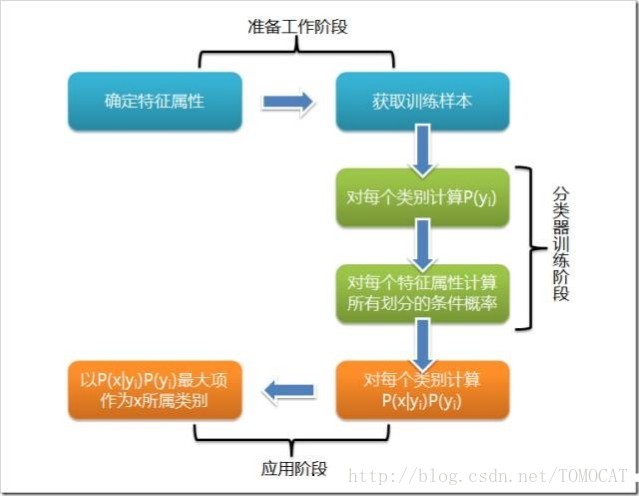
3、樸素貝葉斯分類流程

三、決策樹

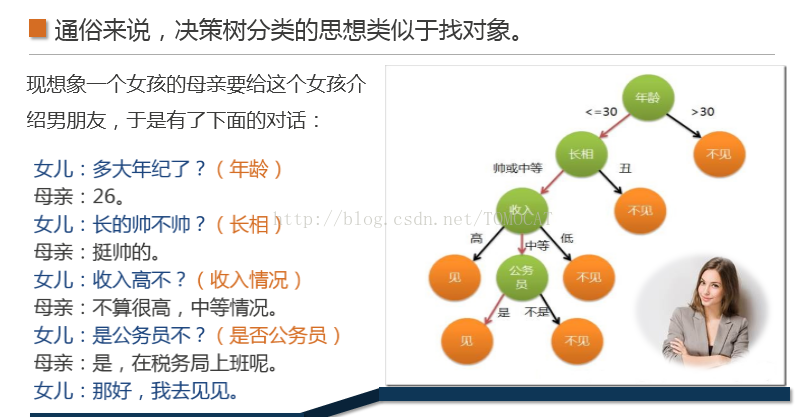
1、原理，相當於找物件

2、決策樹定義：

決策樹（DecisionTree）是一個樹結構（可以是二叉樹或非二叉樹）。其每個非葉節點表示一個特徵屬性上的測試，每個分支代表這個特徵屬性在某個值域上的輸出，而每個葉節點存放一個類別。使用決策樹進行決策的過程就是從根節點開始，測試待分類項中相應的特徵屬性，並按照其值選擇輸出分支，直到到達葉子節點，將葉子節點存放的類別作為決策結果。

其中屬性選擇度量的演算法很多，一般使用自頂向下遞迴分治法，並採用不回溯的貪心策略。ID3和C4.5是兩種常用演算法。

4、ID3演算法：

資訊增益是特徵選擇中的一個重要指標，它定義為一個特徵能夠為分類系統帶來多少資訊，帶來的資訊越多，該特徵越重要。

基本資訊包括：熵，期望資訊和資訊增益。

（1）熵：設D為用類別對訓練元組進行的劃分，則D的熵表示為：

其中?i表示第i個類別在整個訓練元組中出現的概率，可以用屬於此類別元素的數量除以訓練元組元素總數量作為估計。熵的實際意義表示是D中元組的類標號所需要的平均資訊量。

（2）期望資訊：

現在我們假設將訓練元組D按屬性A進行劃分，則A對D劃分的期望資訊為：

（3）資訊增益：

（4）待補充案例：SNS社群中不真實賬號檢測的例子如中使用ID3演算法構造決策樹。

5、C4.5演算法：

（1）ID3演算法存在的問題：偏向於多值屬性，例如，如果存在唯一標識屬性ID，則ID3會選擇它作為分裂屬性，這樣雖然使得劃分充分純淨，但這種劃分對分類幾乎毫無用處。（例如會選擇主鍵）

四、邏輯迴歸

1、原理：