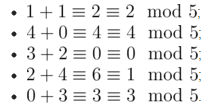A. Lucky Permutation Triple time limit per test 2 seconds memory limit per test 256 megabytes input standard input output standard output

Bike is interested in permutations. A permutation of length n is an integer sequence such that each integer from 0 to (n - 1) appears exactly once in it. For example, [0, 2, 1] is a permutation of length 3 while both [0, 2, 2] and [1, 2, 3] is not.

A permutation triple of permutations of length n (a

, b, c) is called a Lucky Permutation Triple if and only if . The sign a_i denotes the i-th element of permutation a. The modular equality described above denotes that the remainders after dividing a_i + b_i by n and dividing c_i by n are equal.

Now, he has an integer n and wants to find a Lucky Permutation Triple. Could you please help him?

Input

The first line contains a single integer n (1 ≤ n ≤ 10⁵).

Output

If no Lucky Permutation Triple of length n exists print -1.

Otherwise, you need to print three lines. Each line contains n space-seperated integers. The first line must contain permutation a, the second line — permutation b

, the third — permutation c.

If there are multiple solutions, print any of them.

Sample test(s) input

5

output

1 4 3 2 0
1 0 2 4 3
2 4 0 1 3

input

2

output

-1

Note

In Sample 1, the permutation triple ([1, 4, 3, 2, 0], [1, 0, 2, 4, 3], [2, 4, 0, 1, 3]) is Lucky Permutation Triple, as following holds:

In Sample 2, you can easily notice that no lucky permutation triple exists.

若n為偶數則無解 否則a和b都為0..n-1,c求出來正好是全排列

#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cstring>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<=n;i++)
#define Forp(x) for(int p=pre[x];p;p=next[p])
int main()
{
//	freopen(".in","r",stdin);
// 	freopen(".out","w",stdout);
    int n;
    cin>>n;
    if (n%2==0) puts("-1");
    else
    {
        Rep(i,n-2) cout<<i<<' ';cout<<n-1<<endl;
        Rep(i,n-2) cout<<i<<' ';cout<<n-1<<endl;
        Rep(i,n-2) cout<<(2*i)%n<<' ';cout<<(2*n-2)%n<<endl;
    }


	return 0;
}