2. 程式人生 > >【演算法導論】B樹

【演算法導論】B樹

阿新 • • 發佈：2019-02-19

      一棵B樹T是具有如下性質的有根樹（設根為root）:

1.每個節點x有一下域：

  （a）num,當前儲存在節點x的關鍵字個數,關鍵字以非降序存放，因此key[i]<=key[i+1]<=……key[n]；

  （b）isleaf,是一個bool值，如果x為葉子節點，則isleaf=true.

  （c）每個節點包括num+1個指向其子女的指標p[0],p[1],……p[num]。如果x為葉子，則p=NULL

  （d）每個節點包括num個關鍵字key[0],key[1],……key[num-1]。各關鍵字key[i]對儲存在各子樹中的關鍵字範圍加以分隔：  k1<=key[1]<=k2<=key[2]……

2.每個葉節點具有相同的深度。

3.每一個節點包含的關鍵字有上下界。這些界可以用一個稱為B樹的最小度數的固定整數M>=2來表示。每個非根節點的個數n必須滿足M-1<=n<=2M-1。根節點至少包括    一個關鍵字。如果一個節點是滿的，則它恰好有2M-1個關鍵字。

       一棵B樹可以表示如下：


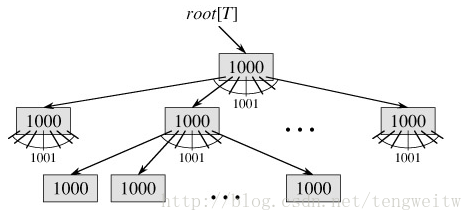
        B樹與紅黑樹的相似之處在於，每棵有n個節點的B樹高度為O（lgn），但可能要比一棵紅黑樹的高度小很多，因為它的分支比較多！因為在磁碟儲存中，需要經常讀取資料，所以選擇一個大的分支因子，可以大大地降低樹的高度，以及磁碟存取次數。這樣說可能比較抽象，下面舉例說明：下圖為一棵分支因子為1001、高度為2的B樹，可以看出它可以儲存超過10億個關鍵字；但是，因為根節點可以持久的保留在主存中，因此需找某個關鍵字至多隻需要兩次磁碟存取。如果用二叉樹儲存的話，樹的深度將會很大，那麼尋找位於葉子節點處的關鍵字將需要很多次磁碟讀取！假設有n個節點，那麼二叉樹的高度為h<=lg(n+1),而B樹為h<=log((n+1)/2)/log(M),其中M為最小度數。


B樹的各種操作：

1.查詢

    查詢b樹和查詢二叉樹類似，就是在分支處進行判斷選擇正確的子樹，然後遞迴呼叫。查詢過程的時間複雜讀為Mlgn/lgM具體程式實現如下：

/**********************************************************\
函式功能：查詢關鍵字所在的節點
輸入：    樹的根，關鍵字
輸出：    關鍵字所在的節點
\**********************************************************/
BtreeNode *BtreeSearch(BtreeNode *TestNode,int keyword)
{
	int i=0;
	while(i<TestNode->num&&keyword>TestNode->key[i])
		i=i+1;
	if(i<=TestNode->num&&keyword==TestNode->key[i])
		return TestNode;
	if(TestNode->isleaf)
	{
		printf("Not founded!\n");
		return NULL;
	}
	else
	{
		return BtreeSearch(TestNode->p[i],keyword);
	}
}

2.建立空的B樹

/**********************************************************\
函式功能：建立節點
輸入：無
輸出：新節點
\**********************************************************/
BtreeNode * BtreeCreate()
{
	BtreeNode *node=(BtreeNode *)malloc(sizeof(BtreeNode));
	if(NULL==node)
		return NULL;
	node->isleaf=true;
	node->num=0;
	for(int i=0;i<2*M;i++)
		node->p[i]=NULL;
	for(int i=0;i<2*M-1;i++)
		node->key[i]=0;
	return node;
}

3.插入

        B樹的插入比二叉樹的插入要複雜的多，因為二叉樹的插入是插入新的節點，而B樹的插入是將關鍵字插入到已存在的節點，而節點可能已經是滿節點（前面提到過），就會破壞B樹的性質。因此不能將關鍵字插入到滿節點上。根據B樹的規則，每個節點的關鍵字個數在[M-1, 2M-1]之間，故當keyword(要插入的關鍵字)要加入到某個葉子時，如果該葉子節點已經有2M-1個關鍵字，則再加入keyword就違反了B樹的定義，這時就需要對該葉子節點進行分裂，將葉子以中間節點為界，分成兩個包含M-1個關鍵字的子節點，同時把中間節點提升到該葉子的父節點中，如果這樣使得父節點的關鍵字個數超過2M-1，則要繼續向上分裂，直到根節點，根節點的分裂會使得樹加高一層。

        為了解決上面問題，我們需要不斷地回溯，這顯然比較複雜，我們可以未雨綢繆：我們不是等到發現是否真的需要分裂一個滿節點時才做插入操作。相反地，當沿著樹向下查詢要插入關鍵字所處位置時，就分裂沿途遇到的每個滿節點。這樣做後，每當要分裂一個滿節點時，就能保證其雙親不是滿節點。

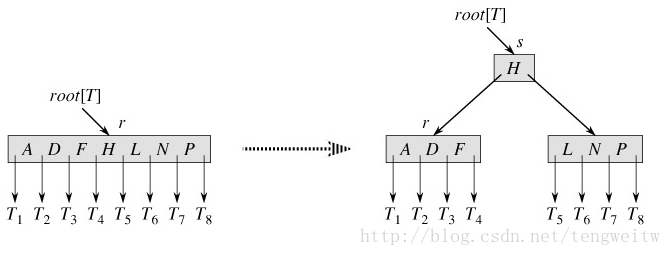
分裂滿節點的過程圖解如下：


        我們還要考慮特殊情況：當分裂一個滿的根時，需要先讓根成為一個新的空根節點的孩子，這樣才能被上面的分解過程分解。樹的高度增加1，分裂是樹增高的唯一途徑！其操作如下圖：


綜上所述，插入過程的具體實現如下：

//////////////////////////////插入部分///////////////////////////////////////////
/**********************************************************\
函式功能：節點分裂，防止違反B樹的性質
輸入： 父節點father ,子節點child，k表示子節點為父節點的哪個孩子
輸出：無
\**********************************************************/
void BtreeSplitChild(BtreeNode *father,BtreeNode *child,int k)
{
	BtreeNode *newchild=(BtreeNode *)malloc(sizeof(BtreeNode));
	newchild->isleaf=child->isleaf;//newchild為child的右節點，即child分裂為child和newchild
	newchild->num=M-1;
	for(int i=0;i<M-1;i++)
		newchild->key[i]=child->key[i+M];
	if(!child->isleaf)//當child不是葉子時，還要把指標賦給newchild
	{
		for(int j=0;j<M;j++)
			newchild->p[j]=child->p[j+M];
	}

	child->num=M-1;//child的個數由2M-1變為M-1

	for(int i=father->num-1;i>=k+1;i--)//改變父節點的內容
		father->p[i+1]=father->p[i];
	father->p[k+1]=newchild;
	for(int j=father->num-1;j>=k;j--)
		father->key[j+1]=father->key[j];
	father->key[k]=child->key[M-1];//將child的中間節點提升到父節點
	father->num=father->num+1;


}

/**********************************************************\
函式功能：x節點不是滿的情況下，插入keyword
輸入：B樹的根，要插入的關鍵字
輸出：無
\**********************************************************/
void BtreeInsertNotFull(BtreeNode *x,int keyword)
{
	int i=x->num;
	if(x->isleaf)//當x為葉子時，keyword插入到該節點中
	{
		while(i>=1&&keyword<x->key[i-1])
		{
			x->key[i]=x->key[i-1];
			i=i-1;
		}	
		x->key[i]=keyword;
		x->num=x->num+1;
	}
	else//當x不是葉子時，找到keyword要插入的節點並插入
	{
		while(i>=1&&keyword<x->key[i-1])
		{
			i=i-1;
		}
	
		if(x->p[i]->num==2*M-1)//當節點為滿節點時，需要分裂
		{
			BtreeSplitChild(x,x->p[i],i);
			if(keyword>x->key[i])
				i=i+1;
			
		}
		BtreeInsertNotFull(x->p[i],keyword);
	}
}

/**********************************************************\
函式功能：插入關鍵值
輸入：B樹的根，關鍵字
輸出：B樹的根
\**********************************************************/
BtreeNode * BtreeInsert(BtreeNode *TestNode,int keyword)
{
	if(TestNode->num==2*M-1)//當根節點為滿時，唯一增加高度的情況
	{
		BtreeNode *newroot=(BtreeNode *)malloc(sizeof(BtreeNode));
		newroot->isleaf=false;//產生新的根
		newroot->num=0;
		newroot->p[0]=TestNode;
		BtreeSplitChild(newroot,TestNode,0);
		BtreeInsertNotFull(newroot,keyword);
		return newroot;
	}
	else
	{
		BtreeInsertNotFull(TestNode,keyword);
		return TestNode;
	}

}

4.刪除

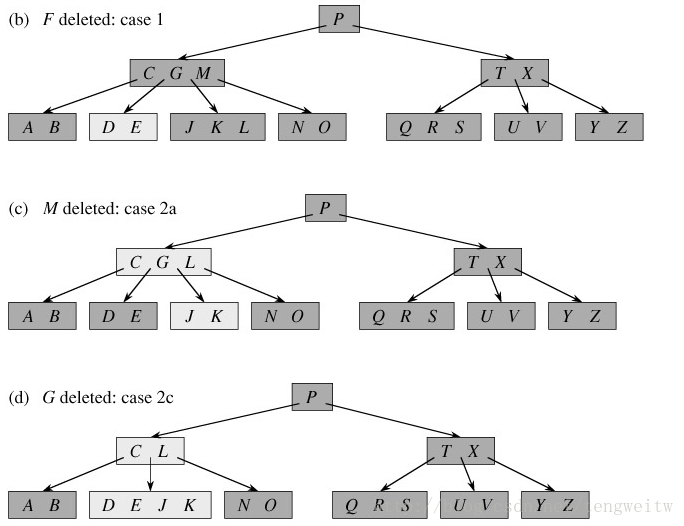
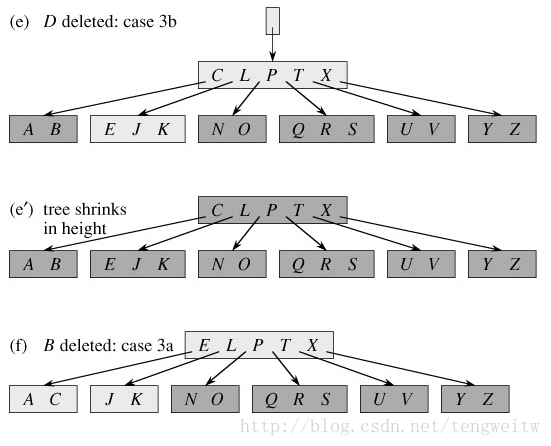
               B樹的刪除比插入操作更加複雜，插入操作只需考慮三種情況，而刪除操作需要考慮的情況很多，情況如下：


        和插入操作類似，根據B樹的規則，每個節點的關鍵字個數在[M-1, 2M-1]之間，故當keyword(要插入的關鍵字)要從某個葉子刪除時，如果該葉子節點只有有M-1個關鍵字，則再刪除keyword就違反了B樹的定義，這時就需要對該葉子節點進行合併。上圖中各種情況中的t就是我所說的M即最小度數。具體程式實現如下：

///////////////////////////刪除部分//////////////////////////////////////////
/**********************************************************\
函式功能：合併左右子節點
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeMergeChild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    // 將z中節點拷貝到y的後半部分
    y->num = 2 * M - 1;
    for(int i = M; i < 2 * M - 1; i++) 
	{
        y->key[i] = z->key[i-M];
    }
    y->key[M-1] = root->key[pos]; // 將root->key[pos]下降為y的中間節點
    
    
    if(false == z->isleaf)// 如果z是內節點即非葉子，需要拷貝指向子節點的指標p
	{
        for(int i = M; i < 2 * M; i++) 
		{
            y->p[i] = z->p[i-M];
        }
    }
     
      
    for(int j = pos + 1; j < root->num; j++) // root->key[pos]下降到y中，更新root中key和p
	{
        root->key[j-1] = root->key[j];
        root->p[j] = root->p[j+1];
    }

    root->num -= 1;
    free(z);
}
  
/**********************************************************\
函式功能：刪除關鍵字keyword
輸入：樹的根，關鍵字
輸出：樹的根
\**********************************************************/
BtreeNode *BtreeDelete(BtreeNode *root, int keyword)
{
    
    // 唯一能降低樹高的情形
    if(1 == root->num) // 當根只有一個關鍵字，兩個子女
	{
        BtreeNode *y = root->p[0];
        BtreeNode *z = root->p[1];
        if(NULL != y && NULL != z &&M - 1 == y->num && M - 1 == z->num)//兩個子女的關鍵字個數都為M-1時，合併根與兩個子女
		{
            BtreeMergeChild(root, 0, y, z);
            free(root);//注意釋放空間
            BtreeDeleteNotFull(y, keyword);
            return y;
        }
		else 
		{
            BtreeDeleteNotFull(root, keyword);
            return root;
        }
    } 
	else 
	{
        BtreeDeleteNotFull(root, keyword);    
        return root;
    }
}

/**********************************************************\
函式功能： root至少有個M個關鍵字時刪除關鍵字
輸入：   樹的根，關鍵字
輸出：   無
\**********************************************************/
void BtreeDeleteNotFull(BtreeNode *root, int keyword)
{
    if(true == root->isleaf) // 如果在葉子節點，直接刪除,情況1
	{ 
        int i = 0;
        while(i < root->num && keyword > root->key[i]) i++;
        if(keyword == root->key[i])
		{
            for(int j = i + 1; j < 2 * M - 1; j++) 
			{
                root->key[j-1] = root->key[j];
            }
            root->num -= 1;
        } 
		else 
		{
            printf("keyword not found\n");
        }
    }
	else 
	{  // 在分支中
        int i = 0;
        BtreeNode *y = NULL, *z = NULL;
        while(i < root->num && keyword > root->key[i]) i++; 
        if(i < root->num && keyword == root->key[i]) 
		{ // 如果在分支節點找到keyword
            y = root->p[i];
            z = root->p[i+1];
            if(y->num > M - 1) 
			{  
		      // 如果左分支關鍵字多於M-1，則找到左分支的最右節點pre，替換keyword
                // 並在左分支中遞迴刪除prev,情況2a
                int pre = BtreeSearchPrevious(y);
                root->key[i] = pre;
                BtreeDeleteNotFull(y, pre);//遞迴處理
            } 
			else if(z->num > M - 1)
			{
                // 如果右分支關鍵字多於M-1，則找到右分支的最左節點next，替換keyword
                // 並在右分支中遞迴刪除next,情況2b
                int next = BtreeSearchNext(z);
                root->key[i] = next;
                BtreeDeleteNotFull(z, next);
            }
			else // 兩個分支節點數都為M-1，則合併至y，並在y中遞迴刪除keyword,情況2c
			{
                
                BtreeMergeChild(root, i, y, z);
                BtreeDelete(y, keyword);
            }
        }
		else// 分支中沒有，在分支的子節點中的情況
		{   
            y = root->p[i];
            if(i < root->num) 
			{
                z = root->p[i+1];//y的右兄弟
            }
            BtreeNode *p = NULL;//初始化
            if(i > 0)
			{
                p = root->p[i-1];//y的左兄弟
            }

            if(y->num == M - 1)
			{
                if(i > 0 && p->num > M - 1) 
				{
                    // 左兄弟節點關鍵字個數大於M-1,情況3a
                    BtreeChangeToRchild(root, i-1, p, y); 
                } 
				else if(i < root->num && z->num > M - 1) 
				{
                    // 右兄弟節點關鍵字個數大於M-1,情況3a
                    BtreeChangeToLchild(root, i, y, z); 
                }
				else if(i > 0) 
				{   
                    BtreeMergeChild(root, i-1, p, y);  //左右兄弟節點都不大於M-1，情況3b
                    y = p;
                } 
				else //沒有左兄弟的情況
				{
                    BtreeMergeChild(root, i, y, z); 
                }
                BtreeDeleteNotFull(y, keyword);
            }
			else 
			{
                BtreeDeleteNotFull(y, keyword);
            }
        }

    }
}

/**********************************************************\
函式功能：尋找以root為根的最大關鍵字
輸入：    樹的根
輸出：    最大關鍵字
\**********************************************************/ 
int BtreeSearchPrevious(BtreeNode *root)
{
    BtreeNode *y = root;
    while(false == y->isleaf)
	{
        y = y->p[y->num];
    }
    return y->key[y->num-1];
}

/**********************************************************\
函式功能：尋找以root為根的最小關鍵字
輸入：樹的根
輸出：最小關鍵字
\**********************************************************/
int BtreeSearchNext(BtreeNode *root)  
{
    BtreeNode *z = root;
    while(false == z->isleaf)
	{
        z = z->p[0];
    }
    return z->key[0];
}


/**********************************************************\
函式功能：z向y借節點，將root->key[pos]下降至z，將y的最大關鍵字上升至root的pos處
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeChangeToRchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    z->num += 1;
    for(int i = z->num -1; i > 0; i--) 
	{
        z->key[i] = z->key[i-1];
    }
    z->key[0]= root->key[pos];
    root->key[pos] = y->key[y->num-1];

    if(false == z->isleaf)
	{
        for(int i = z->num; i > 0; i--) 
		{
            z->p[i] = z->p[i-1];
        }
        z->p[0] = y->p[y->num];
    }

    y->num -= 1; 
}

 
/**********************************************************\
函式功能：y向借節點，將root->key[pos]下降至y，將z的最小關鍵字上升至root的pos處
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeChangeToLchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    y->num += 1;
    y->key[y->num-1] = root->key[pos];
    root->key[pos] = z->key[0];

    for(int j = 1; j < z->num; j++)
	{
        z->key[j-1] = z->key[j];
    }

    if(false == z->isleaf) 
	{
        y->p[y->num] = z->p[0];
        for(int j = 1; j <= z->num; j++) 
		{
            z->p[j-1] = z->p[j];
        }
    } 

    z->num -= 1;
}

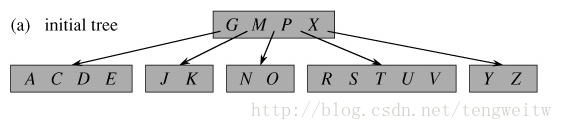
下面用具體例項來形象地說明B樹的操作：

假設初始的B樹如下：


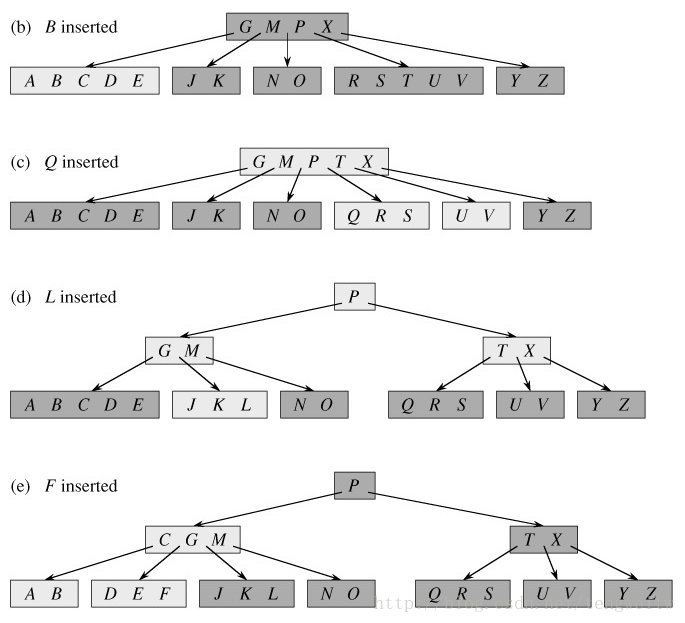
經過一系列的插入操作後：



在程式中為表示方便，將關鍵字由字母換成了數字，A、B、C……Y、Z對應於1、2、3……25、26.

經過上面的插入操作後，緊接在進行一系列刪除操作：




具體的完整例項程式實現如下：

#include<stdio.h>
#include<stdlib.h>

#define M 3

//節點結構體
typedef struct BtreeNode
{
	int num;
	struct BtreeNode *p[2*M];
	int key[2*M-1];
	bool isleaf; 
}BtreeNode;

BtreeNode * BtreeCreate();
void BtreeSplitChild(BtreeNode *father,BtreeNode *child,int k);
void BtreeInsertNotFull(BtreeNode *x,int keyword);
BtreeNode * BtreeInsert(BtreeNode *TestNode,int keyword);
BtreeNode *BtreeSearch(BtreeNode *TestNode,int keyword);

//////
void BtreeMergeChild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z);
BtreeNode *BtreeDelete(BtreeNode *root, int keyword);
void BtreeDeleteNotFull(BtreeNode *root, int keyword);
int BtreeSearchPrevious(BtreeNode *root);
int BtreeSearchNext(BtreeNode *root);
void BtreeChangeToRchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z);
void BtreeChangeToLchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z);

/**********************************************************\
函式功能：建立節點
輸入：無
輸出：新節點
\**********************************************************/
BtreeNode * BtreeCreate()
{
	BtreeNode *node=(BtreeNode *)malloc(sizeof(BtreeNode));
	if(NULL==node)
		return NULL;
	node->isleaf=true;
	node->num=0;
	for(int i=0;i<2*M;i++)
		node->p[i]=NULL;
	for(int i=0;i<2*M-1;i++)
		node->key[i]=0;
	return node;
}
//////////////////////////////插入部分///////////////////////////////////////////
/**********************************************************\
函式功能：節點分裂，防止違反B樹的性質
輸入： 父節點father ,子節點child，k表示子節點為父節點的哪個孩子
輸出：無
\**********************************************************/
void BtreeSplitChild(BtreeNode *father,BtreeNode *child,int k)
{
	BtreeNode *newchild=(BtreeNode *)malloc(sizeof(BtreeNode));
	newchild->isleaf=child->isleaf;//newchild為child的右節點，即child分裂為child和newchild
	newchild->num=M-1;
	for(int i=0;i<M-1;i++)
		newchild->key[i]=child->key[i+M];
	if(!child->isleaf)//當child不是葉子時，還要把指標賦給newchild
	{
		for(int j=0;j<M;j++)
			newchild->p[j]=child->p[j+M];
	}

	child->num=M-1;//child的個數由2M-1變為M-1
	
	for(int i=father->num;i>=k+1;i--)//改變父節點的內容
	{
		father->p[i+1]=father->p[i];
	}
	father->p[k+1]=newchild;
	for(int j=father->num-1;j>=k;j--)
		father->key[j+1]=father->key[j];
	father->key[k]=child->key[M-1];//將child的中間節點提升到父節點
	father->num=father->num+1;


}

/**********************************************************\
函式功能：x節點不是滿的情況下，插入keyword
輸入：B樹的根，要插入的關鍵字
輸出：無
\**********************************************************/
void BtreeInsertNotFull(BtreeNode *x,int keyword)
{
	int i=x->num;
	if(x->isleaf)//當x為葉子時，keyword插入到該節點中
	{
		while(i>=1&&keyword<x->key[i-1])
		{
			x->key[i]=x->key[i-1];
			i=i-1;
		}	
		x->key[i]=keyword;
		x->num=x->num+1;
	}
	else//當x不是葉子時，找到keyword要插入的節點並插入
	{
		i=x->num;
		while(i>=1&&keyword<x->key[i-1])
		{
			i=i-1;
		}
	
		if(x->p[i]->num==2*M-1)//當節點為滿節點時，需要分裂
		{
			BtreeSplitChild(x,x->p[i],i);
			if(keyword>x->key[i])
				i=i+1;
			
		}
		BtreeInsertNotFull(x->p[i],keyword);
	}
}

/**********************************************************\
函式功能：插入關鍵值
輸入：B樹的根，關鍵字
輸出：B樹的根
\**********************************************************/
BtreeNode * BtreeInsert(BtreeNode *TestNode,int keyword)
{
	if(TestNode->num==2*M-1)//當根節點為滿時，唯一增加高度的情況
	{
		
		BtreeNode *newroot=(BtreeNode *)malloc(sizeof(BtreeNode));
		newroot->isleaf=false;//產生新的根
		newroot->num=0;
		newroot->p[0]=TestNode;
		BtreeSplitChild(newroot,TestNode,0);
		BtreeInsertNotFull(newroot,keyword);
		return newroot;
	}
	else
	{
		
		BtreeInsertNotFull(TestNode,keyword);
		return TestNode;
	}

}

/**********************************************************\
函式功能：查詢關鍵字所在的節點
輸入：    樹的根，關鍵字
輸出：    關鍵字所在的節點
\**********************************************************/
BtreeNode *BtreeSearch(BtreeNode *TestNode,int keyword)
{
	int i=0;
	while(i<TestNode->num&&keyword>TestNode->key[i])
		i=i+1;
	if(i<=TestNode->num&&keyword==TestNode->key[i])
		return TestNode;
	if(TestNode->isleaf)
	{
		printf("Not founded!\n");
		return NULL;
	}
	else
	{
		return BtreeSearch(TestNode->p[i],keyword);
	}
}




///////////////////////////刪除部分//////////////////////////////////////////
/**********************************************************\
函式功能：合併左右子節點
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeMergeChild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    // 將z中節點拷貝到y的後半部分
    y->num = 2 * M - 1;
    for(int i = M; i < 2 * M - 1; i++) 
	{
        y->key[i] = z->key[i-M];
    }
    y->key[M-1] = root->key[pos]; // 將root->key[pos]下降為y的中間節點
    
    
    if(false == z->isleaf)// 如果z是內節點即非葉子，需要拷貝指向子節點的指標p
	{
        for(int i = M; i < 2 * M; i++) 
		{
            y->p[i] = z->p[i-M];
        }
    }
     
      
    for(int j = pos + 1; j < root->num; j++) // root->key[pos]下降到y中，更新root中key和p
	{
        root->key[j-1] = root->key[j];
        root->p[j] = root->p[j+1];
    }

    root->num -= 1;
    free(z);
}
  
/**********************************************************\
函式功能：刪除關鍵字keyword
輸入：樹的根，關鍵字
輸出：樹的根
\**********************************************************/
BtreeNode *BtreeDelete(BtreeNode *root, int keyword)
{
    
    // 唯一能降低樹高的情形
    if(1 == root->num) // 當根只有一個關鍵字，兩個子女
	{
        BtreeNode *y = root->p[0];
        BtreeNode *z = root->p[1];
        if(NULL != y && NULL != z &&M - 1 == y->num && M - 1 == z->num)//兩個子女的關鍵字個數都為M-1時，合併根與兩個子女
		{
            BtreeMergeChild(root, 0, y, z);
            free(root);//注意釋放空間
            BtreeDeleteNotFull(y, keyword);
            return y;
        }
		else 
		{
            BtreeDeleteNotFull(root, keyword);
            return root;
        }
    } 
	else 
	{
        BtreeDeleteNotFull(root, keyword);    
        return root;
    }
}

/**********************************************************\
函式功能： root至少有個M個關鍵字時刪除關鍵字
輸入：   樹的根，關鍵字
輸出：   無
\**********************************************************/
void BtreeDeleteNotFull(BtreeNode *root, int keyword)
{
    if(true == root->isleaf) // 如果在葉子節點，直接刪除,情況1
	{ 
        int i = 0;
        while(i < root->num && keyword > root->key[i]) i++;
        if(keyword == root->key[i])
		{
            for(int j = i + 1; j < 2 * M - 1; j++) 
			{
                root->key[j-1] = root->key[j];
            }
            root->num -= 1;
        } 
		else 
		{
            printf("keyword not found\n");
        }
    }
	else 
	{  // 在分支中
        int i = 0;
        BtreeNode *y = NULL, *z = NULL;
        while(i < root->num && keyword > root->key[i]) i++; 
        if(i < root->num && keyword == root->key[i]) 
		{ // 如果在分支節點找到keyword
            y = root->p[i];
            z = root->p[i+1];
            if(y->num > M - 1) 
			{  
		      // 如果左分支關鍵字多於M-1，則找到左分支的最右節點pre，替換keyword
                // 並在左分支中遞迴刪除prev,情況2a
                int pre = BtreeSearchPrevious(y);
                root->key[i] = pre;
                BtreeDeleteNotFull(y, pre);//遞迴處理
            } 
			else if(z->num > M - 1)
			{
                // 如果右分支關鍵字多於M-1，則找到右分支的最左節點next，替換keyword
                // 並在右分支中遞迴刪除next,情況2b
                int next = BtreeSearchNext(z);
                root->key[i] = next;
                BtreeDeleteNotFull(z, next);
            }
			else // 兩個分支節點數都為M-1，則合併至y，並在y中遞迴刪除keyword,情況2c
			{
                
                BtreeMergeChild(root, i, y, z);
                BtreeDelete(y, keyword);
            }
        }
		else// 分支中沒有，在分支的子節點中的情況
		{   
            y = root->p[i];
            if(i < root->num) 
			{
                z = root->p[i+1];//y的右兄弟
            }
            BtreeNode *p = NULL;//初始化
            if(i > 0)
			{
                p = root->p[i-1];//y的左兄弟
            }

            if(y->num == M - 1)
			{
                if(i > 0 && p->num > M - 1) 
				{
                    // 左兄弟節點關鍵字個數大於M-1,情況3a
                    BtreeChangeToRchild(root, i-1, p, y); 
                } 
				else if(i < root->num && z->num > M - 1) 
				{
                    // 右兄弟節點關鍵字個數大於M-1,情況3a
                    BtreeChangeToLchild(root, i, y, z); 
                }
				else if(i > 0) 
				{   
                    BtreeMergeChild(root, i-1, p, y);  //左右兄弟節點都不大於M-1，情況3b
                    y = p;
                } 
				else //沒有左兄弟的情況
				{
                    BtreeMergeChild(root, i, y, z); 
                }
                BtreeDeleteNotFull(y, keyword);
            }
			else 
			{
                BtreeDeleteNotFull(y, keyword);
            }
        }

    }
}

/**********************************************************\
函式功能：尋找以root為根的最大關鍵字
輸入：    樹的根
輸出：    最大關鍵字
\**********************************************************/ 
int BtreeSearchPrevious(BtreeNode *root)
{
    BtreeNode *y = root;
    while(false == y->isleaf)
	{
        y = y->p[y->num];
    }
    return y->key[y->num-1];
}

/**********************************************************\
函式功能：尋找以root為根的最小關鍵字
輸入：樹的根
輸出：最小關鍵字
\**********************************************************/
int BtreeSearchNext(BtreeNode *root)  
{
    BtreeNode *z = root;
    while(false == z->isleaf)
	{
        z = z->p[0];
    }
    return z->key[0];
}


/**********************************************************\
函式功能：z向y借節點，將root->key[pos]下降至z，將y的最大關鍵字上升至root的pos處
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeChangeToRchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    z->num += 1;
    for(int i = z->num -1; i > 0; i--) 
	{
        z->key[i] = z->key[i-1];
    }
    z->key[0]= root->key[pos];
    root->key[pos] = y->key[y->num-1];

    if(false == z->isleaf)
	{
        for(int i = z->num; i > 0; i--) 
		{
            z->p[i] = z->p[i-1];
        }
        z->p[0] = y->p[y->num];
    }

    y->num -= 1; 
}

 
/**********************************************************\
函式功能：y向借節點，將root->key[pos]下降至y，將z的最小關鍵字上升至root的pos處
輸入：根，左右子節點，左節點是父節點的第pos個節點
輸出：無
\**********************************************************/
void BtreeChangeToLchild(BtreeNode *root, int pos, BtreeNode *y, BtreeNode *z)
{
    y->num += 1;
    y->key[y->num-1] = root->key[pos];
    root->key[pos] = z->key[0];

    for(int j = 1; j < z->num; j++)
	{
        z->key[j-1] = z->key[j];
    }

    if(false == z->isleaf) 
	{
        y->p[y->num] = z->p[0];
        for(int j = 1; j <= z->num; j++) 
		{
            z->p[j-1] = z->p[j];
        }
    } 

    z->num -= 1;
}


//按層次遍歷B樹
void Print(BtreeNode *root)
{	
	int front,rear;
	int num=0;
	int num1=0;
	int flag=0;
	BtreeNode *queue[100];
	BtreeNode *s;
	if(root!=NULL)
	{
		rear=1;
		front=0;
		queue[rear]=root;
		while(front<rear)
		{
			front++;
		
			s=queue[front];

			if(!s->isleaf)
			{
				for(int j=0;j<=s->num;j++)
				{
					if(s->p[j]!=NULL)
					{
						rear++;
						queue[rear]=s->p[j];
						
					}
				}
			}
			
		}
			for(int k=1;k<=rear;k++)//使輸出簡單易看
			{	
				for(int i=0;i<queue[k]->num;i++)
					printf("%d ",queue[k]->key[i]);
				printf("| ");			
				if(k>num)
				{
					
					while(flag<k)
					{
					num=num+queue[flag+1]->num+1;
					flag++;
					}
				printf("\n");
				flag=k;
				}
				
			}
			
			
		
	}
}


////////////////////////////////////////////////////////////////////////////
void main()
{
/**************************初始化**************************/
	BtreeNode *TestNode=BtreeCreate();
	BtreeNode *Node1=BtreeCreate();
	BtreeNode *Node2=BtreeCreate();
	BtreeNode *Node3=BtreeCreate();
	BtreeNode *Node4=BtreeCreate();
	BtreeNode *Node5=BtreeCreate();
	BtreeNode *root=BtreeCreate();

	BtreeNode *SearchNode=BtreeCreate();
	TestNode->isleaf=false;
	TestNode->num=4;
	TestNode->key[0]=7;
	TestNode->key[1]=13;
	TestNode->key[2]=16;
	TestNode->key[3]=24;
	TestNode->p[0]=Node1;
	TestNode->p[1]=Node2;
	TestNode->p[2]=Node3;
	TestNode->p[3]=Node4;
	TestNode->p[4]=Node5;

	Node1->isleaf=true;
	Node1->num=4;
	Node1->key[0]=1;
	Node1->key[1]=3;
	Node1->key[2]=4;
	Node1->key[3]=5;

	Node2->isleaf=true;
	Node2->num=2;
	Node2->key[0]=10;
	Node2->key[1]=11;


	Node3->isleaf=true;
	Node3->num=2;
	Node3->key[0]=14;
	Node3->key[1]=15;


	Node4->isleaf=true;
	Node4->num=5;
	Node4->key[0]=18;
	Node4->key[1]=19;
	Node4->key[2]=20;
	Node4->key[3]=21;
	Node4->key[4]=22;


	Node5->isleaf=true;
	Node5->num=2;
	Node5->key[0]=25;
	Node5->key[1]=26;
	root=TestNode;
/*******************************初始化結束***********************/
	printf("原始B樹：\n");
	Print(root);
	root=BtreeInsert(root,2);
	printf("\n插入關鍵字為2後的B樹：\n");
	Print(root);
	root=BtreeInsert(root,17);
	printf("\n插入關鍵字為17後的B樹：\n");
	Print(root);
	root=BtreeInsert(root,12);
	printf("\n插入關鍵字為12後的B樹：\n");
	Print(root);
	root=BtreeInsert(root,6);
	printf("\n插入關鍵字為6後的B樹：\n");
	Print(root);
	printf("\n\n");
	//刪除操作
    root=BtreeDelete(root,6);
	printf("\n刪除關鍵字為6後的B樹：\n");
	Print(root);

	root=BtreeDelete(root,13);
	printf("\n刪除關鍵字為13後的B樹：\n");
	Print(root);

	root=BtreeDelete(root,7);
	printf("\n刪除關鍵字為7後的B樹：\n");
	Print(root);

	root=BtreeDelete(root,4);
	printf("\n刪除關鍵字為4後的B樹：\n");
	Print(root);


    root=BtreeDelete(root,2);
	printf("\n刪除關鍵字為2後的B樹：\n");
	Print(root);
	
}

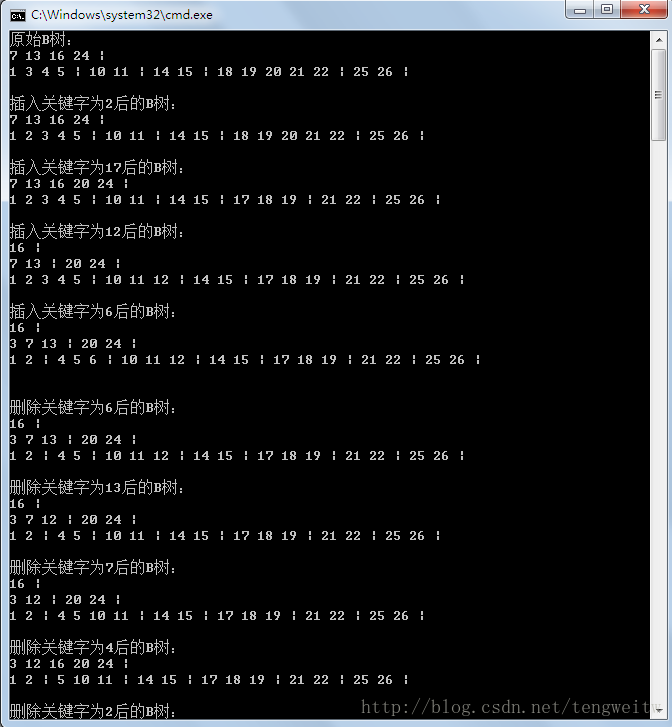
程式結果如下（| 用於分開不同節點的關鍵字，下圖顯示是按樹的層次遍歷的，可以看出結果與上面插入和刪除的圖解過程完全相同！）：


注：如果程式出錯，可能是使用的開發平臺版本不同，請點選如下連結： 解釋說明

作者：nineheadedbird


相關推薦

【演算法導論】B樹

      一棵B樹T是具有如下性質的有根樹（設根為root）: 1.每個節點x有一下域：   （a）num,當前儲存在節點x的關鍵字個數,關鍵字以非降序存放，因此key[i]<=key[i+1]<=……key[n]；   （b）isleaf,是一個bool值

【演算法總結】B+樹的實現

【參考資料】 【B+樹是什麼】 b+樹是b樹的變種。b+樹與b樹最大的不同在於：b+樹的關鍵字數量跟孩子節點數量一致，這與b樹不一樣。並且，b+樹的葉子節點包含有所有關鍵字及其對應資訊，非葉子節點只包含部分關鍵字（這部分關鍵字相當於邊界索引），不含具體資料，下面這幅圖就

【演算法總結】B樹總結

【參考資料】 【B樹解釋】 B樹是一棵樹，不同的是該樹的最多有m個子節點，至少floor（m/2）個子節點（根節點除外，根節點最少可以有兩個子節點。），但是裡面包含關鍵字數量比當前的子節點少1，在沒有子節點的情況下，關鍵字數量在 floor（m/2）-1到m-1之間。

【演算法導論】求二叉樹的葉子數和深度

/**********************************************\ 函式功能：計算葉子節點個數 輸入： 二叉樹的根節點 輸出： 葉子節點個數 \**********************************************/ int countleaf(

二叉排序樹（Binary Sort Tree，二叉查詢樹，二叉搜尋樹）--【演算法導論】

今天的收穫就是二叉搜尋樹，“好記性不如爛筆頭”，寫下來加深一下印象； 1、首先是瞭解了二叉搜尋樹（Binary Sort Tree）又稱二叉查詢樹，亦稱二叉排序樹。 若它的左子樹不空，則左子樹上所有結點的值均小於它的根結點的值； 若它的右子樹不空，則右子樹上所有結點的值均

【演算法導論】二叉排序樹

具體程式實現如下： /**************************************\ 函式功能：在二叉排序樹中刪除節點 輸入： 二叉排序樹的根節點、要刪除的節點的內容 輸出： 二叉排序樹的根節點 \*************************************

【演算法導論】 第十課 平衡搜尋樹

         樹的結構，如果不能保持平衡，那麼其搜尋效能會大大打折扣，而本節課介紹了幾種經典的平衡樹，如AVL，2-3-4tree，紅黑樹等等，然後著重講了紅黑樹，接下來就紅黑樹的基本性質，作一些簡短的總結。    首先，紅黑樹除了具有BST的基本性質外，還額外擁有以下

演算法導論 之 B樹 B-樹 - 建立 插入 C語言

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

演算法導論 之 B樹 - 刪除 C語言

分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

【演算法導論】歸併排序

#include <iostream> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cstring> #include <string&g

【演算法導論】3.1~3.2

2018年10月31日 19:42:50 mahaoyuan2015 閱讀數：4 個人分類： 讀書筆記

【演算法導論】7

快速排序 程式碼： #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> int partition(int a[], int p, int r) {

演算法導論 之 B樹 B-樹

                作者：鄒祁峰郵箱：[email protected]日期：2014.03.13 18:00轉載請註明來自"祁峰"的CSDN部落格1 引言  In computer science, a B-tree is a tree data structure that keep

【資料結構】B樹、B+樹與B*樹詳解

B樹 1.B樹的定義 B樹（B-tree）是對2-3樹資料結構的擴充套件，又稱為多路平衡查詢樹，它的一個節點可以擁有多於2個子節點的二叉查詢樹。與自平衡二叉查詢樹不同， B樹是一種自平衡樹資料結構，可以保持資料排序，它能夠儲存資料、對其進行排序並允許以

演算法導論 之 B樹(B-樹)

作者：鄒祁峰 郵箱：[email protected] 日期：2014.03.13 18:00 轉載請註明來自"祁峰"的CSDN部落格 1 引言   In computer science, a B-tree is a tree data structure

【資料結構】B樹和B+樹講解

一、B樹 1、B樹的定義     B樹是一種平衡的多分樹，通常我們說m階的B樹，它必須滿足如下條件：     （1）每個結點至多有m個子結點；     （2）除根結點和葉結點外，其它每個結點至少有個子結點；     （3）若根結點不是葉子結點，則至少有兩個子結點；   

【原理思路】B+樹原理

B+樹，是B-樹的變形，是為檔案系統需要而設計的一種平衡查詢樹； B+樹定義： 每一個結點含有如下內容或滿足的規則： （1）指標域：存放指向資料的指標，也可以與關鍵字存放在一起； （2）key_number：當前儲存在結點x中的關鍵字數; （3）key[key_numbe

【資料結構】B樹/B+樹

本篇博文旨在介紹一種適合外查詢的樹---B樹，以及B樹的延伸B+樹；比較了B樹和B+樹的各自優缺點；說明了B樹B+樹的應用場景；以及實現了B樹的程式碼 B樹 B樹的概念和性質 B樹是一種適合外查詢的樹，它是一種多叉平衡樹 除此之外，它還滿足如下的性質： （1）根節點有至少

演算法導論 之 B-樹(B樹)

1 引言 In computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, a

【演算法導論】動態規劃切鋼條

問題：鋼條切割    給定長度為n英寸的鋼條，和一個價格表P{1....n}，求切割鋼條的方案，使得收益R最大。如果鋼條價格足夠大，可以完全不用切割。 來源：演算法導論，第15章 方法：1、遞迴窮舉；2、動態規劃 思路： 遞迴窮舉：鋼條分為兩部分左邊為不切割部分範圍長度j