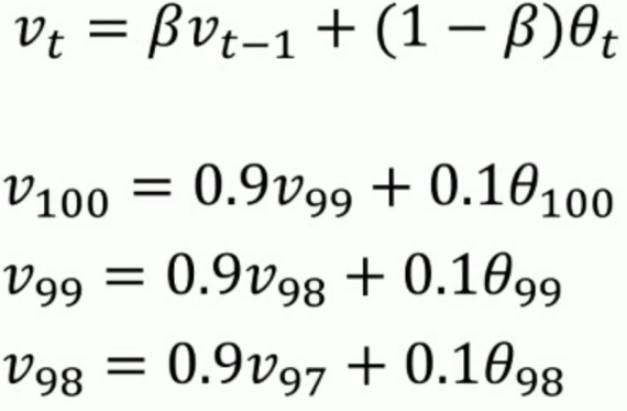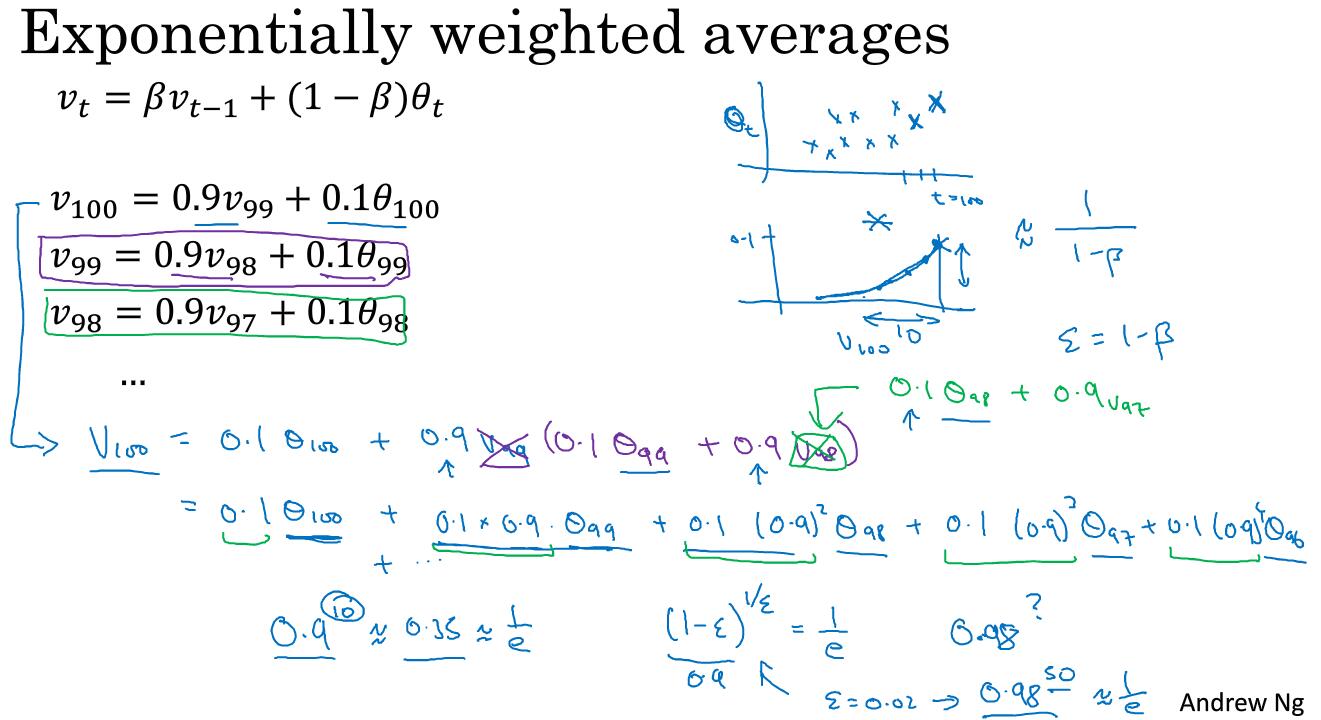2.2.2 指數加權平均
阿新 • • 發佈:2019-02-19
指數加權平均
下面介紹一下比梯度下降更快的演算法,不過在這之前,你要了解指數加全平均。
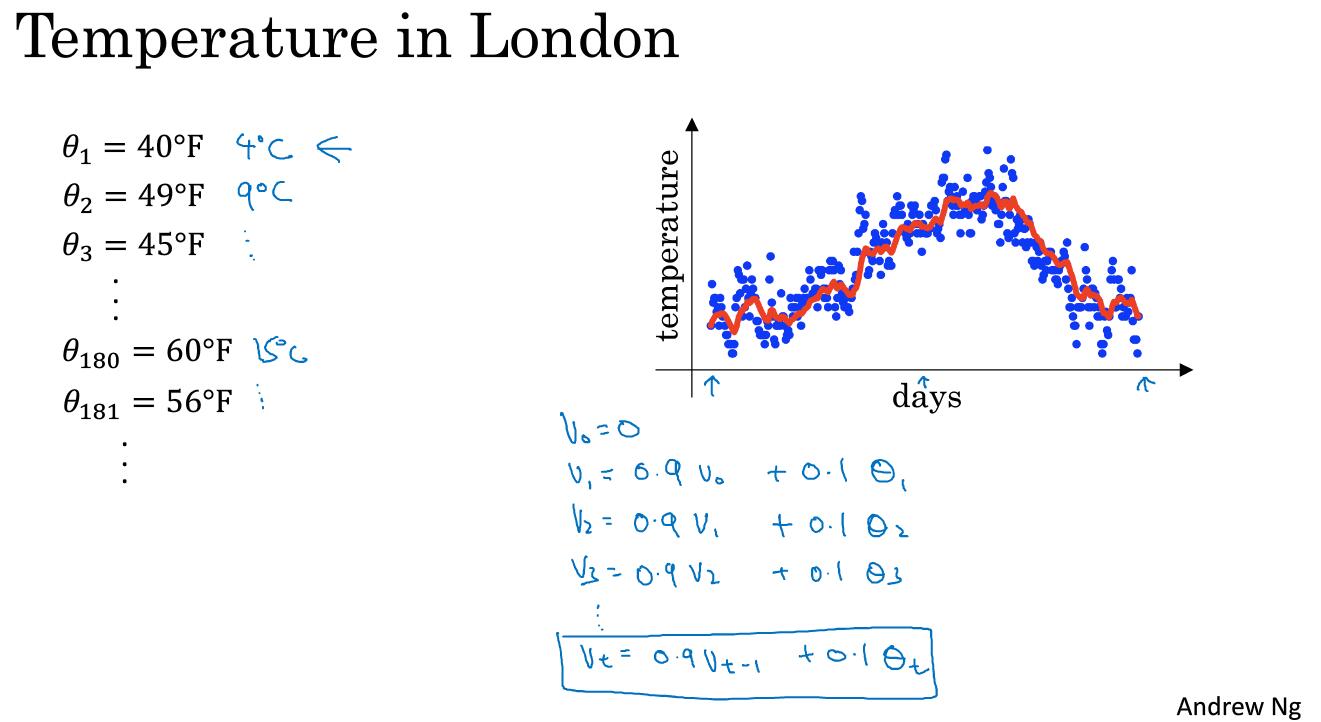
如1和2所示,指數加權實際上就是設定一個權值。就像下圖所示
通過
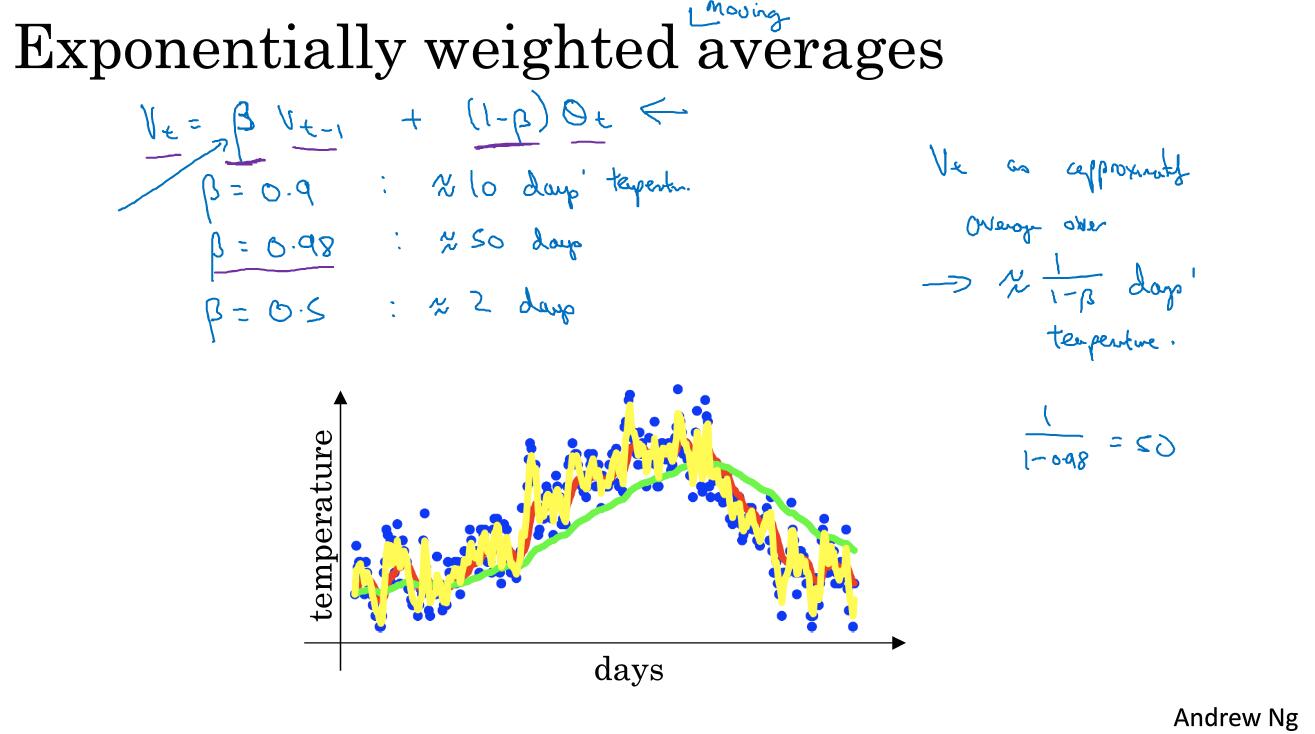
來計算是平均的多少天。
理解指數加權平均
如下圖所示
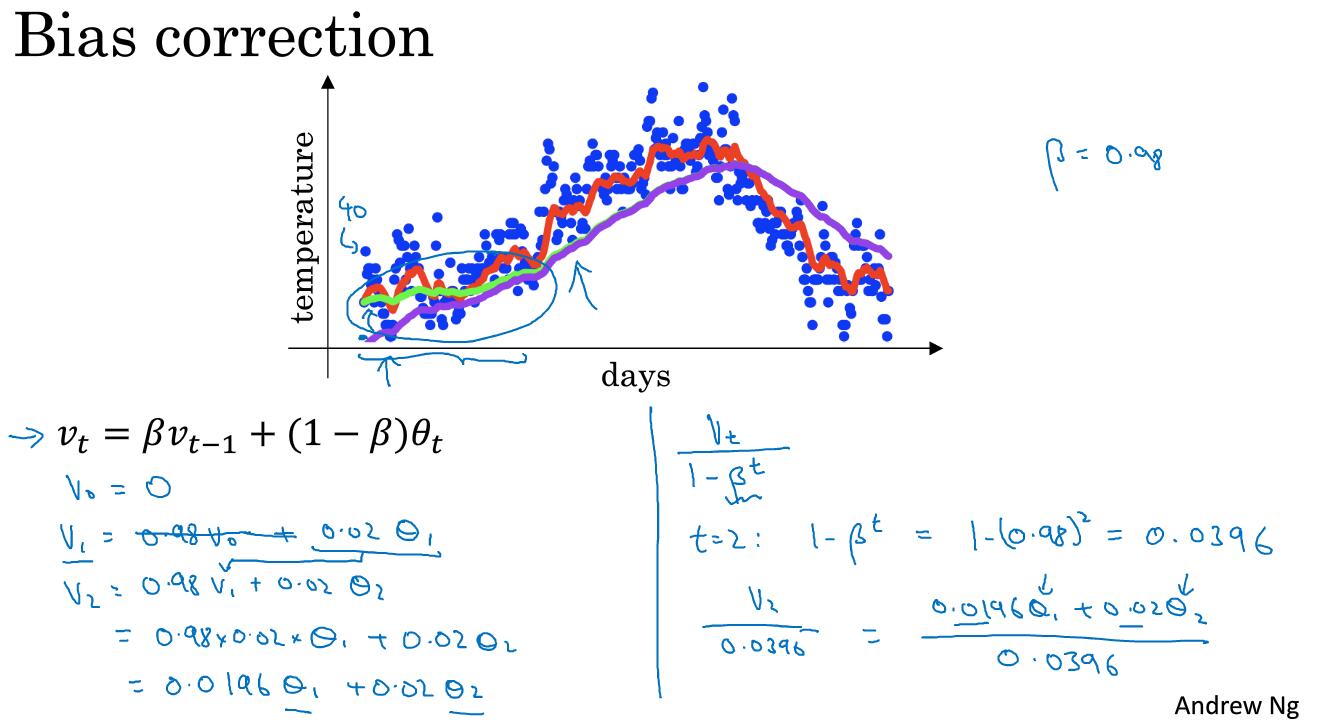
我們要算第100天的平均溫度可以寫成圖中下面0.9的指數形式。由上圖是每天的實際溫度,下面是0.1通過指數衰減過後的函式值。對於v_100而言,這些所有的係數相加和近似為1,我們稱這個為偏差修正。
那麼一般情況下我們到底平均多少天的氣溫就可以了呢?
可以看到0.9的10次方差不多等於1/e,此時權重差不多下降到整體權重的三分之一,我們有公式
這個n值差不多就是我們想要的了。
最後我們來講一下實際如何執行。
演算法如上圖所示的右側。這實際上是一個遞迴的過程。如右下圖所示,就是一個不斷更新
的過程。
指數加權平均的偏差修正
偏差修正可以讓指數加權平均算的更為準確一些,下面介紹一下是如何做的。
如圖左側所示,按照我們指數加權平均公式,等於0,所以的預測值會比的實際值要低上不少。因為所佔的比重也很低,計算出來的預測值比實際值底。那麼有沒有什麼好的解決辦法呢?讓估值初期的值與實際值更接近一些。
方法就是如圖右側所示,我們更新公式,給分母加一個權重
我們可以發現,隨著t的不斷增加,分母會越來越接近於1,這樣就保證了加權平均並且除去了偏差。當t不斷增加的時候,修正偏差幾乎沒有作用。