There are well-known formulas: 

,   , . 

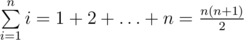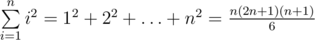Also mathematicians found similar formulas for higher degrees.

Find the value of the sum  modulo 109 + 7 (so you should find the remainder after dividing the answer by the value 109 + 7).

The only line contains two integers n

Print the only integer a — the remainder after dividing the value of the sum by the value 109 + 7.

4 1

10

4 2

30

4 3

100

4 0

4

題意：求自然數冪和： modulo 109 + 7

程式碼：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;

const ll mod = 1e9+7;
const int maxn = 1e6+5;
ll f[maxn], fac[maxn];
ll pow(ll a, ll b) {                         //快速冪取模
    ll ret = 1; 
    while(b) {
        if(b&1)
            ret = (ret*a)%mod;
        a = (a*a)%mod;
        b>>=1;
    }
    return ret;
}

int main()
{
    ll n, k;
    cin>>n>>k;
    for(int i = 1; i<=k+2; i++) {            //求自然數冪和的前k+2項； 
        f[i] = (f[i-1]+pow(i*1LL, k))%mod;
    }

    if(n<=k+2) {
        cout<<f[n]<<endl;
        return 0;
    }

    fac[0] = 1;                              //求前k+2項階乘；
    for(int i = 1; i<=k+2; i++) {
        fac[i] = (fac[i-1]*i)%mod;
    }


    ll cur = 1, ans = 0;                     //預處理分式的分子；
    for(int i = 1; i<=k+2; i++) {
        cur = (cur*(n-i))%mod;
    }

    for(int i = 1; i<=k+2; i++) {
        ll inv1 = pow(n-i, mod-2)%mod;                               //對(n-i)求逆元；
        ll inv2 = pow(fac[i-1]%mod*fac[k+2-i]%mod, mod-2)%mod;       //對階乘求逆元；
        int sign = (k+2-i)%2?-1:1;                                   //判正負；
        ans = (ans + sign*inv1*inv2%mod*f[i]%mod*cur%mod)%mod;
    }
    ans = (ans+mod)%mod;
    cout<<ans<<endl;
    return 0;
}