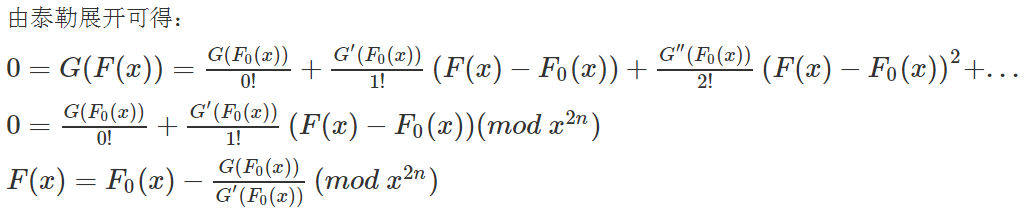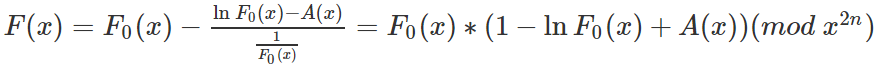題意:連結

方法:多項式求冪+拉格朗日反演。

解析:

毒瘤題最後一個。

首先先寫幾個公式(勿問證明)

Fk(x)=exp(k∗ln(F(X)))

若F(G(x))=G(F(x))=x

則稱F(x)與G(x)互為複合逆

若F(x)為G(x)的複合逆

[xn]F(x)表示F(x)的n次方項系數

則有[xn]F(x)=1n[xn−1](xG(x))n

推廣

[xn]H(F(x))=1n[xn−1]H′(x)(xG(x))n

然而這題用不到推廣，別怕- -!

我們顯然可以搞出來d的生成函式。

我們設F(x)是根節點點權的生成函式。

則

F(x)=∑i∈DFi(x)+x

+x代表他是葉節點時。

再搞出來D中元素的生成函式C(x)

則

F(x)=C(F(x))+x

設G(x)=x−C(x)

則有

G(F(x))=x

所以F(x)是G(x)的複合逆。

於是有

[xn]F(x)=1n[xn−1](xG(x))n

如果細心一點發現，(xG(x))上下可以同約一個x,這樣的話可以保證這個東西是可求ln的，因為常數項就變成1了，所以我們不必進行一些關於常數項的轉化什麼的。

出題人良心！

求exp怎麼求呢？

無腦倍增….

上圖是牛頓迭代。

然後我們帶進上圖的式子。

然後就可以無腦倍增了…

神奇！

程式碼:

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define N 262244
#define mod 950009857
using namespace std;
typedef long long ll;
int s,m,l;

int rev[N];

ll G[N],G_inv[N],G_inv_n[N],G_inv_dao[N],G_inv_ln[N];
ll inv[N];
void init()
{
    inv[1
 
]=1;
    for(int i=2;i<l;i++)
        inv[i]=(mod-mod/i)*inv[mod%i]%mod;
}
ll Quick_Power(ll x,ll y,ll MOD)
{
    ll ret=1;
    while(y)
    {
        if(y&1)ret=(ret*x)%MOD;
        x=(x*x)%MOD;
        y>>=1;
    }
    return ret;
}

void NTT(ll *a,int n,int f)
{
    for(int i=0;i<n;i++)if(i<rev[i])swap(a[i],a[rev[i]]);
    for(int h=2;h<=n;h<<=1)
    {
        ll wn=Quick_Power(7,(mod-1)/h,mod);
        for(int i=0;i<n;i+=h)
        {
            ll w=1;
            for(int j=0;j<(h>>1);j++,w=w*wn%mod)
            {
                ll t=a[i+j+(h>>1)]*w%mod;
                a[i+j+(h>>1)]=((a[i+j]-t)%mod+mod)%mod;
                a[i+j]=(a[i+j]+t)%mod;
            }
        }
    }
    if(f==-1)
    {
        for(int i=1;i<(n>>1);i++)swap(a[i],a[n-i]);
        ll inv=Quick_Power(n,mod-2,mod);
        for(int i=0;i<n;i++)a[i]=(long long)a[i]*inv%mod;
    }
}
void Get_Inv(ll *a,ll *b,int n)
{
    static ll temp[N];
    if(n==1)
    {
        b[0]=Quick_Power(a[0],mod-2,mod);
        return;
    }
    Get_Inv(a,b,n>>1);
    memcpy(temp,a,sizeof(a[0])*n);
    memset(temp+n,0,sizeof(a[0])*n); 
    int m=n,L=0,nn=n;
    for(n=1;n<=m;n<<=1)L++;
    for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(temp,n,1),NTT(b,n,1);
    for(int i=0;i<n;i++)
        temp[i]=b[i]*(((2ll-temp[i]*b[i]%mod)%mod+mod)%mod)%mod;
    NTT(temp,n,-1);
    for(int i=0;i<(n>>1);i++)b[i]=temp[i];
    memset(b+nn,0,sizeof(b[0])*nn);
    n=nn;
}
void Get_Ln(ll *a,ll *b,int n)
{
    static ll a_dao[N],a_inv[N];
    for(int i=1;i<=n;i++)
        a_dao[i-1]=a[i]*i%mod;
    a_dao[n]=0;
    Get_Inv(a,a_inv,n);
    int m=n,L=0;
    for(n=1;n<=m;n<<=1)L++;
    for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(a_inv,n,1),NTT(a_dao,n,1);
    for(int i=0;i<n;i++)
        b[i]=a_inv[i]*a_dao[i]%mod;
    NTT(b,n,-1);
    for(int i=n-1;i>=1;i--)
        b[i]=b[i-1]*inv[i]%mod;
    b[0]=0;
    memset(b+m,0,sizeof(b[0])*m);
    memset(a_dao,0,sizeof(a_dao[0])*n);
    memset(a_inv,0,sizeof(a_inv[0])*n);
}
void Get_Exp(ll *a,ll *b,int n)
{
    static ll temp[N];
    if(n==1)
    {
        b[0]=1;
        return;
    }
    Get_Exp(a,b,n>>1);
    memset(temp,0,sizeof(a[0])*(n<<1));
    Get_Ln(b,temp,n);
    for(int i=0;i<n;i++)
        temp[i]=((i==0)+mod-temp[i]+a[i])%mod;
    int m=n,L=0,nn=n;
    for(n=1;n<=m;n<<=1)L++;
    for(int i=0;i<n;i++)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(b,n,1),NTT(temp,n,1);
    for(int i=0;i<n;i++)
        b[i]=b[i]*temp[i]%mod;
    NTT(b,n,-1);
    memset(b+nn,0,sizeof(b[0])*nn);
    n=nn;
}
int main()
{
    scanf("%d%d",&s,&m);
    G[0]=1;
    for(int i=1;i<=m;i++)
    {
        ll x;
        scanf("%lld",&x);
        G[x-1]=mod-1;
    }
    for(l=1;l<=s;l<<=1);
    init();
    Get_Inv(G,G_inv,l);
    Get_Ln(G_inv,G_inv_ln,l);
    for(int i=0;i<l;i++)
        G_inv_ln[i]=G_inv_ln[i]*s%mod;  
    Get_Exp(G_inv_ln,G_inv_n,l);
    printf("%lld\n",G_inv_n[s-1]*Quick_Power(s,mod-2,mod)%mod);
}