線性代數學習點(六):二維直角座標系下的向量表示
翻譯過程稍有刪減
在原點為O的二維直角座標系中,向量v可表示為一個起點在原點的帶箭頭的線段,其終點位於點P(a, b),如下圖所示。這時,向量v可表示為一對有序陣列[a, b],其中數字a稱為向量v的x軸分量,其中數字b稱為向量v的y軸分量。
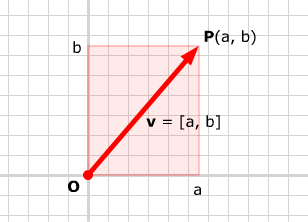
需要說明的是,當點P位於第一象限,a 和 b分別為包含向量v的矩形的寬和高,如上圖所示。如果點P位於其它象限,則a 或 b可能為負值,因此,通常稱|a| 和 |b|分別為包含向量v的矩形的寬和高.
上面所說的是用座標系中的一個點來定義一個向量,反過來,我們也可以用向量來描述座標系中的一個點。
對於x-y平面的任意一點P,總有一個起點位於原點,終點位於該點的向量與之對應。我們稱這個向量為該點的方位向量(position vector)。於是有:
- 點 P(a, b)有一個位置向量 OP,其 分量為 [a, b].
- 一個分量為 [a, b]的向量,對應了一個點P(a, b)的方位向量P(a, b).
方位向量給出了一個點相對於座標原點的偏離程度。在處理向量的幾何問題時,用方位向量可以帶來很大的方便。因為這時可以用方位向量描述直線或者平面上所有的點。
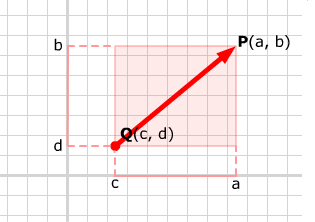
現在假定有一個向量,其起點不在原點O,而是位於點Q(c, d),如下圖所示,它的分量該如何表示呢?
無論向量的起點終點在哪裡,上述方法都適用。更嚴格一些,或者說更通用一些的表述是,若一個向量起點為Q(c,
d),終點為P(a, b),則其分量可表示為PQ=
[a - c, b - d]。
上述向量的分量描述與點的表示非常類似。這裡還有另外一種表示方法,也是使用分量,但不易引起混淆。
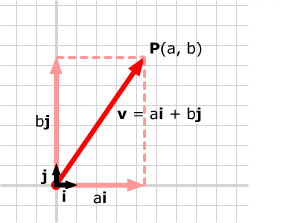
定義兩個特殊的向量 i =[1, 0]和j = [0, 1]。這兩個向量的長度均為1,其方向分別位於x軸和y軸上。這兩個特殊的向量稱為單位向量。這時,對於任意向量v