翻譯過程稍有刪減

        向量的相加通常有兩種方式：三角形法則和平行四邊形法則。

三角形法則

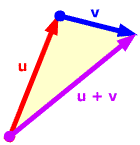
        在幾何上，要將兩個位移向量結合在一起，一個顯然的策略是第一個向量的終點即為第二個向量的起點，如下圖所示。

        這即是向量加法三角形法則或者說“起點終點”法則的基礎：將第二個向量的起點置於第一個向量的終點，這樣，和向量的起點為第一個向量的起點，和向量的終點為第二個向量的終點。

平行四邊形法則

        另外一個方面，如果有兩個力作用在同一目標上，要將這兩個力向量合成，更好的選擇是兩個向量的起點相同，如下圖所示。

        這即是向量相加平行四邊形法則或者說“起點起點”法則的基礎：將兩個向量的起點置於同一個點。兩個向量構成平行四邊形的兩條邊，平行四邊形的對角線即為和向量，如上圖所示。

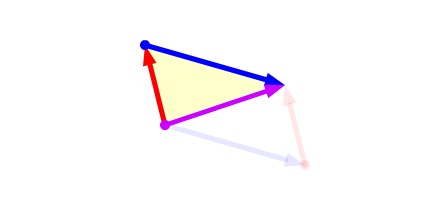
        幸運的是，這兩個法則得到的結果是相同的：平行四邊形的一半即為三角形，如下圖所示。圖中，紫色向量為紅色向量和藍色向量的和向量。

        如果相加的兩個向量中有一個為0向量，由於0向量的起點和終點重合，因此無論是根據三角形法則還是平行四邊形法則，任意向量與0向量相加的結果是該向量： u + 0 = u or 0 + v =v.

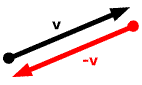
        對於任一給定向量的負向量，其長度與原向量相同，但方向完全相反，如下圖所示。

任意向量與其負向量相加的結果為0向量：v + (-v) = 0.

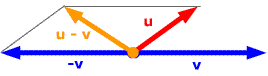
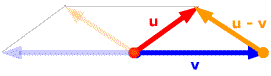
         藉助負向量，對於向量的相減，我們可以表述為一個向量與另一個向量的負向量相加： u - v = u + (-v)，如下圖所示。

         上圖是按照平行四邊形法則得到的結果，如果平移 u – v，將其起點置於 v的終點，那麼其終點則位於u的終點，如下圖所示。

        因此，如果u和 v有相同的起點，那麼從三角形法則的觀點看 u