深度學習之解讀VGGNet
為什麼提出
提出的背景
提出目的即為了探究在大規模影象識別任務中,卷積網路深度對模型精確度有何影響。
這個網路的結構用的都是特別小的3x3的卷積模版(stride:1,padding:1),以及5個2x2的池化層(stride:2),將卷積層的深度提升到了16-19層,並在當年ImageNet挑戰中再定位和分類問題上取得地第一第二的好成績。
基本思想及其過程
VGGNet網路配置情況:
為了在公平的原則下探究網路深度對模型精確度的影響,所有卷積層有相同的配置,即卷積核大小為3x3,步長為1,填充為1;共有5個最大池化層,大小都為2x2,步長為2;共有三個全連線層,前兩層都有4096通道,第三層共1000路及代表1000個標籤類別;最後一層為softmax層;所有隱藏層後都帶有ReLU非線性啟用函式;經過實驗證明,AlexNet中提出的區域性響應歸一化(LRN)對效能提升並沒有什麼幫助,而且還浪費了記憶體的計算的損耗。
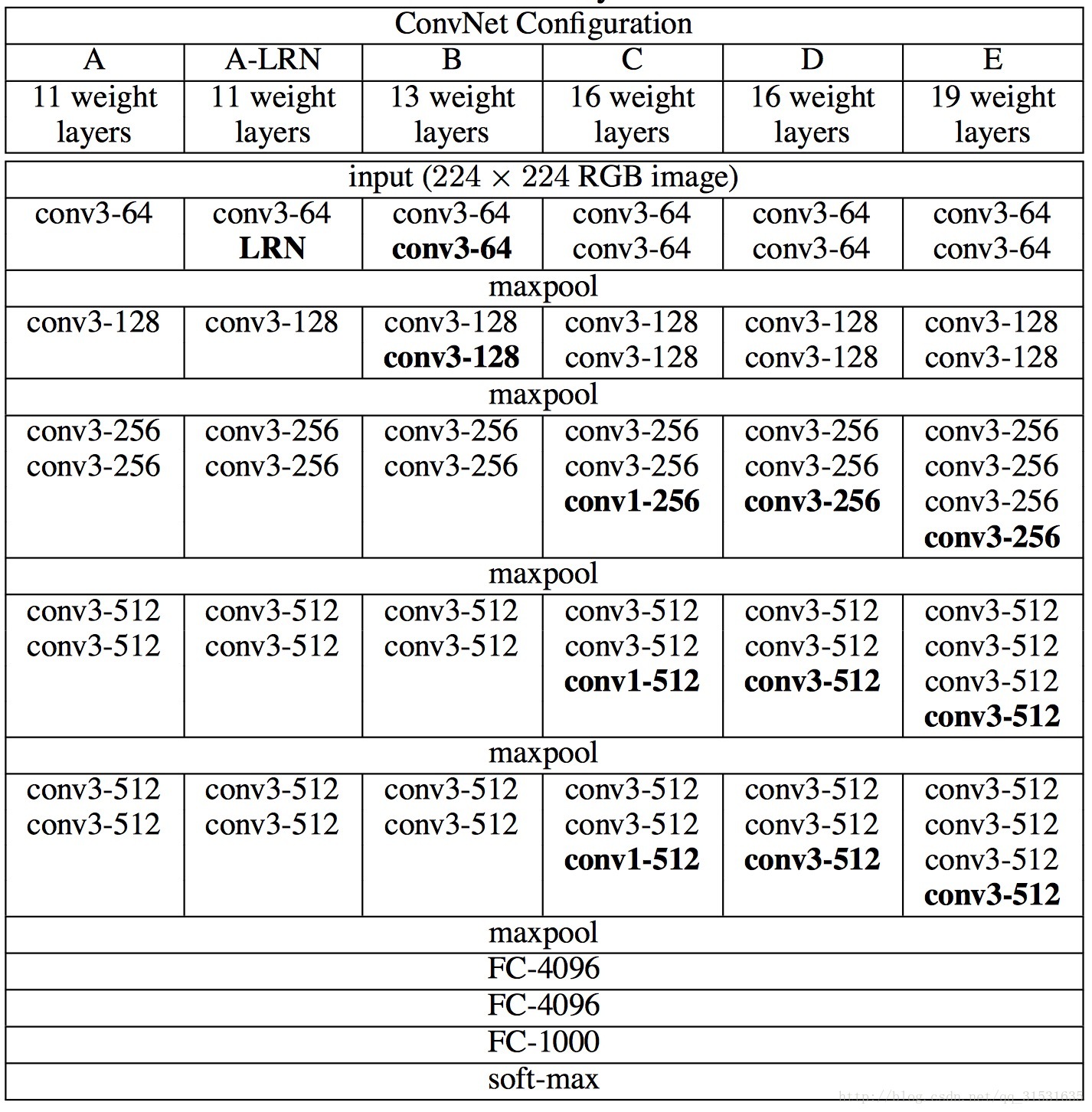

上述圖為VGGNet網路框圖,從左至右每一列代表著深度增加的不同的模型,從上至下代表模型的深度,其中conv<濾波器大小>-<通道數>,至於為什麼用3x3的濾波器尺寸,是因為這是能捕捉到各個方向的最小尺寸了,如ZFNet中所說,由於第一層中往往有大量的高頻和低頻資訊,卻沒有覆蓋到中間的頻率資訊,且步長過大,容易引起大量的混疊,因此濾波器尺寸和步長要儘量小;這裡使用1x1的卷積模版是因為1x1就相當於可以看作是一種對輸入通道進行線性變換的操作(增加決策函式的非線性且不會影響到感受野的大小)。
上面第二個圖為各個模型中用到的引數分析圖,可以看到隨著層數的增加A-E,引數增加的並不是很多,因此也分析出層數的增加可以提升效能的同時,也不會在引數量的計算儲存損耗上,有非常多的增加。
之前的網路都用7x7,11x11等比較大的卷積核,現在全用3x3不會有什麼影響嗎?
實際上,一個5x5可以用兩個3x3來近似代替,一個7x7可以用三個3x3的卷積核來代替,不僅提升了判別函式的識別能力,而且還減少了引數;如3個3x3的卷積核,通道數為C,則引數為3x(3x3xCxC)=27
而1x1卷積層的合併是一種增加決策函式的非線性的方式,而且還沒有影響到卷積層的感受野。
訓練:
訓練使用加動量的小批基於反向傳播的梯度下降法來優化多項邏輯迴歸目標。批數量為256,動量為0.9,權值衰減引數為5x
為了獲得初始化的224x224大小的圖片,通過在每張圖片在每次隨機梯度下降SGB時進行一次裁減,為了更進一步的增加訓練集,對每張圖片進行水平翻轉以及進行隨機RGB色差調整。
初始對原始圖片進行裁剪時,原始圖片的最小邊不宜過小,這樣的話,裁剪到224x224的時候,就相當於幾乎覆蓋了整個圖片,這樣對原始圖片進行不同的隨機裁剪得到的圖片就基本上沒差別,就失去了增加資料集的意義,但同時也不宜過大,這樣的話,裁剪到的圖片只含有目標的一小部分,也不是很好。
針對上述裁剪的問題,提出的兩種解決辦法:
(1) 固定最小遍的尺寸為256
(2) 隨機從[256,512]的確定範圍內進行抽樣,這樣原始圖片尺寸不一,有利於訓練,這個方法叫做尺度抖動scal jittering,有利於訓練集增強。 訓練時運用大量的裁剪圖片有利於提升識別精確率。
測試:
測試圖片的尺寸不一定要與訓練圖片的尺寸相同,且不需要裁剪。
測試的時候,首先將全連線層轉換到卷積層,第一個全連線層轉換到一個7x7的卷積層,後面兩個轉換到1x1的卷積層,這不僅讓全連線網應用到整個未裁剪的整個原始影象上,而且得到一個類別的得分圖,其通道數等於類別數,還有一個決定與輸入圖片尺寸的可變空間解析度。為了獲得固定尺寸的圖片的得分圖,運用原始圖片的softmax的後驗概率以及其水平翻轉的平均來獲得。
下圖為各個模型運用在ILSVRC-2012資料集上的結果(測試圖片尺寸固定為一個值時)。
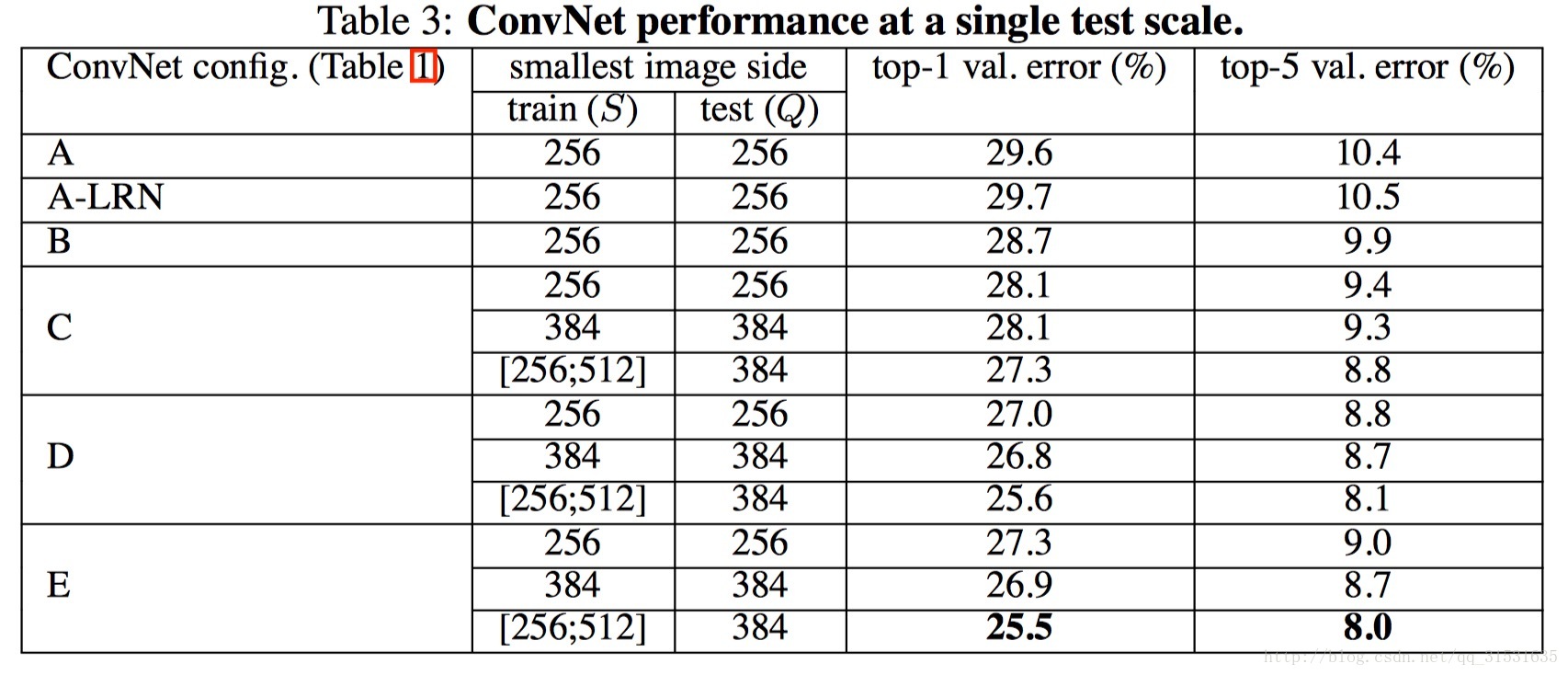
更直接地看即
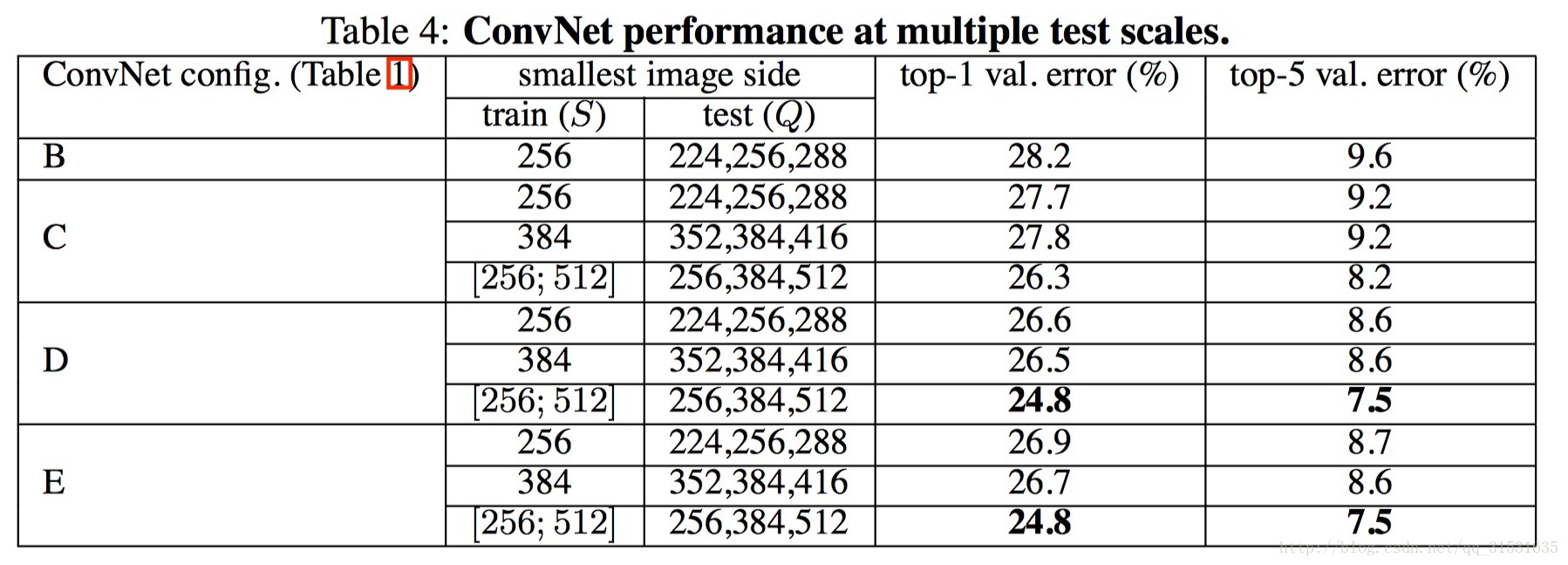
若設定測試圖片的尺寸不一,利用尺度抖動scale jittering的方法取三個值,然後取結果的平均值。
可以看到結果稍好於前者測試圖片採用單一尺寸的效果。
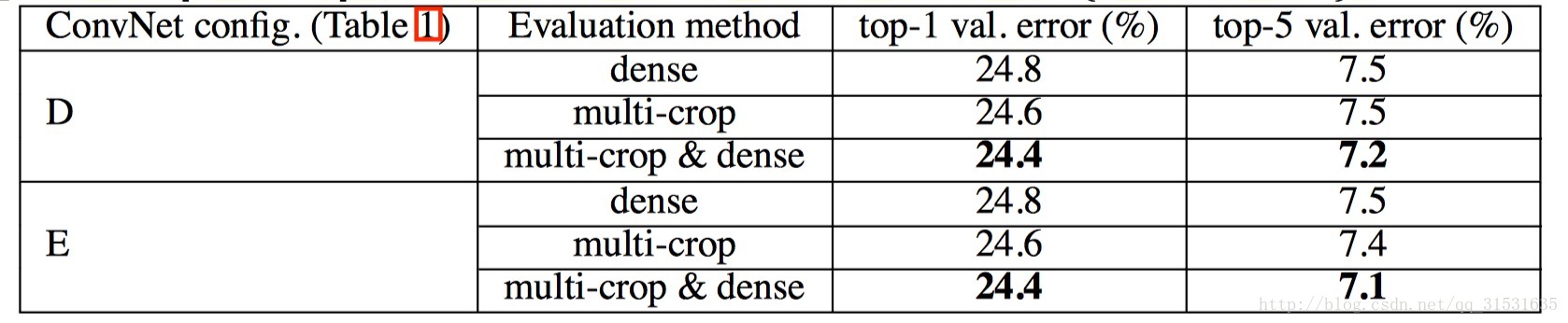
當取訓練圖片S利用尺度抖動的方法範圍為[256;512],測試圖片也利用尺度抖動取256,384,512三個值進行分類結果平均值,然後探究對測試圖片進行多裁剪估計的方法,即對三個尺度上每個尺度進行50次裁剪(5x5大小的正常網格,並進行兩次翻轉)即總共150次裁剪的效果圖,如下。
可以看到這個效果比之前兩個效果更進一步,說明多尺度裁剪也起了一定好的作用。
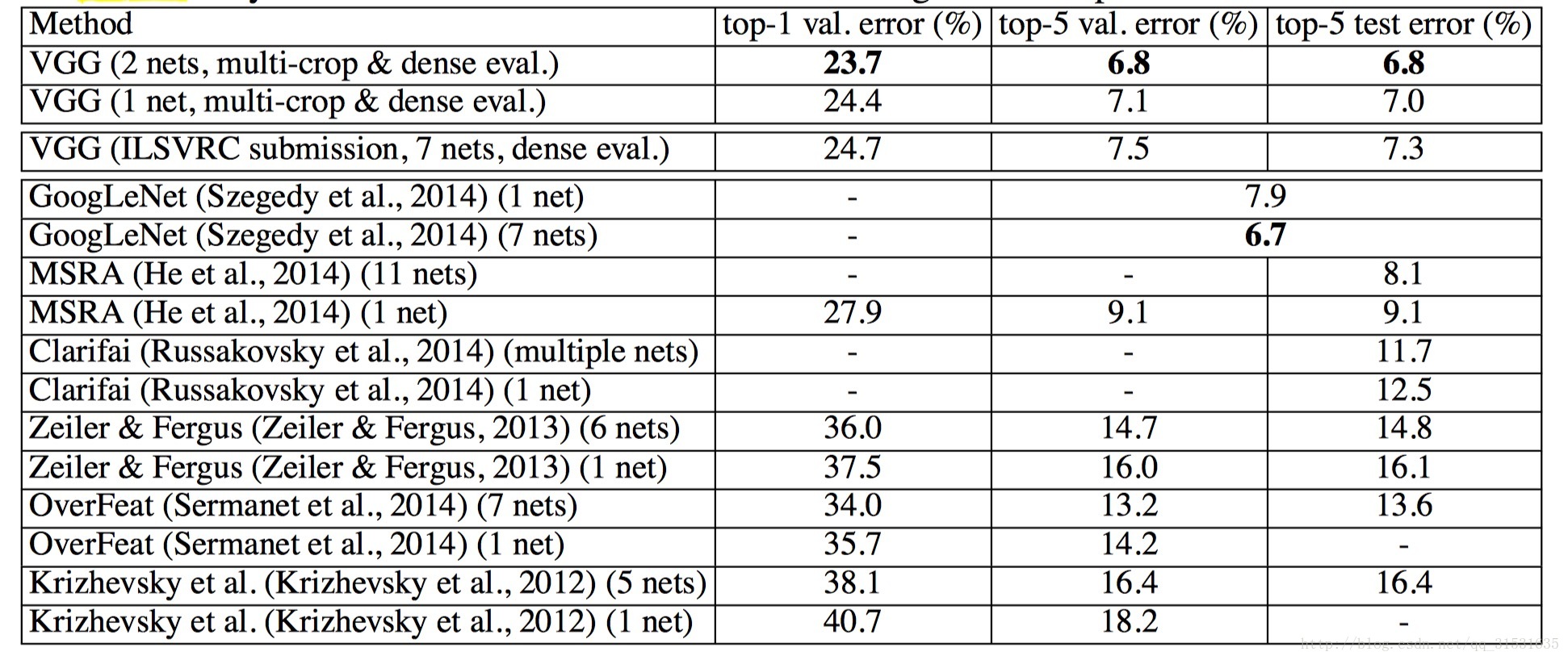
最後將多個模型進行合併進一步得到了更好的效果,並在ILSVRC比賽上拿到了第二的成績。
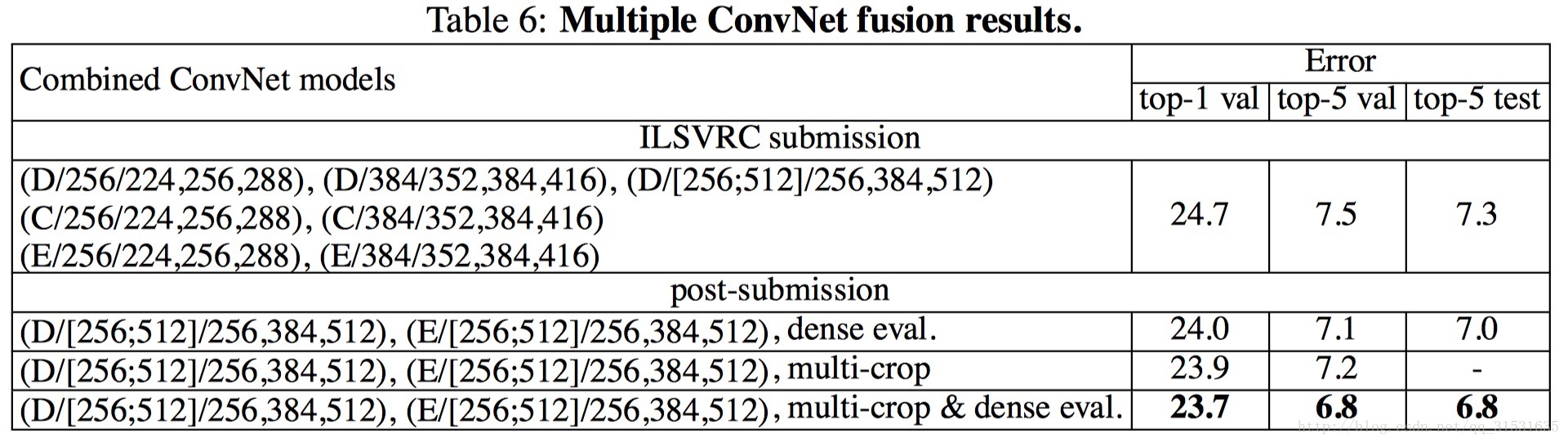

</div>](https://img-blog.csdn.net/20170504150642577?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQvcXFfMzE1MzE2MzU=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/SouthEast)