幾種計算機視覺中常用的聚類演算法(K-means, Agglomerative clustering, Mean shift, Spectral clustering)
阿新 • • 發佈:2019-02-20
對於機器學習而言,聚類常常應用於離散情況下的非監督學習演算法之中,如下圖所示。
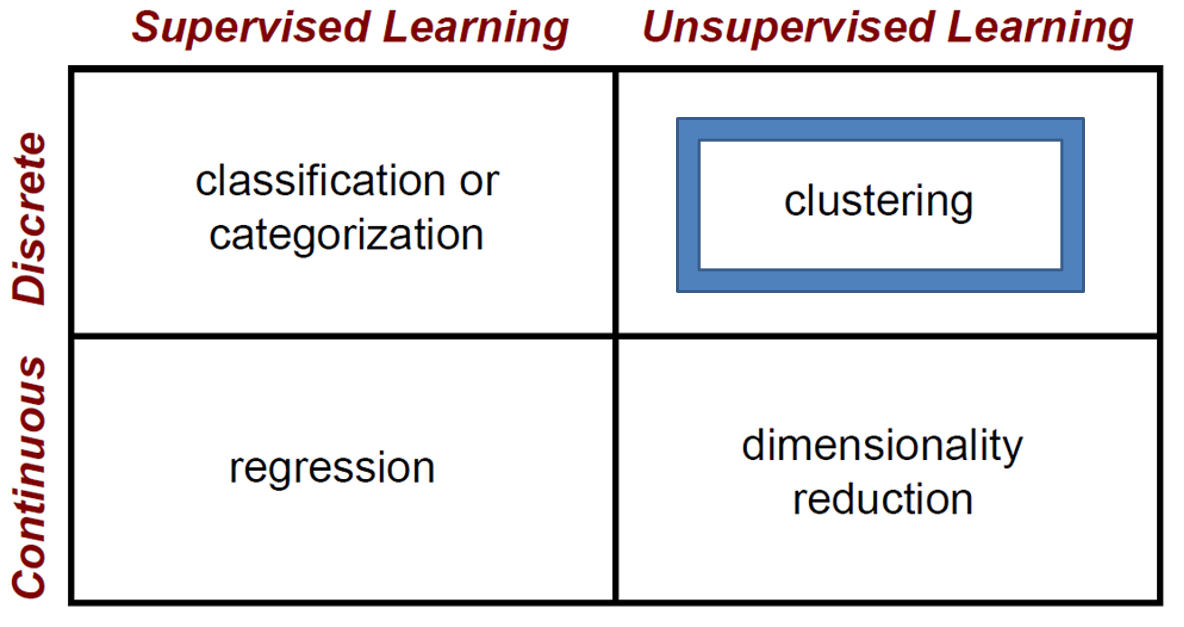
聚類的總體目標是使得最小化目標函式:
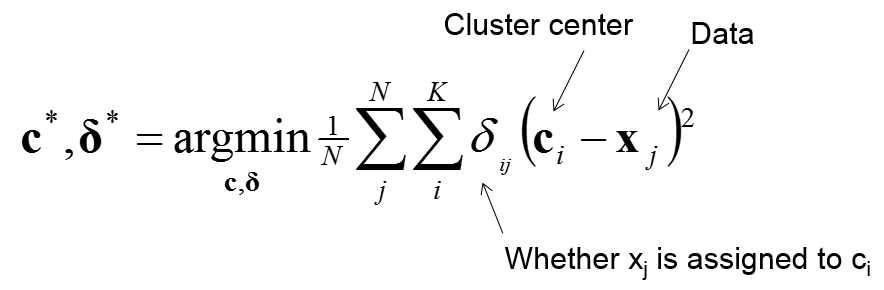
聚類的方法很多,常用的包括(K-means, Agglomerative clustering,mean shift, Spectral clustering)。
1. K-means
核心思想為迭代的指定點到最近的聚類中心。聚類演算法會收斂到區域性極小值。
演算法的有點包括:
l 簡單快速(不針對大型的聚類問題)
l 容易實現
l 能很好的表示資料
缺點包括
l 需要設定k
l 對outliers很敏感
l 收斂到區域性極小值
l 對於大型的聚類問題,其演算法複雜度較高,可能導致執行很慢
基本原理:
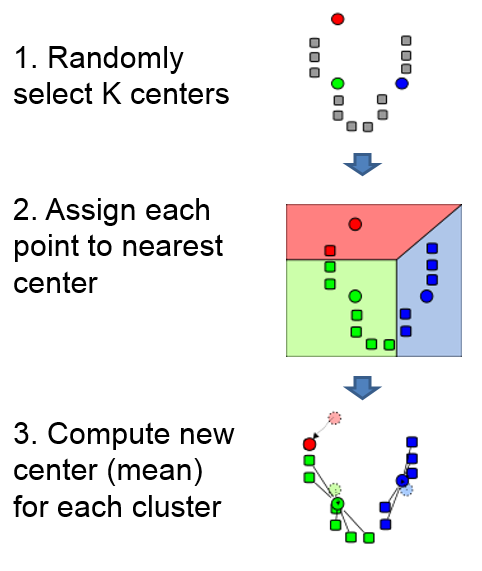
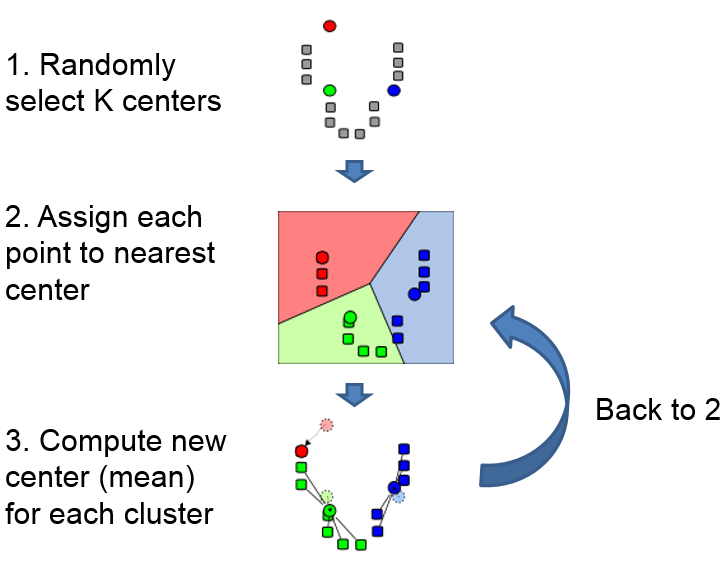
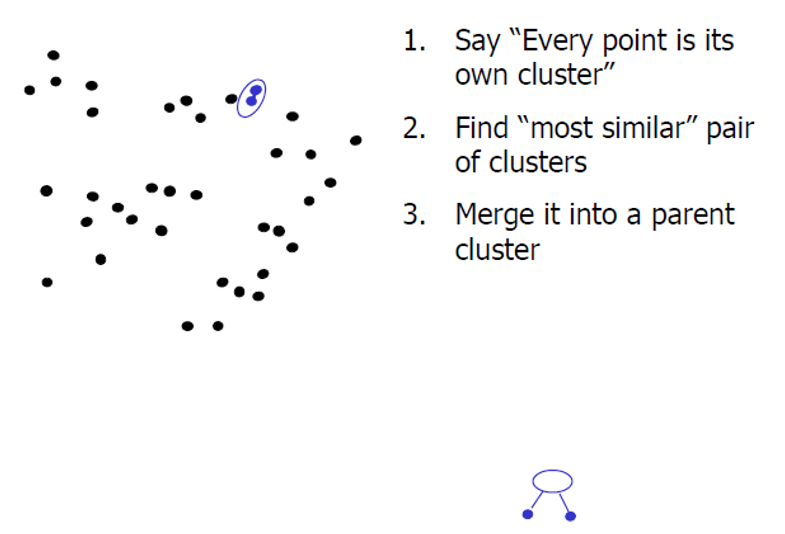
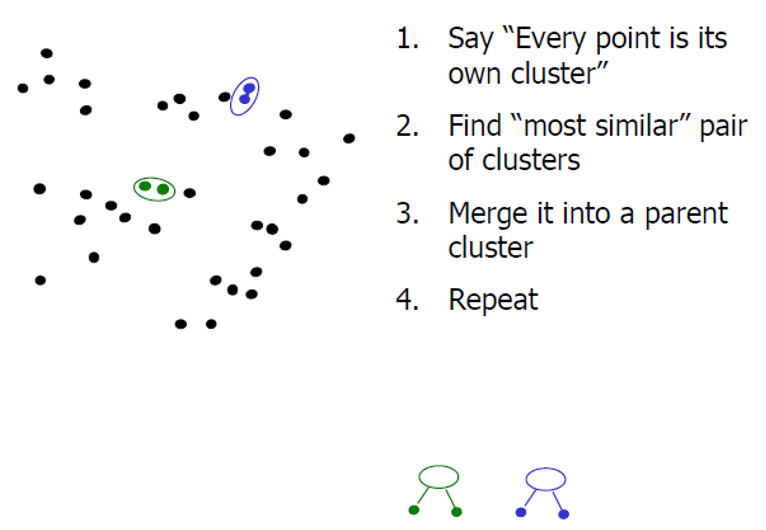
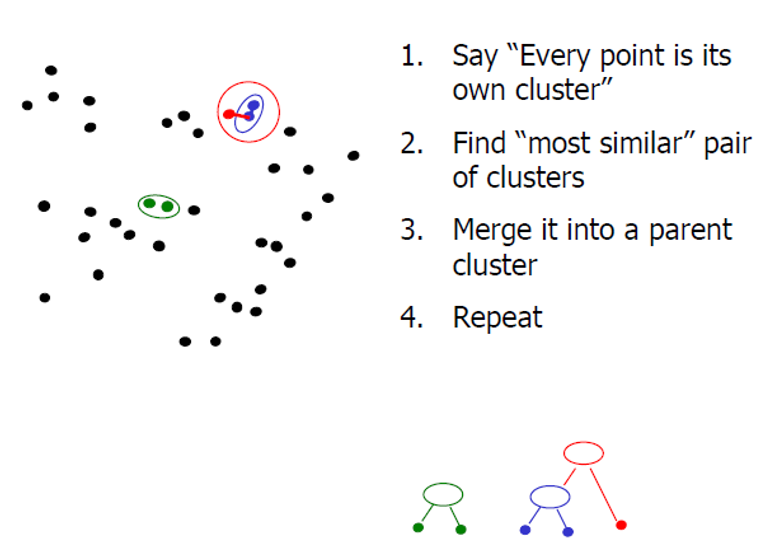
2. Agglomerative clustering
基本思想為:從每一個點開始作為一個類,然後迭代的融合最近的類。能建立一個樹形層次結構的聚類模型
演算法優點為:
l 易於實現,具有廣泛的應用
l 擁有一定的自適應形狀
l 可提供層級聚類
演算法缺點:
l 仍然需要選擇聚類的個數或者設定相關的閾值
l 可能會導致聚類不平衡(如一個類超大,一個類超小)
基本原理為:


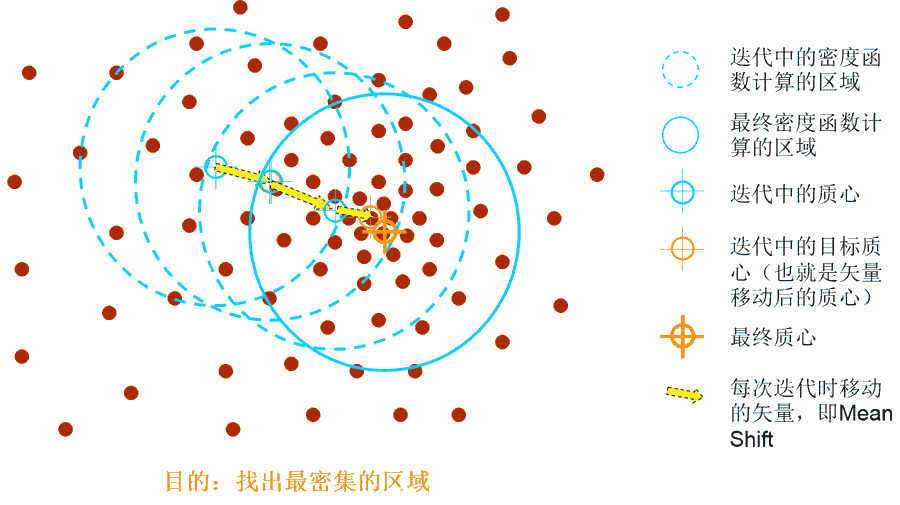
3. Mean shift
演算法優點為:
l 對outliers很魯棒
l 不需要預先設聚類的個數或者區域
演算法缺點為:
l 需要設定核的尺寸
l 不適合特徵維數很高的聚類
4. Spectral clustering

