K-中心點演算法也是一種常用的聚類演算法，K-中心點聚類的基本思想和K-Means的思想相同，實質上是對K-means演算法的優化和改進。在K-means中，異常資料對其的演算法過程會有較大的影響。在K-means演算法執行過程中，可以通過隨機的方式選擇初始質心，也只有初始時通過隨機方式產生的質心才是實際需要聚簇集合的中心點，而後面通過不斷迭代產生的新的質心很可能並不是在聚簇中的點。如果某些異常點距離質心相對較大時，很可能導致重新計算得到的質心偏離了聚簇的真實中心。

演算法步驟：

（1）確定聚類的個數K。

（2）在所有資料集合中選擇K個點作為各個聚簇的中心點。

（3）計算其餘所有點到K箇中心點的距離，並把每個點到K箇中心點最短的聚簇作為自己所屬的聚簇。

（4）在每個聚簇中按照順序依次選取點，計算該點到當前聚簇中所有點距離之和，最終距離之後最小的點，則視為新的中心點。

（5）重複（2），（3）步驟，直到各個聚簇的中心點不再改變。

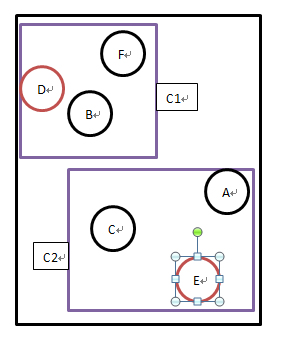
如果以樣本資料{A,B,C,D,E,F}為例，期望聚類的K值為2，則步驟如下：

（1）在樣本資料中隨機選擇B、E作為中心點。

（2）如果通過計算得到D,F到B的距離最近，A,C到E的距離最近，則B,D,F為聚簇C1，A,C,E為聚簇C2。

（3）在C1和C2兩個聚類集合中，計算一個點到其他店的距離之和的最小值作為新的中心點，假如分別計算出D到C1中其他所有點的距離之和最小，E到C2中其他所有點的距離之和最小。

（4）再以D,E作為聚簇的中心點，重複上述步驟，知道中心點不再改變。

K-中心聚類演算法計算的是某點到其它所有點的距離之後最小的點，通過距離之和最短的計算方式可以減少某些孤立資料對聚類過程的影響。從而使得最終效果更接近真實劃分，但是由於上述過程的計算量會相對杜宇K-means，大約增加O（n）的計算量，因此一般情況下K-中心演算法更加適合小規模資料運算。