光線跟蹤是目前常用的主流繪製技術之一，由於它能方便地模擬生成複雜的光照效果，生成高質量的影象，在很多領域得到了廣泛的應用，如真實感繪製，虛擬現實，視覺化，計算機動畫等。但光線跟蹤演算法的計算開銷較大，妨礙了其應用效率。光線跟蹤渲染的主要運算操作耗費在光線與場景求交的過程中，為此，為了加快這一計算過程，人們研究了大量的技術來加快求交操作。其中，通過建立一定的空間組織結構來加速求交計算機取得了很大的進展，如基於場景的空間層次劃分結構等。

對場景進行層次化的樹形結構劃分與組織，可使得空白區域能以較大的結點表示，從而減少光線穿過空白區域的開銷。目前已經被學者提出肯經常使用的空間劃分方式有均勻網格劃分、層次包圍劃分、八叉樹、KD-Tree等，這些方法在此前論文中均有所研究，且都得到了相應不錯的加速效果。而其中最為常用、且被證明效果較好的當屬KD-Tree。

1. 基於KD-Tree的場景空間劃分

為了對場景與光線相交的碰撞檢測過程進行加速，對場景的空間劃分組織不可缺少。當前主要使用的空間劃分技術有基於空間劃分的均勻網格，八叉樹，KD-Tree等，

以及結合這幾個劃分方式的混合結構。這些結構各有特點，需要根據所處理的場景的特點及繪製任務進行相應的劃分方式的選擇，沒有哪一種空間劃分方法能

最優地處理各種場景。不過這些通過空間劃分來對光線和場景之間的相交檢測進行加速的基本原理相同，即是將場景中的原始幾何體元抽象化後向上層組織，比

如以包圍盒的形式，通過首先對包圍盒進行與光線的碰撞檢測進而來排除那此不可能與光線相交的幾何體元與光線之間的相交測試。

1.1 KD-Tree的優勢

針對不同的場景可以有不同的空間劃分方式，不過當前對於光線跟蹤所使用的主流空間劃分方式為KD-Tree，這主要是因為以下幾個原因：

1. KD-Tree是一種特殊的BSP樹，它將BSP劃分中的任意分割平面退化為軸對齊的分割平面，這樣就降低了BSP生成時的幾何體元分割操作。但是它卻同樣具有BSP樹

的優良特徵，即一定程度上的啟發式空間劃分，這樣可以使得到的最終劃分二叉樹儘可能地平衡，這樣就降低了最壞情況下的光線與劃分結構之間的求交次數，進而提升的效率。

2. 由於KD-Tree是一種二叉樹，因此在遍歷的時間就要比八叉樹等非二叉樹的劃分結構更簡單，這也推廣了它的使用範圍。

3. 最後，很重要的一點是由於二叉樹遍歷的簡易性可以使它們比較容易移植於不支援堆疊遞迴結構的GPU之中。

鑑於KD-Tree所具有的上述優良特性，本文在實現中也採用了KD-Tree的結構來對空間場景進行劃分。

1.2 KD-Tree的建立

KD-Tree的建立過程是一個自頂向下的遞迴過程，從根結點開始執行向下的空間劃分，空間劃分過程中最主的操作就是對分割平面的選取。KD-Tree中各結點的分割平面

相對於八叉樹、均勻分割等劃分結構的分割平面增加了一個自由度，但相對於BSP分割中的任意方向的分割平面卻又降低了一個自由度。KD-Tree的分割平面均是軸對齊的，

這樣就可以直接確度分割平面的法向量，接下來主要做的就是對此有向平面在軸對齊方向上進行定位。而這裡對分割平面進行定位的基本原則即是使得到的整棵KD-Tree儘可

能的平衡，這也就要求將當前結點中的幾何體元儘可能均勻地分配到兩個子結點中。對於網格組成的三維場景，這裡的幾何體元主要為三角形，因此現在的問題就轉化為

對當前結點中的三角形的分配問題。

給定一個含有n個三角形的KD-Tree結點，假設需要定位其在X方向上的分割平面。由空間知識可得任意三角形與其可能的分割平面

有三種相對位置關係，即：與平面相交、處於平面前方（相對於其法向）、處於平面後方。對於不相交的這些三角形，在產生子結點時直接分配即可，對於相交的三角形，則需要在產生子結點時進行分割。一個三角形被平面分割後可能產生多個三角形，而且根據分割平面所處的位置不同對三角形的分割方式也不同。如果將這些相交的三角形分割後所得到的子三角形的數目也考慮到分割平面的選取中則增加了很多計算量，而且通過分析可得知，在一個結點中與分割平面相交的三角形數目要少於不相交的三交形數目，因而可以在分割平面的選擇時不考慮這些處於相交位置的三角形的影響。這樣就可以在生成子結點時較快得到分割平面。不過在一個法向量方向上潛在的分割平面又有無數種位置可能，在實踐中只能取一種近似的操作，這裡採用一種常用的方法，即使用幾何體元的AABB包圍盒在分割平面法向上的位置來作為分割平面的潛在位置。這樣既確定的潛在平面的分佈位置，又有了分割平面的選取標準，接下來要做的就是從潛在分割平面中選取一個最優的分割平面。

設當前結點的潛在分割平面集全為，每個分割平面所對應的三角形位置集合為，則最優分割平面pb的選擇可由下式來確定：

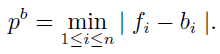
在上式中潛在分割平面的數量為當前結點中三角形數量的2倍速，這是由於每個三角形的AABB在軸對齊的兩端均確定了一個潛在的分割平面。分割平面確定之後即相當於完成了對當前結點的分割操作，接下來要做的就是根據與分割平面的相對位置關係，將三角形或直接或者分割後分配到不同的子結點即可。對當前結點分割完成這後再遞迴地對子結點進行上述操作直到葉子結點。葉子結點的定義也有多種方法，可以是樹建立到一定深度後，此深度之後的結點即為葉子結點，也可以上結點中三角形的數目達到一定數量之後，再少於該數值的結點即為葉子結點。本文中採用的方法是當結點中三角形的數目少於一定數量之後即成為葉子結點，到達葉子結點之後當前分割操作即可停止。

2. 無堆疊的空間二叉樹遍歷

使用空間劃分對三維場景進行有機地合理組織以後，整個場景在抽象上即變成為一樹形結構，而光線與場景的求交加速演算法正得益於這樣的樹形結構可以快速地排除無關結點的影響。基於樹形結構的光線求交演算法也即轉化成為樹的遍歷問題。根據光線跟蹤問題的特點，多數情況下是需要求解與當前光線最近的幾何體元的相交點，因此在空間劃分樹進行遍歷時多采用深度優先遍歷方法。深度優先遍歷方法即是在當前結點同時有子結點和兄弟結點時，其下一步的搜尋物件是其子結點而非兄弟結點。對於樹的遍歷也是一種遞迴結構的呼叫過程，對每個結點均執行相同的操作，這種遍歷演算法在傳統的CPU上實現很容易藉助於堆疊就可以實現這樣的操作。不過在GPU上，由於其無類似的堆疊結構故而也就不支援這樣的遞迴呼叫操作，因此對空間二叉樹的遍歷就不能採用傳統的遞迴呼叫方法來實現。在本文中使用一種無堆疊的方法來實現GPU平臺的空間二叉樹遍歷。

2.1 無堆疊解決方案

本文中的無堆疊解決方法其實也可以理解為模擬堆疊的解決方法。由於在對空間分割樹進行遍歷過程中採用了深度優先搜尋，因此對於搜尋路徑的選取就存在一個由當前結點向上回溯的過程，即需要不斷的由子結點向上尋找到其相應的父結點。在CPU的堆疊中可以方便的利用遞迴特性，依次將父結點子結點入棧，這樣在退出子結點之後，接著出棧即可得到相應的父結點。而在GPU上無法利用硬體這樣實現，但卻可以模擬這樣的一個過程，建立一個類堆疊的結構，通過使用一些變數來記錄一些資料，從而來記錄當前搜尋的路徑，在向上回溯時利用已有的路徑求得待搜尋的路徑。比如在當前結點處，我們可以使用一組資料來當前結點的標號，子結點的狀態等來儲存當前搜尋的方向，如果它的一個孩子的狀態為已經遍歷過，則在回溯到此結點時則不需要再向該子結點搜尋，對其它的子結點做同樣的操作即可模擬地實現回深度優先搜尋的效果。

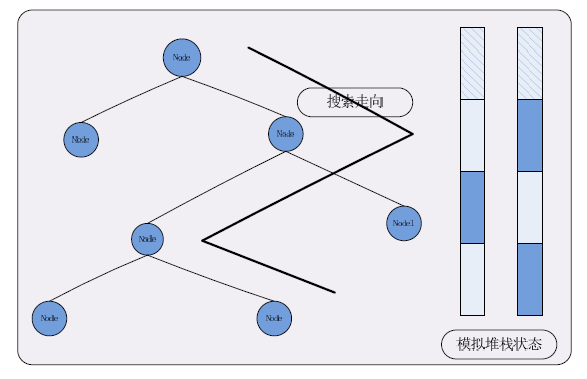
圖1. 在對空間二叉樹進行無堆疊遍歷過程的操作示意圖。

2.2 具體實現細節

空間樹無堆疊遍歷的主要實現策略是建立虛擬的類堆疊結構來記錄結點的資訊，從而實現控制遍歷的走向。我們需要對每個結點記錄相應的狀態，在遍歷中對於每個結點也只有兩種狀態：已遍歷過、末遍歷過，互斥的兩種狀態很容易使用開關值來進行標記。同時對於二叉樹來說，每個結點又最多有兩個子結點，故而在當前結點上的遍歷方向也最多有兩種狀態。這樣歸結下來就可以得到對於每個結點需要兩個開關值來記錄遍歷過程在此結點處的走向。對於開關值最節省空間，且判斷效率較高的一種表示方法即是使用位來表示，而且對場景劃分得到的二叉樹的深度有限，因而可以在預測範圍內使用一定字長的變數來表示一個一定深度的二叉樹遍歷模擬堆疊。基於GPU的無堆疊空間劃分二叉樹的遍歷主要以下述方法實現：使用兩個int來表示兩個深度為64的模擬堆疊，每個模擬堆疊中的每一位記錄當前結點的了個子結點的狀態，通過在當前結點處從模擬堆疊中通過位操作來得到其子結點的狀態，從而控制遍歷的方向而實現深度搜索或是向上回溯。

3. 基於GPU的加速光線跟蹤演算法

光線跟蹤是計算機圖形學領域的經典演算法，它主要是模擬現實現世界中的成像原理，通過對每個畫素進行著色。這其中主要涉及以下個問題：光線如何傳遞、光線傳遞到什麼位置中止、光線所得到著色值。光照到達物體表面時，物體會對光發生反射、透射、吸收和折射等，對所有這些情況進行處理涉及複雜的光照模型。在本文中為了抽象並簡化問題的實現，使用了當前在硬體渲染管線中所主要採用的Phong光照模型。它主要在光線與場景的交點處根據物體的材質計算相應的specular、diffuse值來確定畫素的顏色值。光線跟蹤的過程就是從螢幕中的畫素點出發，計算該點處光線的方向，然後在此方向上對場景進行遍歷然後進行著色計算，這裡主要有兩個問題：1. 光線的產生問題，2. 光線與場景的碰撞檢測問題。傳統的於CPU上實現的光線跟蹤演算法對於這兩個問題只能序列地進行處於，首先，對於每條光線，生成光線的基本引數，然後利用空間劃分結構與此條光線進行碰撞檢測，最後在碰撞點對畫素進行著色。對於折射及反射效果則只需要碰撞點再進行二、三級光線的生成，並重覆上述的著色過程，最後對原始畫素進行著色效果的疊加，最後即可以得到具有反射、折射效果的高質量渲染影象。由上述分析可知，對於每個畫素進行著色時，不存在畫素間的依賴，即在當前層的光線中不存在依賴，因而這就具有很好的並行性。而光線跟蹤與GPU平臺上的並行化實現也下在是利用這一併行特性而進行高效的實現。

並行化的GPU光線跟蹤演算法結構如下圖所示：

圖2. 基於GPU的並行化光線跟蹤演算法結構。

總體來說，光線跟蹤在GPU上的實現主要有以下幾個並行部分：

1. 對於光線生成的GPU並行化。這裡對每個光線均獨立地生成相應的基本引數。

2. 對於光線與場景碰撞檢測及著色過程的並行化。由於同一層的光線之間在著色時並沒有相素依賴關係，因而就可以並行地對每一條光線進行處理。

4. 優化細節

使用上述演算法實現基於GPU的光線跟蹤演算法以後，可以根據具體的需求對演算法進行再優化，這裡主要涉及一些細節方面的優化。雖然演算法的整體效率是由演算法的架構來決定，

不過通過對細節上的優化也可以在很大程度上提升演算法的執行效率，特別是專門針對GPU架構的有針對性的優化操作。

1. 在KD-Tree建立時，首先採用均勻分割，當三角形數目達到一定數量時採用最優分割面的選取分割，這樣可以提高KD-Tree建立的效率。

2. 將KD-Tree資訊、場景原始幾何資料，分別歸類存放於不同紋理之中，通過紋理參照在需要進行同型別資料的訪問。這樣一方面可以利用紋理提供的虛擬cache提高資料訪問時的效率，另一方面相關資料的打包存放又減少了相同資料的重複訪問次數，減少了訪問的延時。

5. 實驗結果與結論

最後在實現上述演算法並進行相應細節上的優化操作之後，通過實驗對演算法的整體效能進行了測試。實驗時所採用的PC平臺為Windows 32位作業系統，處理器和記憶體為：Intel Core Duo CPU 2.8GHz， RAM 2.0GB，所使用的顯示卡GPU支援為GTX 260。演算法的核心部分在GPU版本與CPU版本均做相同的操作，並且均對程式碼進行了相就應的優化。對於幾個典型測試場景的光線跟蹤效果圖片見於下圖所示：

圖3. 對幾種典型場景進行基於GPU的光線跟蹤所得到渲染結果，從圖中可以看出使用基於GPU的光線跟蹤演算法可以得到較高質量的渲染效果。

如圖所示，可見利用GPU的高效浮點運算能力可以得到高質量的渲染影象。而且演算法最重要的是相對於傳統CPU上的光線跟蹤演算法有重要的效能提升，通過對渲染時間進行測試，統計得到如下的演算法執行進間與加速比：

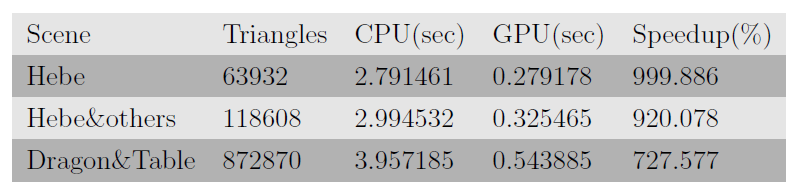
表1. 對幾個典型場景進行渲染測試所得到時間列表。測試進所使用的GPU平臺為GTX 260，從上表中可以看出將演算法合理並行化後移植於GPU平臺得到了樂觀的加速比。

通過實驗說明合理地對光線跟蹤演算法進行並行化後，利用CUDA提供的GPU高效加速運算效果可以顯著地提高傳統的光線跟蹤演算法的效果，這也為這一經典、但卻耗費大量運算資源的經典演算法注入了新的生命活力。

6. 將來的工作

將光線跟蹤演算法在GPU上進行高效地實現為GPU的推廣和應用提供了有力的支援，在將來的工作中針對光線跟蹤及其它圖形學領域的渲染演算法實現與改進將主要集中於以下幾個方面：

1. 針對GPU資料存取的延時問題，雖然通過利用texture的存取方式可以在一定程度上解決這個問題，不過延時仍然限制了演算法的效率。一種解決方法就是對光線進行pcaket打包，這樣對於一種光線的遍歷就可以擴充套件為同時對多條光線的遍歷，這樣就節省了反覆對存global memory中的大量資料訪問，從而提升演算法的執行效率。

2. 由於GPU對大量資料通過紋理的方式進行訪問可以得到硬體的虛擬cache的支援來提高訪問效率，因此更好地利用這一特性就可以減少執行的延時。通過分析可以得到如果相鄰的光線之間的關聯性較大，即相鄰的光線之間在KD-Tree中的遍歷路線大致相同時，這樣就要在相鄰的光線遍歷KD-Tree時合理地重用一些資源，這樣就也提高了效率。將來工作的一方面就是研究這樣的一個問題，通過對光線進行再分析，而實現更合理地有機組織，比如對光線根據方向進行一種排序，從而提高演算法的效率。

3. 利用GPU的高並行處理特性，在將來的研究與實踐工作中將嘗試將更多的計算機圖形學領域的演算法利用CUDA來進行加速，如光子對映、輻射度演算法等基於物理的經典、大耗時演算法。