參考

概述

是一種平衡二叉樹，在每個節點儲存一條線段（一個數組區間），主要用於高效解決連續區間的動態查詢，基本能保持每個操作的複雜度為O（logn）。

例子

問題描述：從陣列arr[0…n-1]中查詢某個區間內的最小值，其中陣列大小固定，但是陣列中的元素的值隨時可以更新。

最簡單的解法：遍歷陣列區間找到最小值，時間複雜度O（n），額外空間複雜度O（1）儲存臨時min變數，但當資料很多，查詢操作頻繁時，可能超時。

快一點的解法：使用二維陣列儲存提前計算好的區間[i, j]內的最小值，預處理時間為O(n2)，查詢耗時O（1），但是需要額外的O(n2)空間，當資料量很大時，空間消耗龐大，而且改變了資料中的某一個值時，更新二維陣列中的最小值也很麻煩。

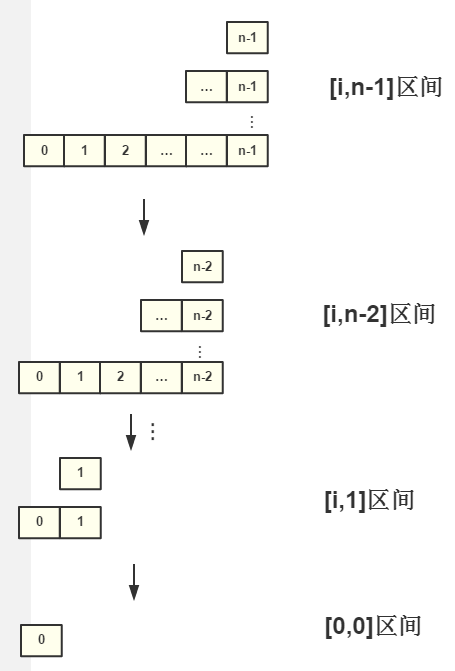
用線段樹的解法：預處理耗時O（n），查詢、更新操作O（logn），需要額外的空間O（n）。根據這個問題構造如下的二叉樹：

• 葉子節點是原始陣列arr中的元素
• 非葉子結點代表它的所有孩子節點構成區間的最小值

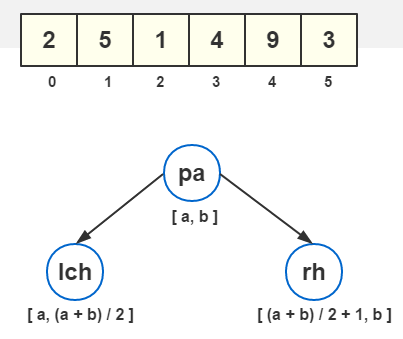
例如對於陣列[2, 5, 1, 4, 9, 3]可以構造如下的二叉樹（黑線條為葉子節點，藍線條為非葉子節點，為對應陣列區間的最小值）例如根節點表示陣列區間arr[0…5]內的最小值是1：

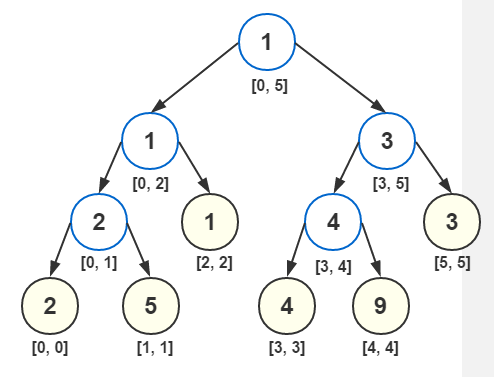
對於包含n個葉子節點的平衡二叉樹，有n-1個非葉子結點，因此一共有2n-1個節點，因此儲存線段需要的空間複雜度是O（n）。