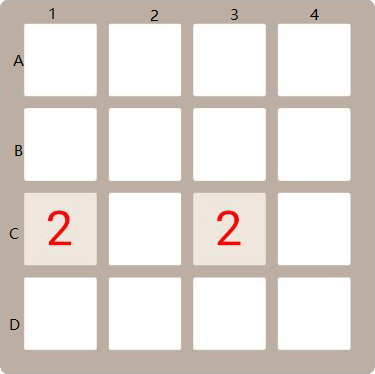
2048遊戲回顧二:演算法總結(移動、合併、動畫等)
如果只是單純的寫一個2048遊戲,讓這個遊戲可以玩的話,工作量還是蠻小的。不過,在這寫工作中,你可能花時間最多的就是數字的移動與合併的演算法了,如果沒有做過,可能確實要花點時間來構思,所以,寫完2048遊戲以後,我希望能把它做個記錄。
移動與合併的演算法
比如說我們有如下一個介面:
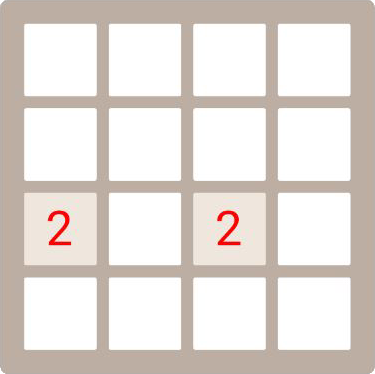
現在,玩家向左劃,這個導致所有的數字向左移動,並且移動的過程中如果發生碰撞,會檢查數字是不是可以合併。
我們的演算法應該是通用的,不僅對於4*4模式,即便是針對3*3模式,n*n模式,它都應該是一樣的。
那麼怎麼做呢?其實就兩步:
第一步:把第一個空格和空格後面的第一個數字(如果有)交換。
第二步:交換後檢查需不需要合併。
以此類推。
為了便於陳述,我們給圖片做一個座標:
在這張圖片中,按照我們說的,第一個空白和第一個數字交換,也就是把(2,C)和(3,C)交換,交換後檢查能不能合併,如果能則合併,不過不能則不合並,這裡顯然可以合併,所以我們把他們合併為4.然後空白後面就沒有數字了,演算法結束。
因此,我們的演算法必須記錄第一個空白的位置和第一個數字的位置,那麼我們用k記錄空白,用j記錄第一個數字,然後對於每一行,從左向右做這樣的事情。
直接上程式碼吧,結合程式碼一說就會明白:
首先,我們的一個數字使用一個Number類來表述:
public class Number {
public int mScores;
public int 可見一個Number中有scores,也就是分數,當前的位置和之前的位置是用來計算動畫的,我們需要把一個Number從之前的位置移動到當前的位置。
然後整個遊戲使用一個Numbers類來表述:
public class Numbers {
Number [][] mNumbers = new Number[Game2048StaticControl.gamePlayMode][Game2048StaticControl.gamePlayMode];
public Numbers(){
for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
mNumbers[i][j] = new Number(0,0);
}
}
}
public Number getNumber(int x,int y){
return mNumbers[x][y];
}
public Number [][] getNumbers (){
return mNumbers;
}
public int getBlankCount(){
int count = 0;
for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
if(mNumbers[i][j].mScores==0){
count++;
}
}
}
return count;
}
public int getPositonFromBlankCountTh(int blankTh){
int count = 0;
for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
if(mNumbers[i][j].mScores==0){
if(count==blankTh){
return i*Game2048StaticControl.gamePlayMode+j;
}else {
count++;
}
}
}
}
return -1;
}
public void swapNumber(int position1,int position2){
mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode].mCurPosition = position2;
mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode].mBeforePosition = position1;
mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode].mCurPosition = position1;
mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode].mBeforePosition = position2;
Number tem = mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode];
mNumbers[position1/Game2048StaticControl.gamePlayMode][position1%Game2048StaticControl.gamePlayMode] = mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode];
mNumbers[position2/Game2048StaticControl.gamePlayMode][position2%Game2048StaticControl.gamePlayMode] = tem;
}
}這個類的核心就是一個Number [n][n]的陣列,n可以為任意值,因為我們的演算法是通用的。
有了這個的概念以後,我們來看向左移動的演算法,思想前面已經講過了,直接看程式碼,結合程式碼非常容易理解。
//return 0:do nothing
//return 1:move
//return 2:combine
public int leftKeyDealAlgorithm(){
int i, j, k;
boolean isMoved = false;
boolean isFinalMove = false;
boolean isFinalCombie = false;
for(i=0;i<Game2048StaticControl.gamePlayMode;i++){
j=k=0;
isMoved = false;
while (true) {
while (j<Game2048StaticControl.gamePlayMode && !isPosionHasNumber(i,j))
j++;
if (j > Game2048StaticControl.gamePlayMode-1)
break;
if (j > k){
isMoved = true;
isFinalMove = true;
Number number = getNumber(i,j);
number.isNeedMove = true;
number.isNeedCombine = false;
swapNumber(i*Game2048StaticControl.gamePlayMode+k,i*Game2048StaticControl.gamePlayMode+j);
}
if (k > 0 && getNumber(i,k).mScores==getNumber(i,k-1).mScores && !getNumber(i,k-1).isNeedCombine){
isFinalCombie = true;
Number numberk = getNumber(i,k);
Number numberkl = getNumber(i,k-1);
if(isMoved){
numberkl.mBeforePosition = numberk.mBeforePosition;
}else {
numberkl.mBeforePosition = i*Game2048StaticControl.gamePlayMode+k;
}
numberkl.mCurPosition = i*Game2048StaticControl.gamePlayMode+k-1;
numberkl.isNeedMove = true;
numberkl.isNeedCombine = true;
numberkl.mScores <<=1;
updateCurScoresAndHistoryScores(numberkl.mScores);
numberk.reset();
numberk.mCurPosition = numberk.mBeforePosition = i*Game2048StaticControl.gamePlayMode+k;
} else{
k++;
}
j++;
}
}
return isFinalCombie?2:(isFinalMove?1:0);
}
第一步:j=k=0;
第二步:找到第一個數字:
while (j<Game2048StaticControl.gamePlayMode && !isPosionHasNumber(i,j))
j++;第三步:如果j > k,那就意味這k這個位置的數字一定是空的,j這個位置的一定是第一個數字,所以就把他們交換。
第四步:判斷是不是需要合併
if (k > 0 && getNumber(i,k).mScores==getNumber(i,k-1).mScores && !getNumber(i,k-1).isNeedCombine判斷的條件是k>0,因為是向前合併,所以合併至少是從第二個開始的,其次就是兩個數字要相等,同時,已經合併了得數字不能再合併。
然後再做下一個迴圈,如此往復即可完成。
下面貼出其他三個方向的程式碼。
public int rightKeyDealAlgorithm(){
int i, j, k;
boolean isMoved = false;
boolean isFinalMove = false;
boolean isFinalCombie = false;
for(i=0;i<Game2048StaticControl.gamePlayMode;i++){
j=k=Game2048StaticControl.gamePlayMode-1;
isMoved = false;
while (true) {
while (j>-1 && !isPosionHasNumber(i,j))
j--;
if (j < 0)
break;
if (j < k){
isMoved = true;
isFinalMove = true;
Number number = getNumber(i,j);
number.isNeedMove = true;
number.isNeedCombine = false;
swapNumber(i*Game2048StaticControl.gamePlayMode+k,i*Game2048StaticControl.gamePlayMode+j);
}
if (k < Game2048StaticControl.gamePlayMode-1 && getNumber(i,k).mScores==getNumber(i,k+1).mScores && !getNumber(i,k+1).isNeedCombine){
isFinalCombie = true;
Number numberk = getNumber(i,k);
Number numberkl = getNumber(i,k+1);
if(isMoved){
numberkl.mBeforePosition = numberk.mBeforePosition;
}else {
numberkl.mBeforePosition = i*Game2048StaticControl.gamePlayMode+k;
}
numberkl.mCurPosition = i*Game2048StaticControl.gamePlayMode+k+1;
numberkl.isNeedMove = true;
numberkl.isNeedCombine = true;
numberkl.mScores <<=1;
updateCurScoresAndHistoryScores(numberkl.mScores);
numberk.reset();
numberk.mCurPosition = numberk.mBeforePosition = i*Game2048StaticControl.gamePlayMode+k;
} else{
k--;
}
j--;
}
}
return isFinalCombie?2:(isFinalMove?1:0);
}
public int upKeyDealAlgorithm(){
int i, j, k;
boolean isMoved = false;
boolean isFinalMove = false;
boolean isFinalCombie = false;
for(i=0;i<Game2048StaticControl.gamePlayMode;i++){
j=k=0;
isMoved = false;
while (true) {
while (j<Game2048StaticControl.gamePlayMode && !isPosionHasNumber(j,i))
j++;
if (j > Game2048StaticControl.gamePlayMode-1)
break;
if (j > k){
isMoved = true;
isFinalMove = true;
Number number = getNumber(j,i);
number.isNeedMove = true;
number.isNeedCombine = false;
swapNumber(k*Game2048StaticControl.gamePlayMode+i,j*Game2048StaticControl.gamePlayMode+i);
}
if (k > 0 && getNumber(k,i).mScores==getNumber(k-1,i).mScores && !getNumber(k-1,i).isNeedCombine){
isFinalCombie = true;
Number numberk = getNumber(k,i);
Number numberkl = getNumber(k-1,i);
if(isMoved){
numberkl.mBeforePosition = numberk.mBeforePosition;
}else {
numberkl.mBeforePosition = k*Game2048StaticControl.gamePlayMode+i;
}
numberkl.mCurPosition = (k-1)*Game2048StaticControl.gamePlayMode+i;
numberkl.isNeedMove = true;
numberkl.isNeedCombine = true;
numberkl.mScores <<=1;
updateCurScoresAndHistoryScores(numberkl.mScores);
numberk.reset();
numberk.mCurPosition = numberk.mBeforePosition = k*Game2048StaticControl.gamePlayMode+i;
} else{
k++;
}
j++;
}
}
return isFinalCombie?2:(isFinalMove?1:0);
}
public int downKeyDealAlgorithm(){
int i, j, k;
boolean isMoved = false;
boolean isFinalMove = false;
boolean isFinalCombie = false;
for(i=0;i<Game2048StaticControl.gamePlayMode;i++){
j=k=Game2048StaticControl.gamePlayMode-1;
isMoved = false;
while (true) {
while (j>-1 && !isPosionHasNumber(j,i))
j--;
if (j < 0)
break;
if (j < k){
isMoved = true;
isFinalMove = true;
Number number = getNumber(j,i);
number.isNeedMove = true;
number.isNeedCombine = false;
swapNumber(k*Game2048StaticControl.gamePlayMode+i,j*Game2048StaticControl.gamePlayMode+i);
}
if (k < Game2048StaticControl.gamePlayMode-1 && getNumber(k,i).mScores==getNumber(k+1,i).mScores && !getNumber(k+1,i).isNeedCombine){
isFinalCombie = true;
Number numberk = getNumber(k,i);
Number numberkl = getNumber(k+1,i);
if(isMoved){
numberkl.mBeforePosition = numberk.mBeforePosition;
}else {
numberkl.mBeforePosition = k*Game2048StaticControl.gamePlayMode+i;
}
numberkl.mCurPosition = (k+1)*Game2048StaticControl.gamePlayMode+i;
numberkl.isNeedMove = true;
numberkl.isNeedCombine = true;
numberkl.mScores <<=1;
updateCurScoresAndHistoryScores(numberkl.mScores);
numberk.reset();
numberk.mCurPosition = numberk.mBeforePosition = k*Game2048StaticControl.gamePlayMode+i;
} else{
k--;
}
j--;
}
}
return isFinalCombie?2:(isFinalMove?1:0);
}動畫
計算結束以後,我們需要使用動畫移動和合並數字,因為都是直線運動,所以動畫並不複雜,想想我們的Number類,計算動畫只需要兩個變數,一個之前的位置,一個是當前的位置。
我們可以理一下思路:當用戶需要向左移動時:
case Game2048StaticControl.DIRECT_LEFT:{
mNumberQueue.pushItem(mGAM.getmNumbers());
int ret = mGAM.leftKeyDealAlgorithm();
if (ret>0){
startAnimation(mHolder,mPaint,Game2048StaticControl.DIRECT_LEFT);
mGAM.updateNumbers();
doDrawGameSurface();
sendEmptyMessage(Game2048StaticControl.GENERATE_NUMBER);
playSoundEffect(ret);
}
break;
}我們需要做如下幾步:
第一步:儲存當前的遊戲,用於反悔的時候回退。mNumberQueue.pushItem(mGAM.getmNumbers())
第二步:計算移動與合併
mGAM.leftKeyDealAlgorithm();
第三步:使用動畫移動和合並數字
startAnimation(mHolder,mPaint,Game2048StaticControl.DIRECT_LEFT);
第四步:生成一個新的數字
sendEmptyMessage(Game2048StaticControl.GENERATE_NUMBER);
通過傳送訊息來實現,具體的實現在訊息的處理程式碼中,這很簡單,這裡暫不展開。
下面看一個startAnimation方法。
startAnimation定義如下:
public void startAnimation(SurfaceHolder holder,Paint paint,int direct){
int count = 0;
RectF rectF = new RectF();
while (count++<Game2048StaticControl.ANIMATION_MOVE_STEP) {
Canvas canvas = holder.lockCanvas();
mDrawTools.initSurfaceBg(canvas, paint);
mDrawTools.drawSurfaceMap(canvas, paint);
mDrawTools.drawSurfaceMapAndNumbersWhoIsNeedCombine(canvas,paint);
for (int i = 0; i < Game2048StaticControl.gamePlayMode; i++) {
for (int j = 0; j < Game2048StaticControl.gamePlayMode; j++) {
mGAM.aniInsertValue(i, j, count, Game2048StaticControl.ANIMATION_MOVE_STEP,direct,rectF);
if(rectF != null && mGAM.isPosionHasNumber(i,j) && mGAM.getNumber(i,j).isNeedMove){
mDrawTools.drawNumberByRectF(i,j,canvas,paint,rectF);
}
}
}
holder.unlockCanvasAndPost(canvas);
}
}就是對每一個Number,使用 mGAM.aniInsertValue方法來計算它的座標:
public void aniInsertValue(int x,int y,int count,int insertCount,int direct,RectF rectF){
Number number = getNumber(x,y);
if(number.mCurPosition == number.mBeforePosition){
return;
}
float xDiffPixels = Game2048StaticControl.GameNumberViewPosition[number.mCurPosition/Game2048StaticControl.gamePlayMode]
[number.mCurPosition%Game2048StaticControl.gamePlayMode].left
-Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].left;
float yDiffPixels = Game2048StaticControl.GameNumberViewPosition[number.mCurPosition/Game2048StaticControl.gamePlayMode]
[number.mCurPosition%Game2048StaticControl.gamePlayMode].top
-Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].top;
xDiffPixels = Math.abs(xDiffPixels);
yDiffPixels = Math.abs(yDiffPixels);
float xStep = xDiffPixels/insertCount;
float yStep = yDiffPixels/insertCount;
float xNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mCurPosition/Game2048StaticControl.gamePlayMode]
[number.mCurPosition%Game2048StaticControl.gamePlayMode].left;
float yNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mCurPosition/Game2048StaticControl.gamePlayMode]
[number.mCurPosition%Game2048StaticControl.gamePlayMode].top;;
switch (direct){
case DIRECT_UP:{
yNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].top
- yStep*count;
break;
}
case DIRECT_DOWN:{
yNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].top
+ yStep*count;
break;
}
case DIRECT_LEFT:{
xNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].left
- xStep*count;
break;
}
case DIRECT_RIGHT:{
xNewPosition = Game2048StaticControl.GameNumberViewPosition[number.mBeforePosition/Game2048StaticControl.gamePlayMode]
[number.mBeforePosition%Game2048StaticControl.gamePlayMode].left
+ xStep*count;
break;
}
default:break;
}
rectF.set(xNewPosition,yNewPosition,xNewPosition+Game2048StaticControl.gameNumberViewLength
,yNewPosition+Game2048StaticControl.gameNumberViewLength);
}計算的過程正對上下左右各不相同,原理非常簡單:
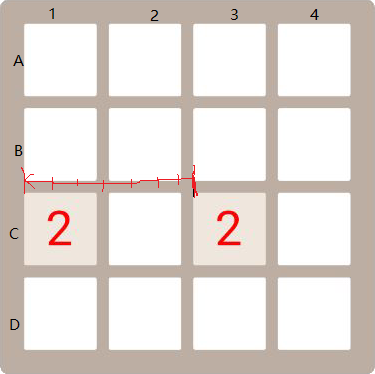
原理就是在途中的花點的地方繪製一下數字就好了。也就是所謂的線性插值法。
在隨機位置隨機生成2或者4
生成2或者4就太簡單了,隨機位置怎麼計算呢?這裡要注意實在空白方格的隨機位置哦,因此首先要獲取當前有多少個空格:
public int getBlankCount(){
return mNumbers.getBlankCount();
}進一步:
public int getBlankCount(){
int count = 0;
for(int i=0;i<Game2048StaticControl.gamePlayMode;i++){
for(int j=0;j<Game2048StaticControl.gamePlayMode;j++){
if(mNumbers[i][j].mScores==0){
count++;
}
}
}
return count;
}比如說當前有7個空白處,那麼就只能生7以內的隨機數n,然後 把它插到第n個空白處。
插入方法如下:
public int setOneRandomNumberInRandomPosition(){
int scores = Game2048Algorithm.getRandom2Or4();
int blankCount = getBlankCount();
Log.d(TAG,"blankCount:"+blankCount);
int blankTh = 0;
if(blankCount<=0){
return -1;
}else{
blankTh = Game2048Algorithm.getRandomPosition(blankCount);
}
int position = mNumbers.getPositonFromBlankCountTh(blankTh);
if (position<0){
Log.d(TAG,"getPositonFromBlankCountTh return error");
return -1;
}
Number num = mNumbers.getNumber(position/Game2048StaticControl.gamePlayMode,position%Game2048StaticControl.gamePlayMode);
num.mScores = scores;
num.mBeforePosition = num.mCurPosition = position;
num.isNeedCombine = num.isNeedMove = false;
return position;
}檢測遊戲失敗
檢測遊戲的失敗也有一個通用的方式:
public boolean checkGameOver(){
Log.d(TAG,"checkGameOver");
for (int i = 0; i < Game2048StaticControl.gamePlayMode; i++)
{
for (int j = 0; j < Game2048StaticControl.gamePlayMode; j++)
{
if (j != Game2048StaticControl.gamePlayMode-1 && getNumber(i,j).mScores == getNumber(i,j+1).mScores)
return false;
if (i != Game2048StaticControl.gamePlayMode-1 && getNumber(i,j).mScores == getNumber(i+1,j).mScores)
return false;
}
}
if (mListener!=null){
mListener.onGameOver();
}
return true;
}演算法的核心思想就是一定要對每一個數字對比它的前後左右。只要發現有相等的就認為可以繼續。當然,判斷的前提的空白格子的數量為0。