題目背景

大家都知道，基因可以看作一個堿基對序列。它包含了44種核苷酸，簡記作A,C,G,TA,C,G,T。生物學家正致力於尋找人類基因的功能，以利用於診斷疾病和發明藥物。

在一個人類基因工作組的任務中，生物學家研究的是：兩個基因的相似程度。因為這個研究對疾病的治療有著非同尋常的作用。

題目描述

兩個基因的相似度的計算方法如下：

對於兩個已知基因，例如AGTGATGAGTGATG和GTTAGGTTAG，將它們的堿基互相對應。當然，中間可以加入一些空堿基-，例如：

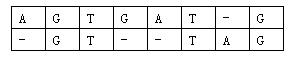
這樣,兩個基因之間的相似度就可以用堿基之間相似度的總和來描述，堿基之間的相似度如下表所示：

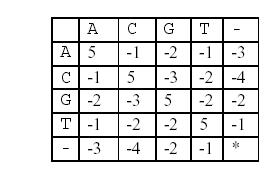
那麽相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9(−3)+5+5+(−2)+(−3)+5+(−3)+5=9。因為兩個基因的對應方法不唯一，例如又有：

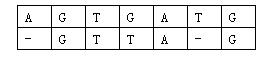
相似度為：(-3)+5+5+(-2)+5+(-1)+5=14(−3)+5+5+(−2)+5+(−1)+5=14。規定兩個基因的相似度為所有對應方法中，相似度最大的那個。

輸入輸出格式

輸入格式：

共兩行。每行首先是一個整數，表示基因的長度；隔一個空格後是一個基因序列，序列中只含A,C,G,TA,C,G,T四個字母。1 \le1≤序列的長度\le 100≤100。

輸出格式：

僅一行，即輸入基因的相似度。

輸入輸出樣例

7 AGTGATG
5 GTTAG

14

其實本蒟蒻以前做過DP題 但是這是第一次自己構造DP方程並且AC

對於我來說這個題的難點在於判斷是誰插誰= =（聽著好奇怪

對於每一個f[i][j]

1. 可以由f[i][j-1]轉移而來
2. 可以由f[i-1][j]轉移而來
3. 可以由f[i-1][j-1]轉移而來

現在來討論每一種情況

• f[i][j-1]轉移

　　新來的b[j]要與一個空堿基匹配

　　相當於在A串上插了一個空堿基 並與B[j]進行匹配 f[i][j] = f[i][j-1] + trs[b[j][0];

• f[i-1][j]轉移

　　新來的a[i]要與一個空堿基匹配

　　f[i][j] = f[i-1][j] + trs[a[i]][0];

• f[i-1][j-1]轉移

　　相互匹配 f[i][j] =f[i-1] [j-1] + trs[a[i]][b[j]];

所以構造完成 循環順序普通即可（想思考也可以想一下）

那麽邊界？可以想到f[i][0] =f[i-1][0] + trs[a[i]][0];

b也同理

分析完啦 上代碼：

#include<bits/stdc++.h>
using namespace std;
int f[105][105];
int a[105],b[105],len2,len1;
int main(){
    const int trs[5][5]=
    {
         {0,-3,-4,-2,-1},
         {-3,5,-1,-2,-1},
         {-4,-1,5,-3,-2},
         {-2,-2,-3,5,-2},
         {-1,-1,-2,-2,5}
     };
    cin>>len1;
    for(int i=1;i<=len1;i++){
        char tra1;
        cin>>tra1;
        if(tra1==‘A‘) a[i] = 1;
        if(tra1==‘C‘) a[i] = 2;
        if(tra1==‘G‘) a[i] = 3;
        if(tra1==‘T‘) a[i] = 4;
    }
    cin>>len2;
    for(int i=1;i<=len2;i++){
        char tra1;
        cin>>tra1;
        if(tra1==‘A‘) b[i] = 1;
        if(tra1==‘C‘) b[i] = 2;
        if(tra1==‘G‘) b[i] = 3;
        if(tra1==‘T‘) b[i] = 4;
    }
    for(int i=1;i<=len1;i++){
        for(int j=1;j<=len2;j++){
            f[i][j] = -0x3f3f3f3f;
        }
    }
    f[0][0] = 0;
    for(int i=1;i<=len1;i++){
        f[i][0] = f[i-1][0] + trs[a[i]][0];
    }
    for(int i=1;i<=len2;i++){
        f[0][i] = f[0][i-1] + trs[0][b[i]];
    }
    
    for(int i=1;i<=len1;i++){
        for(int j=1;j<=len2;j++){
            f[i][j] = max(f[i-1][j-1] + trs[a[i]][b[j]] ,f[i][j]);
            f[i][j] = max(f[i-1][j] + trs [a[i]] [0], f[i][j]);//這裏剛開始一直沒有想清楚嗚嗚嗚嗚嗚
            f[i][j] = max(f[i][j-1] + trs [0] [b[j]], f[i][j]);
        }
    }
    cout<<f[len1][len2]<<endl;
    return 0;
}

真的是好不容易啊 嗚嗚嗚嗚嗚我好弱2節課做了個這SB題；

但是感覺DP思維提升一些 也算沒虧吧

TAG : SIN_XIII ⑨

洛谷P1140 基因匹配 //DP真正意義上的一血