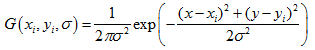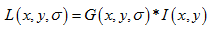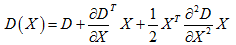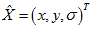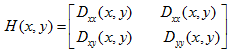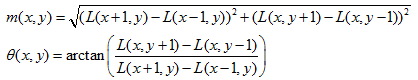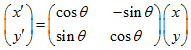原文路徑：https://www.learnopencv.com/histogram-of-oriented-gradients/

按語：偶得SIFT特征匹配算法原理介紹，此文章確通俗易懂，分享之！

1.圖像尺度空間

在了解圖像特征匹配前，需要清楚，兩張照片之所以能匹配得上，是因為其特征點的相似度較高。

而尋找圖像特征點，我們要先知道一個概念，就是“圖像尺度空間”。

平時生活中，用人眼去看一張照片時，隨著觀測距離的增加，圖像會逐漸變得模糊。那麽計算機在“看”一張照片時，會從不同的“尺度”去觀測照片，尺度越大，圖像越模糊。

那麽這裏的“尺度”就是二維高斯函數當中的σ值，一張照片與二維高斯函數卷積後得到很多張不同σ值的高斯圖像，這就好比你用人眼從不同距離去觀測那張照片。所有不同尺度下的圖像，構成單個原始圖像的尺度空間。“圖像尺度空間表達”就是圖像在所有尺度下的描述。

尺度是自然客觀存在的，不是主觀創造的。高斯卷積只是表現尺度空間的一種形式。

2.“尺度空間表達”與“金字塔多分辨率表達”

尺度空間表達——高斯卷積

高斯核是唯一可以產生多尺度空間的核。在低通濾波中，高斯平滑濾波無論是時域還是頻域都十分有效。我們都知道，高斯函數具有五個重要性質：

（1）二維高斯具有旋轉對稱性；

（2）高斯函數是單值函數；

（3）高斯函數的傅立葉變換頻譜是單瓣的；

（4）高斯濾波器寬度(決定著平滑程度)是由參數σ表征的，而且σ和平滑程度的關系是非常簡單的；

（5）二維高斯濾波的計算量隨濾波模板寬度成線性增長而不是成平方增長。

一個圖像的尺度空間L(x,y,σ) ,定義為原始圖像I(x,y)與一個可變尺度的2維高斯函數G(x,y,σ)卷積運算。

二維空間高斯函數表達式：

圖像的尺度空間就是：二維高斯函數與原始圖像卷積運算後的結果，

尺度空間的表達式：

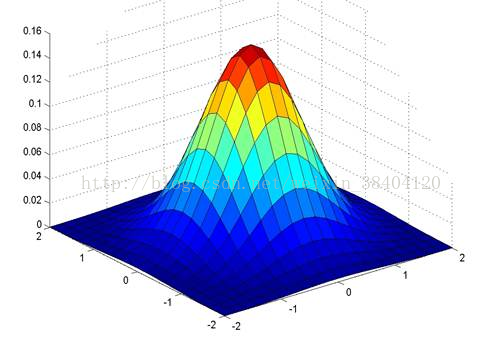
左圖是二維高斯函數在數學坐標系下的圖像。

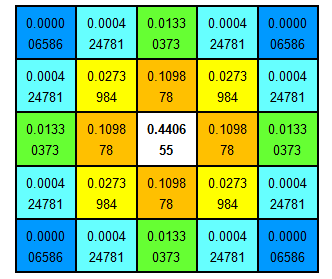
右圖是高斯函數對應的高斯核。

高斯核是圓對稱的，在圖片像素中展現出來的是一個正方形，其大小由高斯模板確定。卷積的結果使原始像素值有最大的權重，距離中心越遠的相鄰像素值權重也越小。

那麽，為什麽要提到高斯模糊與“尺度空間表達”，它們有什麽關系呢？

“尺度空間表達”指的是不同高斯核所平滑後的圖片的不同表達，意思就是：原始照片的分辨率，和經過不同高斯核平滑後的照片的分辨率是一樣的。但是，對於計算機來說，不同模糊程度，照片“看”上去的樣子就不一樣了。高斯核越大，圖片“看”上去就越模糊。

那麽，圖片的模糊與找特征點有關系嗎？

計算機沒有主觀意識去識別哪裏是特征點，它能做的，只是分辨出變化率最快的點。彩色圖是三通道的，不好檢測突變點。需要將RGB圖轉換為灰度圖，此時灰度圖為單通道，灰度值在0~255之間分布。

無論人眼觀測照片的距離有多遠，只要能辨認出物體關鍵的輪廓特征，那就可以大致知道圖像所表達的信息。計算機也一樣，高斯卷積之後，圖像雖然變模糊了。但是整體的像素沒有變，依然可以找到灰度值突變的點。

而這些點，就可以作為候選特征點了，後期再進一步減少點的數量，提高準確率即可。

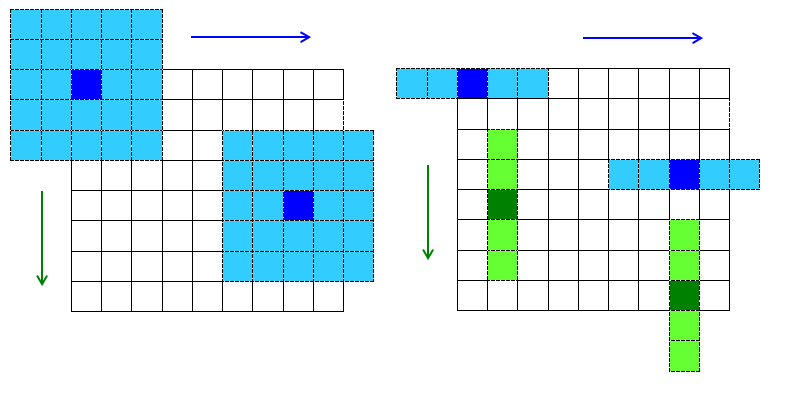
金字塔多分辨率表達——降采樣

這個比較好理解，若對一張圖片進行降采樣，其像素點就會減少，圖片尺寸也會隨之變小。那麽給人的感覺就好比一個金字塔。

所謂圖像金字塔化：就是先進行圖像平滑，再進行降采樣，根據降采樣率不同，所得到一系列尺寸逐漸減小的圖像。

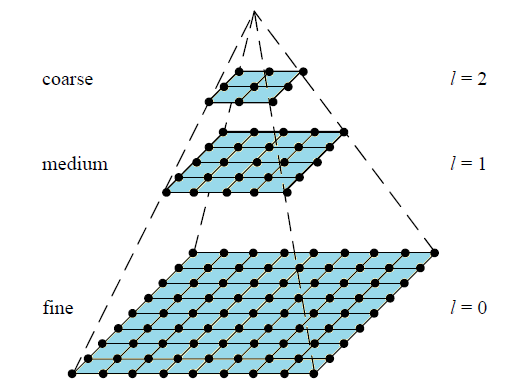
兩種表達的不同之處在於：

“尺度空間表達”在所有尺度上具有相同分辨率，而“圖像金字塔化”在每層的表達上分辨率都會減少固定比率。

“圖像金字塔化”處理速度快，占用存儲空間小，而“尺度空間表達”剛好相反。

3.LOG（Laplassian of Gaussian）

前面提出的那種表達，各有各的優勢：

（1）“尺度空間表達”在所有尺度上具有相同分辨率，而“圖像金字塔化”在每層的表達上分辨率都會減少固定比率。

（2）“圖像金字塔化”處理速度快，占用存儲空間小，而“尺度空間表達”剛好相反。

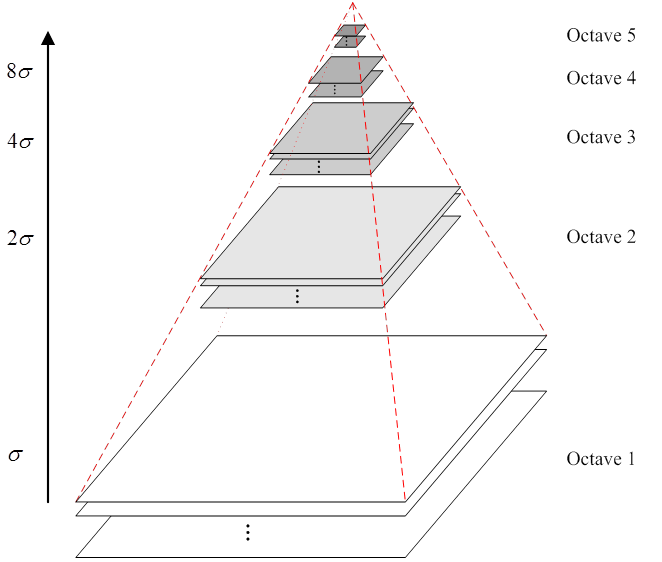
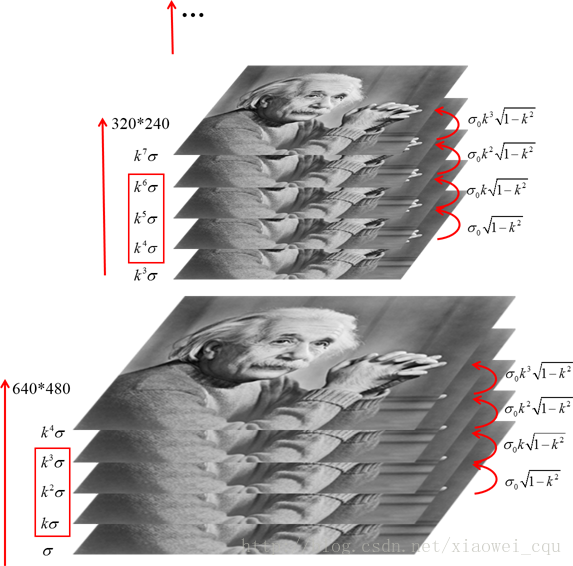
那麽將兩者融合起來的話，就得到了LOG圖像，高斯拉普拉斯變換圖像。其步驟是：先將照片降采樣，得到了不同分辨率下的圖像金字塔。再對每層圖像進行高斯卷積。這樣一來，原本的圖像金字塔每層只有一張圖像，而卷積後，每層又增加了多張不同模糊程度下的照片。

然而，LOG圖像還不是我們想要的，我們做那麽多就是為了更好地獲取特征點，所以還需要對LOG圖像再進一步地優化。所以，DOG圖像橫空出世！！

4.DOG（Difference of Gaussian）

DOG即高斯差分。

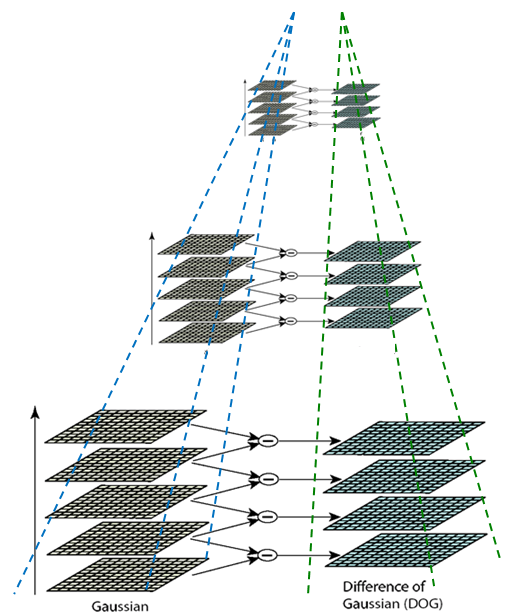
構造高斯差分圖像的步驟是：在獲得LOG圖像後，用其相鄰的圖像進行相減，得到所有圖像重新構造的金字塔就是DOG金字塔。

（左圖是LOG圖像，右圖是DOG圖像）

5.DOG局部極值點

尋找極值點

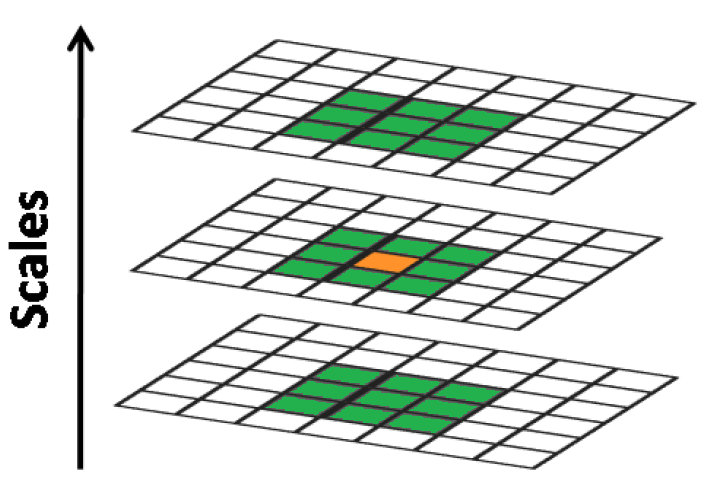
當得到DOG金字塔後，我們接下來要做的是尋找DOG極值點。每個像素點與其周圍的像素點比較，當其大於或者小於所有相鄰點時，即為極值點。

比如說，如下圖所示，以黃點為檢測點，那麽其周圍的點，除了同層所包圍的8個綠點外，還有上一層的9個點與下一層的9個點。

極值點精確定位

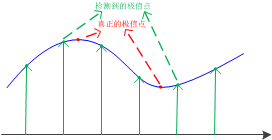
而我們找的的極值點是在高斯差分之後所確定下來的，那麽其是屬於離散空間上的點，不一定是真正意義上的極值點。

我們需用用到一條曲線來進行擬合。

離散轉換為連續，我們會想到泰勒展開式：

則極值點為：

去除邊緣影響

到這一步，得到的極值點是比較精確了，但不夠準確。有些極值點不是我們想要的，當中就有一大部分是邊緣區域產生的極值點。因為物體的邊緣輪廓在灰度圖中，存在著灰度值的突變，這樣的點在計算中就被“誤以為”是特征值。

仔細分析，邊緣區域在縱向上灰度值突變很大，但是橫向上的變化就很小了。好比你用黑筆在白紙上水平畫一條線段。垂直方向看，黑色線與白色區域的突變很大。但是水平方向看時，黑色線上某一點的水平臨近點仍然是黑點，突變程度非常小。

由於這一特殊性質，我們想到了Hessian矩陣，海塞矩陣是用來求曲率的，可以以函數的二階偏導為元素，構成一個2x2的矩陣H：

具體可參見Harris角點檢測算法。

6.方向賦值

經過Harris角點檢測算法之後，基本上得到了我們想要的精確特征點了。接下來我們就要求它們的方向。

在DOG 金字塔中，有很多層高斯模糊後的圖像。在此，我們對其中一張圖像的處理進行說明。當我們精確定位關鍵點後，需要找到該特征點對應的尺度值σ，根據這一尺度值，將對應的高斯圖像的關鍵點進行有限差分，以3×1.5σ為半徑的區域內圖像梯度的幅角和幅值，得到：

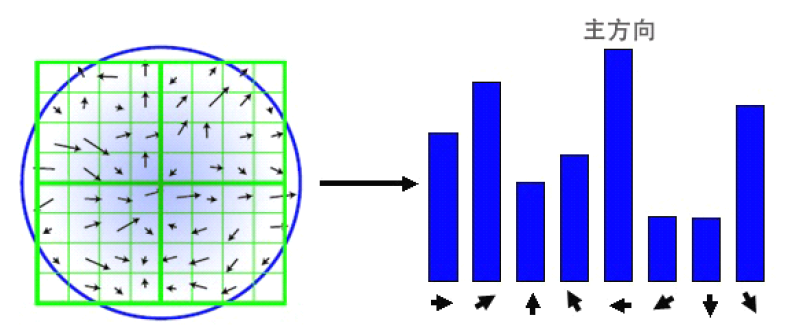
然後利用直方圖統計領域內像素對應的梯度和幅值：梯度方向角為橫軸刻度，取45度為一個單位，那麽橫軸就有8個刻度；縱軸是對應梯度的幅值累加值。

取幅值最高的方向為主方向。有的時候，會出現第二峰值，因為有較多的關鍵點是多方向的。如果直接把它忽略掉不加以考慮的話，最後對匹配精度的影響還是蠻大的。

所以，為了匹配的穩定性，我們將超過峰值能量的百分之80的方向，稱為輔方向。

7.關鍵點描述

確定描述子采樣區域

到了這裏，我們就已經得到賦值後的SIFT特征點了，其包含了位置，尺度，方向的信息。

接下來的要做的是：關鍵點的描述，即用一組向量將關鍵點描述出來。

SIFI 描述子h(x, y,θ)是對特征點附近鄰域內高斯圖像梯度統計結果的一種表示，它是一個三維的陣列，但通常將它表示成一個矢量。矢量是通過對三維陣列按一定規律進行排列得到的。特征描述子與特征點所在的尺度有關，因此，對梯度的求取應在特征點對應的高斯圖像上進行。

生成描述子

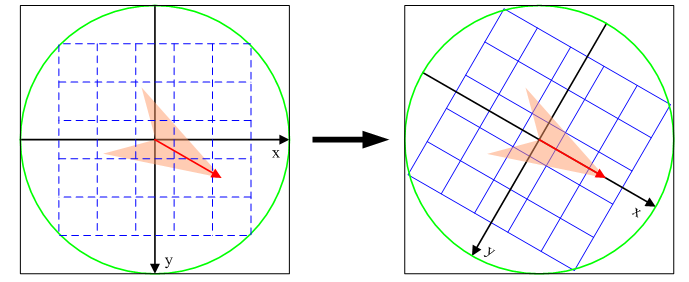
為了保證特征矢量具有旋轉不變性，需要以特征點為中心，將特征點附近鄰域內(mσ(Bp+ 1)√2 x mσ(Bp+ 1)√2)圖像梯度的位置和方向旋轉一個方向角θ，即將原圖像x軸轉到與主方向相同的方向。

旋轉公式如下：

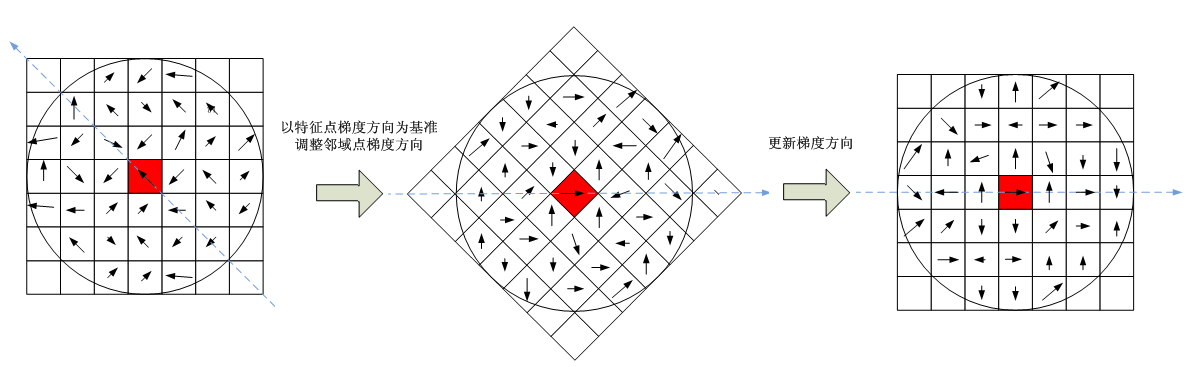
　在特征點附近鄰域圖像梯度的位置和方向旋轉後，再以特征點為中心，在旋轉後的圖像中取一個mσBp x mσBp大小的圖像區域。並將它等間隔劃分成Bp X Bp個子區域，每個間隔為mσ像元。

到這裏，有人會問：旋轉過程中，中圖和右圖為什麽每個像素點的方向不一樣？其實，你要明確一點，你所選的小區域，是關鍵點旋轉後的小區域，右圖的區域跟旋轉前的區域不一樣了，右圖是重新選取得區域，但是區域大小沒變。

接下來就是生成特征匹配點。

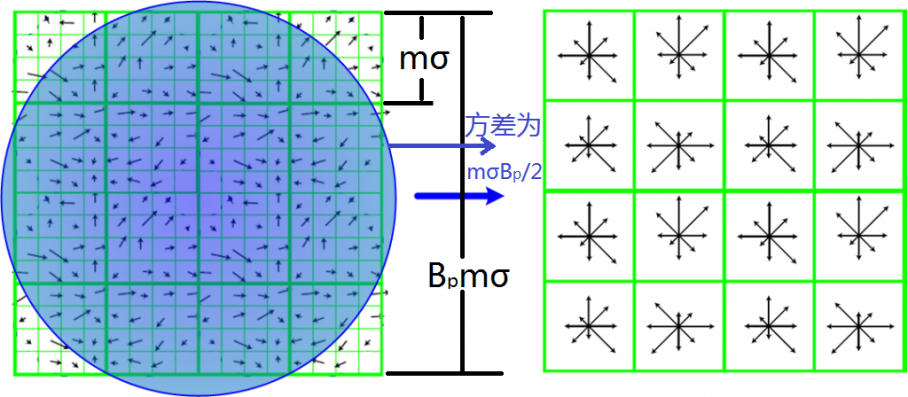
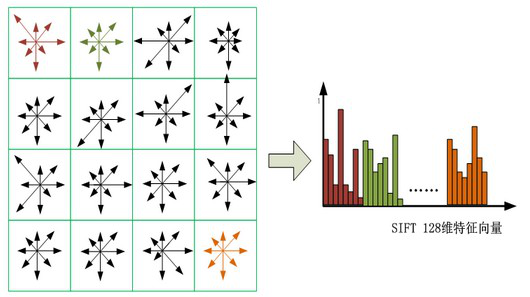
在每子區域內計算8個方向的梯度方向直方圖，繪制每個梯度方向的累加值，形成一個種子點。與求特征點主方向時有所不同，此時，每個子區域的梯度方向直方圖將0°~360°劃分為8個方向範圍，每個範圍為45°，這樣，每個種子點共有8個方向的梯度強度信息。由於存在4X4（Bp X Bp）個子區域，所以，共有4X4X8=128個數據，最終形成128維的SIFT特征矢量。同樣，對於特征矢量需要進行高斯加權處理，加權采用方差為mσBp/2的標準高斯函數，其中距離為各點相對於特征點的距離。使用高斯權重的是為了防止位置微小的變化給特征向量帶來很大的改變，並且給遠離特征點的點賦予較小的權重，以防止錯誤的匹配。

在最後，對特征向量進行歸一化處理，去除光照變化的影響。

8.使用特征檢測器

Opencv提供FeatureDetector實現特征點檢測。

最後把所檢測到的特征點放置在一個容器中，再進行後續的圖像匹配工作。

至此，SIFT特征匹配算法講解結束。

https://www.leiphone.com/news/201708/ZKsGd2JRKr766wEd.html關於HOG特征的解釋

SIFT特征匹配算法介紹