【題目描述】

給出一個有向圖G=(V, E)，和一個源點v0∈V，請寫一個程序輸出v0和圖G中其它頂點的最短路徑。只要所有的有向環權值和都是正的，我們就允許圖的邊有負值。頂點的標號從1到n（n為圖G的頂點數）。

【輸入】

第1行：一個正數n（2≤n≤80），表示圖G的頂點總數。

第2行：一個整數，表示源點v0（v0∈V，v0可以是圖G中任意一個頂點）。

第3至第n+2行，用一個鄰接矩陣W給出了這個圖。

【輸出】

共包含n-1行，按照頂點編號從小到大的順序，每行輸出源點v0到一個頂點的最短距離。每行的具體格式參照樣例。

【輸入樣例】

5
1
0 2 - - 10
- 0 3 - 7
- - 0 4 -
- - - 0 5
- - 6 - 0

【輸出樣例】

(1 -> 2) = 2
(1 -> 3) = 5
(1 -> 4) = 9
(1 -> 5) = 9

【提示】

樣例所對應的圖如下:

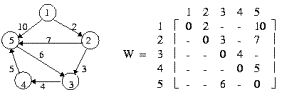
嗯～一個簡單的Floyed應用題，正好練練手

Floyd算法

1.定義概覽

Floyd-Warshall算法（Floyd-Warshall algorithm）是解決任意兩點間的最短路徑的一種算法，可以正確處理有向圖或負權的最短路徑問題，同時也被用於計算有向圖的傳遞閉包。Floyd-Warshall算法的時間復雜度為O(N³)，空間復雜度為O(N²)。

2.算法描述

算法思想原理：

Floyd算法是一個經典的動態規劃算法。用通俗的語言來描述的話，首先我們的目標是尋找從點i到點j的最短路徑。從動態規劃的角度看問題，我們需要為這個目標重新做一個詮釋（這個詮釋正是動態規劃最富創造力的精華所在）

從任意節點i到任意節點j的最短路徑不外乎2種可能，1是直接從i到j，2是從i經過若幹個節點k到j。所以，我們假設Dis(i,j)為節點u到節點v的最短路徑的距離，對於每一個節點k，我們檢查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，證明從i到k再到j的路徑比i直接到j的路徑短，我們便設置Dis(i,j) = Dis(i,k) + Dis(k,j)，這樣一來，當我們遍歷完所有節點k，Dis(i,j)中記錄的便是i到j的最短路徑的距離。

我們可以開一個n*n的鄰接矩陣，記錄聯通情況：f[i][j]如果為1，則說明i到j聯通；如果為∞，則說明不連通（之所以用∞的原因是比較的時候無窮大一定比任何除無窮大以外的數的和都大，這樣就不會把∞算進去），然後可以進一步將f[i][j]=1的地方利用兩點間距離公式將1換成具體的距離

簡單說一下思路：

根據題目給出的鄰接矩陣，利用Floyd算法求出各個點間的最短路徑，然後挨個輸出所求點到每個點的最短路徑，代碼如下：

#include<iostream>
#include<cstdio>
using namespace std;
int n,x,a[100][100];                           //a數組存放鄰接矩陣 
int ch;
const int maxn=0x3f3f3f3f;                     //給定一個很大的數，表示兩點間不連通 
int main()
{
    cin>>n>>x;
    for(int i=1;i<=n;i++)
       for(int j=1;j<=n;j++)
       {
           if(scanf("%d",&ch)) a[i][j]=ch;       //如果輸入合法，則賦值給a[i][j]，0也包含 
           else a[i][j]=maxn;                    //如果不合法，說明不連通，賦值maxn 
       }
    for(int k=1;k<=n;k++)                     //Floyd算法 
       for(int i=1;i<=n;i++)
          for(int j=1;j<=n;j++)
             if(i!=j&&j!=k&&k!=i&&(a[i][j]>a[i][k]+a[k][j]))
                a[i][j]=a[i][k]+a[k][j];      //更新最短路 
    for(int i=1;i<=n;i++)
    {
        if(i!=x)
        {
            cout<<"("<<x<<" -> "<<i<<") = "<<a[x][i]<<endl;     //輸出到其他點的最短路 
        }
    }
    return 0;
}

一本通網站 1378：最短路徑(shopth)