如果有1個數組，陣列的左半部分和右半部分都已經排好序，如何將該數組合成1個有序的陣列？

開闢1個同樣大小的臨時空間輔助我們完成歸併過程，如下圖

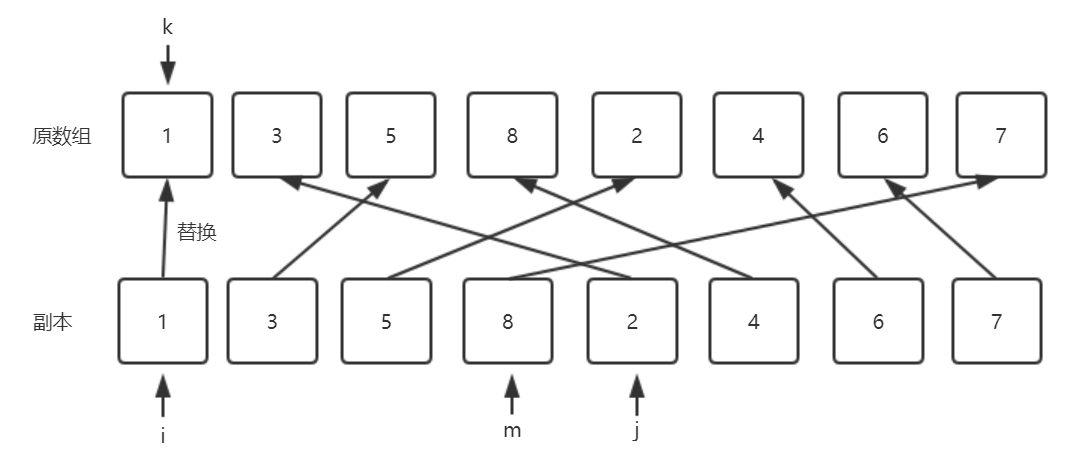
k:表示歸併過程中，當前需要替換的原陣列位置

i，j：要替換k位置的資料，當前需要考慮的元素，也就是從i和j位置中的元素中取1個最小的，替換到原陣列k的位置。

m：中間位置，也就是陣列左半部分最大的索引位置。

第一次：i和j位置的元素比較，1比2小，則將1替換k的位置，然後i++，k++；

第二次：i和j位置的元素比較，3比2大, 則將2替換k的位置，然後j++，k++；

依次類推,最後原陣列就變成了1個有序的陣列，這就是歸併的過程。

程式碼實現：

    /**
     * 合併函式
     * @param arr   原始陣列
     * @param left  要合併陣列的最左側索引位置
     * @param mid   左側有序陣列和右側有序陣列的分界線
     * @param right 要合併陣列的最右側索引位置
     */
    void __merge(int[] arr, int left, int mid, int right) {
        //將arr陣列 left~right之間的元素copy到arrCopy中
        int[] arrCopy = new int[right - left + 1];
        for (int i = left; i <= right; i++)
            arrCopy[i - left] = arr[i];//賦值

        int i = left, j = mid + 1;
        //給arr陣列left ~ right之間的陣列賦值
        for (int k = left; k <= right; k++) {
            if (i > mid) {//如果i大於mid,說明左側已沒有可以賦值的元素，則選取右側的元素
                arr[k] = arrCopy[j - left];
                j++;
            } else if (j > right) {//說明右側已沒有賦值的元素，則選取左側的元素
                arr[k] = arrCopy[i - left];
                i++;
            } else if (arrCopy[i - left] < arrCopy[j - left]) {//左側元素小於右側元素，選取左側元素
                arr[k] = arrCopy[i - left];
                i++;
            } else {//否則選取右側元素
                arr[k] = arrCopy[j - left];
                j++;
            }
        }
    }
 

測試：

    @Test
    public void test__merge(){
        int[] arr = new int[]{1,3,5,8,2,4,6,7};
        int left = 0;
        int right = arr.length - 1;
        int mid = (left + right)/2;
        __merge(arr,left,mid,right);
        Arrays.stream(arr).forEach(item->{
            System.out.print(item + " ");
        });
    }
 

測試結果如下，從測試結果可以看出，陣列已經變成一個有序的陣列。

如果我們要對陣列 5,1,3,8,7,4,6,2 進行排序，可以將其分為兩個大小各為4的子陣列，對兩個子陣列進行排序，然後合併它們，生成有序陣列。同樣，可以將每個子陣列，再次劃分成兩個子陣列，然後對子陣列進行排序和合並。依次劃分，直到子陣列大小變為1。 這樣就可以將一個無序的陣列變成有序的陣列。

程式碼實現：

    /**
     *遞迴使用歸併排序,對arr[left....right]範圍進行排序
     * @param arr
     * @param left
     * @param right
     */
    public void mergeSort(int[] arr,int left,int right){
        if (left >= right)//如果只有1個元素，返回
            return;
        int mid = (left + right)/2;
        mergeSort(arr,left,mid);//整個函式執行完,arr[left....mid]變成有序
        mergeSort(arr,mid + 1,right);//arr[mid + 1....right]變成有序
        __merge(arr,left,mid,right);//合併後，arr[left....right] 變成有序。
    }

測試

    @Test
    public void test__mergeSort(){
        int[] arr = new int[]{5,1,3,8,7,4,6,2};
        int left = 0;
        int right = arr.length-1;
        mergeSort(arr,left,right);
        Arrays.stream(arr).forEach(item->{
            System.out.print(item + " ");
        });
    }

從執行結果可以看出陣列已經排好序。

時間複雜度分析

我們假設對n個元素進行歸併排序需要的時間為T(n),那麼分解成兩個子陣列排序的時間都是T(n/2),__merge合併兩個子陣列的時間複雜度為O(n)，則歸併排序的時間複雜度公式如下：

T(1) = C；   n=1 時，只需要常量級的執行時間，所以表示為 C。
T(n) = 2*T(n/2) + n； n>1

通過這個公式，進行分解：

T(n) = 2*T(n/2) + n
     = 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
     = 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
     = 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
     ......
     = 2^k * T(n/2^k) + k * n
     ......

當 T(n/2^k)=T(1) 時，也就是 n/2^k=1，可以得到k=log2n，所以T(n) = nlog2n+Cn。用大O表示法的話，其時間複雜度為O(nlogn).

歸併排序的執行效率與原始陣列的有序程度無關，所以是非常穩定的排序演算法，最好、最壞、平均 時間複雜度都是O(nlogn)。