【動態規劃】多重背包問題
說明
前面已經介紹完了01背包和完全背包,今天介紹最後一種背包問題——多重背包。
這個背包,聽起來就很麻煩的樣子。別慌,只要你理解了前面的兩種背包問題,拿下多重背包簡直小菜一碟。
如果沒有看過前兩篇01背包和完全背包的文章,強烈建議先閱讀一下,因為本文跟前兩篇文章關聯性很強。
多重背包
有N種物品和一個容量為T的背包,第i種物品最多有M[i]件可用,價值為P[i],體積為V[i],求解:選哪些物品放入背包,可以使得這些物品的價值最大,並且體積總和不超過背包容量。
對比一下完全背包,其實只是多了一個限制條件,完全背包問題中,物品可以選擇任意多件,只要你裝得下,裝多少件都行。

但多重背包就不一樣了,每種物品都有指定的數量限制,所以不是你想裝,就能一直裝的。
舉個栗子:有A、B、C三種物品,相應的數量、價格和占用空間如下圖:
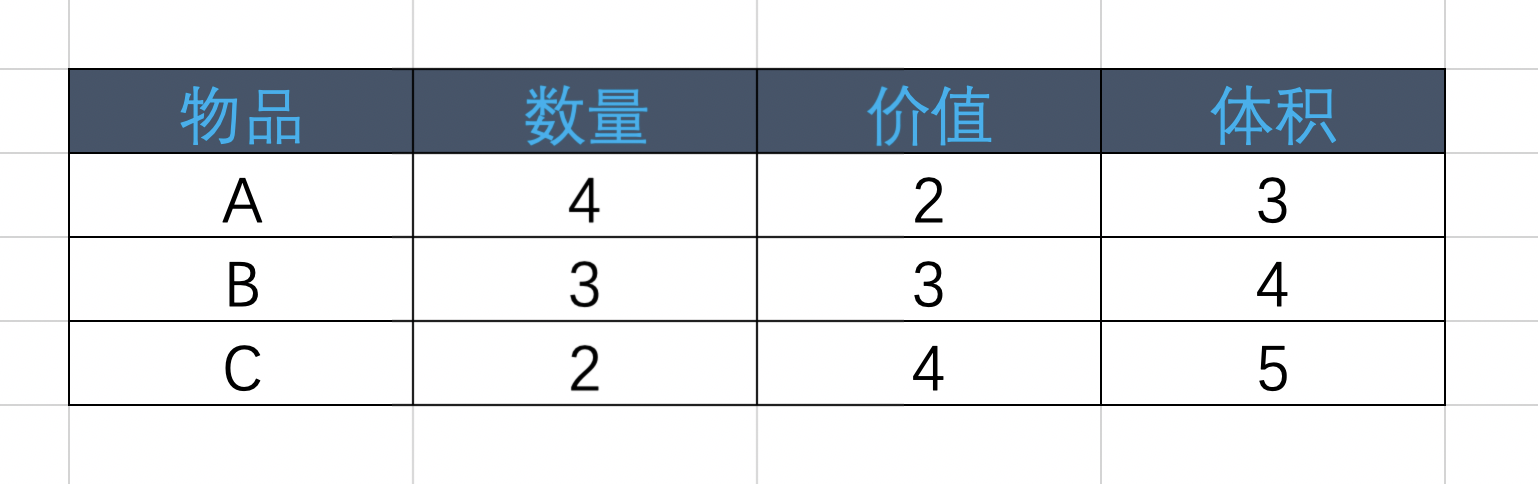
跟完全背包一樣,貪心算法在這裏也不適用,我就不重復說明了,大家可以回到上一篇中看看說明。
遞歸法
還是用之前的套路,我們先來用遞歸把這個問題解決一次。
用ks(i,t)表示前i種物品放入一個容量為t的背包獲得的最大價值,那麽對於第i種物品,我們有k種選擇,0 <= k <= M[i] && 0 <= k * V[i] <= t,即可以選擇0、1、2...M[i]個第i種物品,所以遞推表達式為:
ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k <= M[i] && 0 <= k * V[i] <= t)
同時,ks(0,t)=0;ks(i,0)=0;
對比一下完全背包的遞推關系式:
ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k * V[i] <= t)簡直一毛一樣,只是k多了一個限制條件而已。
使用上面的栗子,我們可以先寫出遞歸解法:
public static class MultiKnapsack { private static int[] P={0,2,3,4}; private static int[] V={0,3,4,5}; private static int[] M={0,4,3,2}; private static int T = 15; @Test public void soleve1() { int result = ks(P.length - 1,T); System.out.println("最大價值為:" + result); } private int ks(int i, int t){ int result = 0; if (i == 0 || t == 0){ // 初始條件 result = 0; } else if(V[i] > t){ // 裝不下該珠寶 result = ks(i-1, t); } else { // 可以裝下 // 取k個物品i,取其中使得總價值最大的k for (int k = 0; k <= M[i] && k * V[i] <= t; k++){ int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k; if (tmp2 > result){ result = tmp2; } } } return result; } }
同樣,這裏的數組P/V/M分別添加了一個元素0,是為了減少越界判斷而做的簡單處理,運行如下:
最大價值為:11對比一下完全背包中的遞歸解法:
private int ks(int i, int t){
int result = 0;
if (i == 0 || t == 0){
// 初始條件
result = 0;
} else if(V[i] > t){
// 裝不下該珠寶
result = ks(i-1, t);
} else {
// 可以裝下
// 取k個物品i,取其中使得總價值最大的k
for (int k = 0; k * V[i] <= t; k++){
int tmp2 = ks(i-1, t - V[i] * k) + P[i] * k;
if (tmp2 > result){
result = tmp2;
}
}
}
return result;
}僅僅多了一個判斷條件而已,所以只要弄懂了完全背包,多重背包就不值一提了。
最優化原理和無後效性的證明跟多重背包基本一致,所以就不重復證明了。
動態規劃
參考完全背包的動態規劃解法,就很容易寫出多重背包的動態規劃解法。
自上而下記憶法
ks(i,t) = max{ks(i-1, t - V[i] * k) + P[i] * k}; (0 <= k <= M[i] && 0 <= k * V[i] <= t)public static class MultiKnapsack {
private static int[] P={0,2,3,4};
private static int[] V={0,3,4,5};
private static int[] M={0,4,3,2};
private static int T = 15;
private Integer[][] results = new Integer[P.length + 1][T + 1];
@Test
public void solve2() {
int result = ks2(P.length - 1,T);
System.out.println("最大價值為:" + result);
}
private int ks2(int i, int t){
// 如果該結果已經被計算,那麽直接返回
if (results[i][t] != null) return results[i][t];
int result = 0;
if (i == 0 || t == 0){
// 初始條件
result = 0;
} else if(V[i] > t){
// 裝不下該珠寶
result = ks2(i-1, t);
} else {
// 可以裝下
// 取k個物品,取其中使得價值最大的
for (int k = 0; k <= M[i] && k * V[i] <= t; k++){
int tmp2 = ks2(i-1, t - V[i] * k) + P[i] * k;
if (tmp2 > result){
result = tmp2;
}
}
}
results[i][t] = result;
return result;
}
}這裏其實只是照葫蘆畫瓢。
自下而上填表法
同樣也可以使用填表法來解決,此時需要將數組P、V、M額外添加的元素0去掉。
除了k的限制不一樣之外,其他地方跟完全背包的解法完全一致:
public static class MultiKnapsack {
private static int[] P={2,3,4};
private static int[] V={3,4,5};
private static int[] M={4,3,2};
private static int T = 15;
private int[][] dp = new int[P.length + 1][T + 1];
@Test
public void solve3() {
for (int i = 0; i < P.length; i++){
for (int j = 0; j <= T; j++){
for (int k = 0; k <= M[i] && k * V[i] <= j; k++){
dp[i+1][j] = Math.max(dp[i+1][j], dp[i][j-k * V[i]] + k * P[i]);
}
}
}
System.out.println("最大價值為:" + dp[P.length][T]);
}
}跟01背包問題一樣,完全背包的空間復雜度也可以進行優化,具體思路這裏就不重復介紹了,可以翻看前面的01背包問題優化篇。
優化後的狀態轉移方程為:
ks(t) = max{ks(t), ks(t - Vi) + Pi}public static class MultiKnapsack {
private static int[] P={2,3,4};
private static int[] V={3,4,5};
private static int[] M={4,3,2};
private static int T = 15;
private int[] newResults = new int[T + 1];
@Test
public void resolve4() {
int result = ksp(P.length,T);
System.out.println(result);
}
private int ksp(int i, int t){
// 開始填表
for (int m = 0; m < i; m++){
for (int n = V[m]; n <= t ; n++){
if (n >= V[m] * (M[m] + 1)){
newResults[n] = newResults[n - 1];
}else {
newResults[n] = Math.max(newResults[n] , newResults[n - V[m]] + P[m]);
}
}
// 可以在這裏輸出中間結果
System.out.println(JSON.toJSONString(newResults));
}
return newResults[newResults.length - 1];
}
}輸出如下:
[0,0,0,2,2,2,4,4,4,6,6,6,8,8,8,8]
[0,0,0,2,3,3,4,5,6,6,7,8,9,9,10,11]
[0,0,0,2,3,4,4,5,6,7,8,8,9,10,11,11]
11這裏的優化多了一個限制條件,跟完全背包相比,唯一的區別在這裏:
if (n >= V[m] * (M[m] + 1)){
newResults[n] = newResults[n - 1];
}else {
newResults[n] = Math.max(newResults[n] , newResults[n - V[m]] + P[m]);
}代碼很簡單,但要理解卻並不容易,為了加深理解,再畫一張圖:
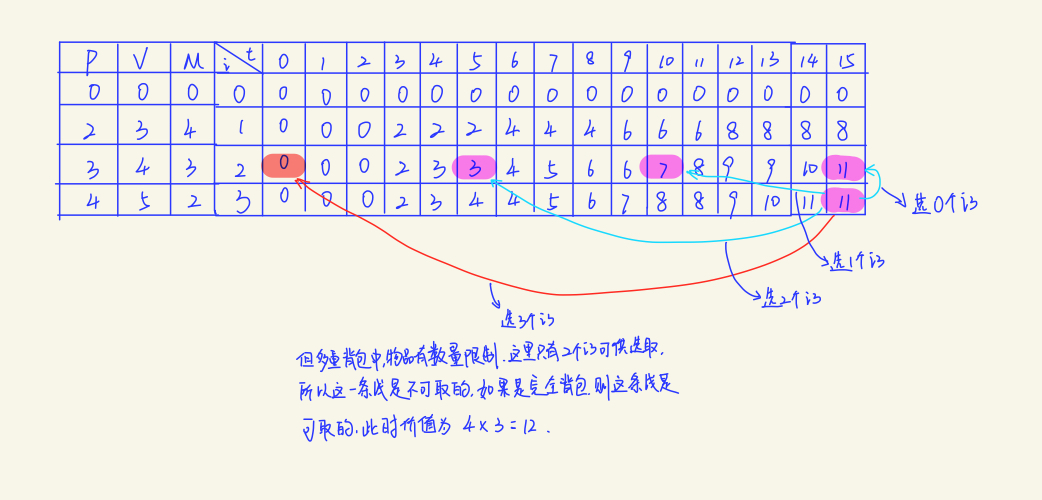
多重背包問題同樣也可以轉化成01背包問題來求解,因為第i件物品最多選 M[i] 件,於是可以把第i種物品轉化為M[i]件體積和價值相同的物品,然後再來求解這個01背包問題。
總結
多重背包問題跟完全背包簡直如出一轍,僅僅是比完全背包多一個限制條件而已,如果你回過頭去看看前一篇文章,就會發現這篇文章簡直就是抄襲。。

關於多重背包問題的解析到此就結束了,三個經典的背包問題到這裏就告一段落了。

如果有疑問或者有什麽想法,也歡迎關註我的公眾號進行留言交流:

【動態規劃】多重背包問題
