【等距螺旋的別名是等速度比螺旋】

等距螺旋的公式中，直線速度w與圓周速度v並不獨立出現，而是以速度比的形式出現，如下所示：

• 等距螺旋中存在突變點，突變點對應的角度為-v/(w*CosDA)。

（註：由於v與w均為正值，DA角範圍為（-90°，90°）因此，突變點僅出現在負值區間。由於螺旋的對稱效應，可使用-α來代表與α方向相反的螺旋，計算時按α>0來分析。）

• 從圓周移動到近地點，共需要經歷的旋轉角度為v*cosDA/w（弧度單位）。

通過以上的這些計算都可以看到，直線速度與基圓速度的比值可以用來判斷螺旋是否是等距離外擴（比值恒定為等距螺旋，不恒定為非等距螺旋），或者螺旋是否相同（不同的速度搭配，若速度比值相同即為同一條螺旋）。

當旋轉速度加倍，直線速度同時也加倍的情況下，速度的比值沒有發生變化，即螺旋的公式將不會發生變化，也就是說速度同時加倍的情況下，仍屬於同一條螺旋。漸開線打開的快慢，並不影響它的螺旋軌跡的大小，就是這一原理的最佳證據。

再回到阿基米德螺旋的一個經典案例，小蟲勻速從唱片的中心向外爬去。小蟲越向外走，我們觀察到的小蟲的弧線速度是在增加的，但它所形成的螺旋軌跡卻是等距離外擴的。在這裏，小蟲的直線速度對應的基圓速度（阿基米德螺旋並未提到基圓的概念，但它是真實存在的）之比是固定的，因此，它屬於等距離外擴的螺旋。小蟲的直線運動穿過圓心，因此，螺旋軌跡屬於等距螺旋中的阿基米德螺旋。

在小蟲與唱片這樣的旋轉系統中，小蟲與唱片之間存在摩擦力，這種摩擦力使得小蟲的弧線速度在不斷的增加，當小蟲從唱片外沿掉落的時候，它的速度相當於唱片外沿的速度與直線爬行速度的疊加。小蟲的直線爬行速度與基圓速度相綁定，與它實際的空間速度無關。唱片每一個旋轉周期的時間是固定的，傳統的分析中引入了角動量的概念，而角動量可以線性的轉化為基圓速度v，從速度比的角度來看，它們的速度比是一個固定值，因此屬於等距螺旋。

【非等距螺旋的聯想】

（直線運動與圓周運動的）速度比恒定的情況下會產生等距離外擴螺旋，那麽速度比均勻增加或均勻減小的情況下，必然出現加速度外擴（或是收縮）的螺旋，它些螺旋可以統稱為非等距螺旋

非等距螺旋是自然界中更為常見的螺旋形式。非等距螺旋中的速度比變化，可以看作是圓周旋轉速度的加速，或是直線運動的加速。為了簡化分析起見，通常可以認為圓周一直是勻速運動的，而直線運動存在加速和減速兩種狀態。

如果我們的宇宙處於某個非等距螺旋軌道上，周圍的星體也同樣位於這樣的軌道中。那麽，當這個旋轉系統的旋轉速度在減慢，而直線速度並未變化的情況下，從我們觀察的角度來看，會發現世界在加速膨脹。因為，我們進入了螺旋的發散階段，各個星體軌跡之間的微小差異，都會在不斷的放大。從這樣的角度來看，宇宙的膨脹並不需要外力來支持，而只是我們所處的世界旋轉的更慢了一些而已。

前面兩張圖形實際上是數學公式出錯的產物，非等距螺旋的分析是等距螺旋理論的進一步延伸，我們只是站在它的門口向裏面望了一眼而已。古人雲“吾生也有涯，而知也無涯。以有涯隨無涯，殆已”，所以這個方向的討論留給對數學感興趣的朋友們繼續吧。

【為什麽會有突變點】

在等距螺旋的公式裏，角度進入到負值區間的某個位置時，會出現突變，螺旋軌跡會進入到它的互補螺旋的軌跡中去。那麽，為什麽會有突變點呢？

首先，這是數學公式的不完美造成的。當我們試圖用單一公式來表達順時針外擴與逆時針外擴的螺旋時，就會發現在某個位置，公式出現了“錯誤”。所以對於數學公式應保持警惕的態度，在沒有對參數區間進行完整論證之前，不要先入為主的以為數據是平滑安全的。

其次，這是由於螺旋的互補性造成的。在螺旋的世界裏順時針旋轉的螺旋與逆時針旋轉的螺旋互補，它們在角度關系與表達式上是非常近似的。二者角度之間相差180度，突變點的計算過程也正好符合這樣的一種設定。

從科幻的角度來說，電影、小說裏對於時空穿越點的描述已經是常態化的標配了，突變點的存在非常默契的配合了這樣的題材。盡管我個人對時空穿越持懷疑態度（少部分人的穿越，讓全世界來陪同，這個能量消耗不科學啊），但如果這樣能幫助我們更好的理解突變點，倒也不妨按這個思路去想象一下。

【等距螺旋的過去、現在和未來】

阿基米德（公元前287年—公元前212年）在距今兩千兩百多年前將“螺線”定義為一個勻速運動的點沿直線從圓心向外運動，直線同時進行勻速旋轉時，動點所形成的螺旋狀曲線。由於最初的這種定義，很多人以為只有勻速運動才能得到螺旋，故又將它稱為等速螺旋。

網上搜索漸開線起源，幾乎全部與齒輪相關，真實的出現年代反而無從考證。齒輪最早在公元前400年至200年出現在中國，1694年法國科學家Philippe首先提出漸開線可作為齒形曲線，此後漸開線在齒輪加工領域裏得到了逐步的發展。新中國成立之初，我們幾乎沒有現化化齒輪的加工能力，經過很多人的努力，最終形成了完整的加工體系。

風螺旋（wind spiral）是隨著航空工業的發展而引入的一種螺旋，在上個世紀開始的國際民航組織8168文件中，對風螺旋進行了描述，它假想航空器在轉彎過程中，受到累積風的影響而形成的螺旋狀的最大外邊界。國際民航組織並未對風螺旋給出相應的計算公式，這使得飛行程序保護區在自動化繪制時遇到了非常大的困難。不少人使用阿基米德螺旋來代替風螺旋，除了極易產生範圍偏小或者精度不夠的情況外，等距外擴、切線與公切線的計算都走入了死胡通。

2014年8月，《風螺旋線的深度分析》一文在《空中交通》雜誌正式刊發，文中列出的風螺旋公式就是後來的等距螺旋公式1與公式2。此後，相繼完成了傳統程序保護區的算法分析，論文選題覆蓋了程序轉彎（2017年）、基線轉彎（2017年）、等待程序（2018年）。算法中解決了切線與公切線的計算，並且非常簡單的實現了等距外擴的計算。

在傳統程序保護區分析論證的基礎之上，通過對風螺旋的算法進行全面的回顧整理，對照其它的典型螺旋進行分析，最終發現風螺旋公式在特定角度條件下，可以成功的轉換為阿基米德公式以及漸開線公式，從運動形式到計算方法，實現了螺旋概念的統一。2018年6月《數學的實踐與認識》刊發了《等距螺旋的原理與計算》，標誌著全新的螺旋概念的形成。文章中對典型螺旋的公式轉換方法進行了詳細的分析，證明了風螺旋並不是一個孤立的存在，而是等距螺旋的通用公式。

2019年，風螺旋在PBN中的算法應用文章將陸續刊發，實現從傳統程序向PBN保護區算法的跨越。未來隨著PBN技術的廣泛應用，風螺旋算法在飛行程序中必將取得更廣闊的發展空間。

【等距螺旋的特性】

當我們觀察一條“完整”的等距螺旋時，我們首先會發現它是軸對稱圖形，也就是說完整的螺旋具備對稱性。

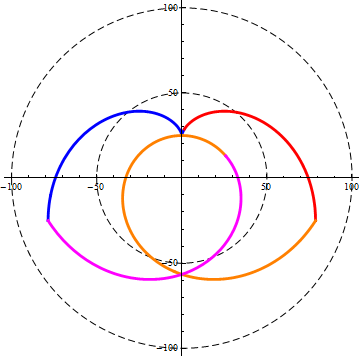
其次，正向旋轉與反向旋轉，會得到兩條互補的螺旋，它們會在近地點的位置相切，這是螺旋所體現出的互補性。互補的兩條螺旋在公式表達上，也體出了互換的特點，當螺旋經過突變點時，正向螺旋的公式會與反向螺旋的公式互換，並且按照交換後的公式繼續發展。

基礎參數相同的等距螺旋，無論它們出發時的角度有多麽不同，經過多個周期的旋轉外擴之後，它們看起來都會非常的相似，這體現了等距螺旋的趨同性。

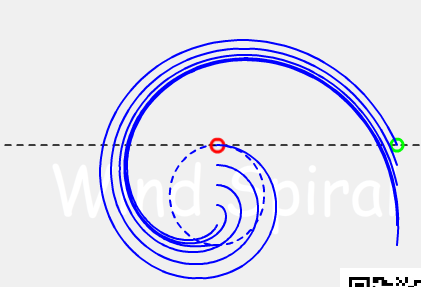
【等距螺旋的哲學意義】

我們的世界中隨處可見螺旋的影子，讓人不禁猜想，大的宇宙體系是否也是某種螺旋擴散的結構。

從完整的螺旋運動軌跡來看，世界可以從無限遠處逐漸旋轉收縮，到達最接近圓心的位置（近地點）後，再繼續旋轉放大，去向無限遠的地方。這種不知道起點、終點的狀況，用“無所從來，無所從往”來描述最恰當不過。雖然不知道起點、終點，但從螺旋的軌跡上可以確定的是，我們從哪裏來，必將回到哪裏去。

我們已知宇宙進入了膨脹的周期，這意味著經過了收縮周期（如果有的話）之後，我們已經是在“回去”的路上了。剩下的唯一問題就是時間，宇宙僅僅是膨脹以來的時間就有大約150億年，如果“來時”用了相同的時間，那麽回去也該差不多的時間才可以。在這個漫長而孤獨的星際旅行裏，照顧好自己，照顧好身邊的人，照顧好我們的星球就是最基本的生命意義。

回到個體的角度來看，在運動方式固定的情況下，所有的螺旋最終都是相似的。這意味沒有所謂的捷徑，堅持各自的方向就是最佳的選擇，“萬千法門皆可得道”說的就是這種情形。正如大多數人的生活一樣，走過的路或許不同，但生命的軌跡卻一定是相似的。

感謝您閱讀至此，今天的文字超長，是因為在終結這個系列的話題之前，想說的話還有太多。今天的很多內容已經是未經實驗，僅供猜想的成分了。簡單來說，等距螺旋的研究還有很多方向，但時間和精力的關系，只能先止步於此了。後續我們將集中精力，回到飛行程序算法分析的軌道上去，力爭在風螺旋算法的推廣之路上走得更遠，飛得更高。

【等距螺旋的七個實驗】實驗七：等距螺旋的別名是等速度比螺旋