樹的基本術語

• 結點（node）由資料元素以及指向子樹的地址構成。
• 若 X 結點有子樹，則子樹的根結點稱為 X 的孩子（child）結點，相應地，
  X 稱為其孩子的雙親（parents）結點，又稱父母結點。
• 同一雙親的孩子結點之間互稱兄弟（sibling）結點。
• 葉子（leaf）結點是指度為 0 的結點，又稱為終端結點。其他的叫分支結點

二叉樹的定義

二叉樹由一個根結點或兩棵互不相交的、分別稱為左子樹和右子樹的子二叉樹構成。

二叉樹的性質

• 二叉樹的結點最多隻有兩棵子樹
• 若根結點的層次為 1，則二叉樹第 i 層的結點數目最多為 2^i-1（i≥1）個。
• 在深度為 k 的二叉樹中，至多有 2^k -1 個結點（k≥0）。

• 二叉樹中，若葉子結點數為 n0，度為 2 的結點數為 n2，則有 n0=n2+1。

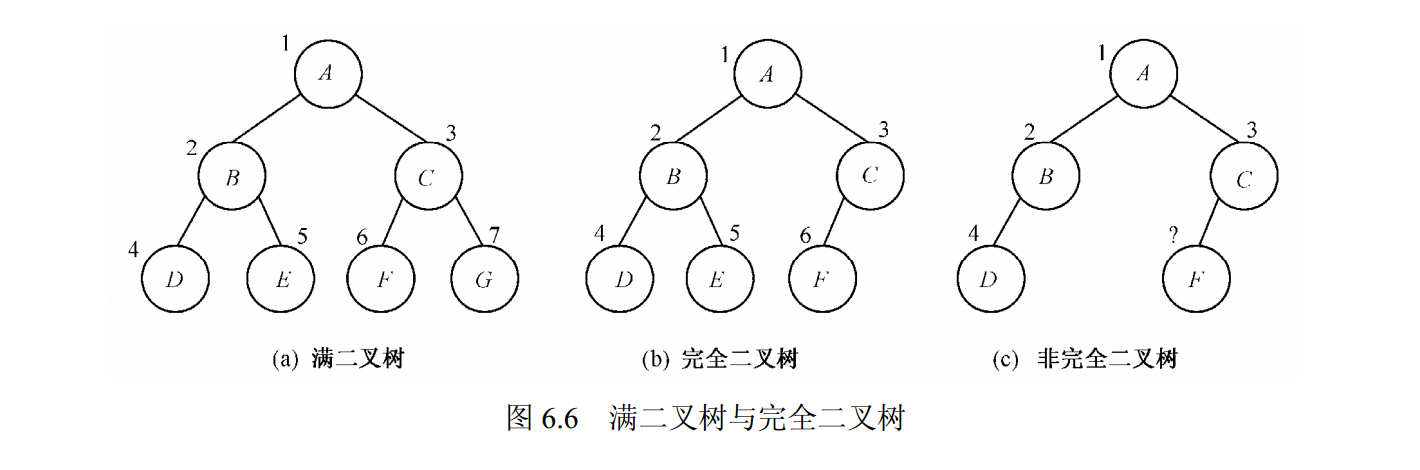
• 滿二叉樹:一棵深度為 k 的滿二叉樹（full binary tree）是具有 2^k -1 （k≥0）個結點的二叉樹。滿二叉樹每一層的結點數目都達到最大值.

• 完全二叉樹:一棵具有 n 個結點深度為 k 的二叉樹，如果它的每一個結點都與深度為 k 的滿二叉樹中編
  號為 1～n 的結點一一對應，則稱這棵二叉樹為完全二叉樹（complete binary tree）

二叉樹的儲存結構

二叉樹的儲存結構有兩種：順序儲存結構和鏈式儲存結構。

順序儲存

二叉樹的順序儲存結構適用於完全二叉樹，對完全二叉樹進行順序編號，將編號為 i 的結

鏈式儲存

一般情況下，採用鏈式儲存結構來儲存二叉樹。每個結點有 3 個域：

• data 表示結點的資料元素。
• left 指向該結點的左孩子結點，即左子樹的根結點。
• right 指向該結點的右孩子結點，即右子樹的根結點。

二叉樹的遍歷

先根序遍歷(DLR)

訪問根結點，遍歷左子樹，遍歷右子樹。表示式的字首表示（波蘭式）

中根序遍歷(LDR)

遍歷左子樹，訪問根結點，遍歷右子樹。表示式的中綴表示

後根序遍歷(LRD)

遍歷左子樹，遍歷右子樹，訪問根結點。表示式的字尾表示（逆波蘭式