2. 程式人生 > >Java動態規劃

Java動態規劃

阿新 • • 發佈：2019-06-27

1. 介紹

動態規劃典型的被用於優化遞迴演算法，因為它們傾向於以指數的方式進行擴充套件。動態規劃主要思想是將複雜問題（帶有許多遞迴呼叫）分解為更小的子問題，然後將它們儲存到記憶體中，這樣我們就不必在每次使用它們時重新計算它們。

要理解動態規劃的概念，我們需要熟悉一些主題：

  1. 什麼是動態規劃？
  2. 貪心演算法
  3. 簡化的揹包問題
  4. 傳統的揹包問題
  5. Levenshtein Distance
  6. LCS-最長的共同子序列
  7. 利用動態規劃的其他問題
  8. 結論

本文所有程式碼均為java程式碼實現。

2. 什麼是動態規劃？

動態規劃是一種程式設計原理，可以通過將非常複雜的問題劃分為更小的子問題來解決。這個原則與遞迴很類似，但是與遞迴有一個關鍵點的不同，就是每個不同的子問題只能被解決一次。

為了理解動態規劃，我們首先需要理解遞迴關係的問題。每個單獨的複雜問題可以被劃分為很小的子問題，這表示我們可以在這些問題之間構造一個遞迴關係。
讓我們來看一個我們所熟悉的例子：斐波拉契數列，斐波拉契數列的定義具有以下的遞迴關係：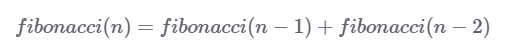

注意：遞迴關係是遞迴地定義下一項是先前項的函式的序列的等式。Fibonacci序列就是一個很好的例子。

所以，如果我們想要找到斐波拉契數列序列中的第n個數，我們必須知道序列中第n個前面的兩個數字。

但是，每次我們想要計算Fibonacci序列的不同元素時，我們在遞迴呼叫中都有一些重複呼叫，如下圖所示，我們計算Fibonacci（5）

：

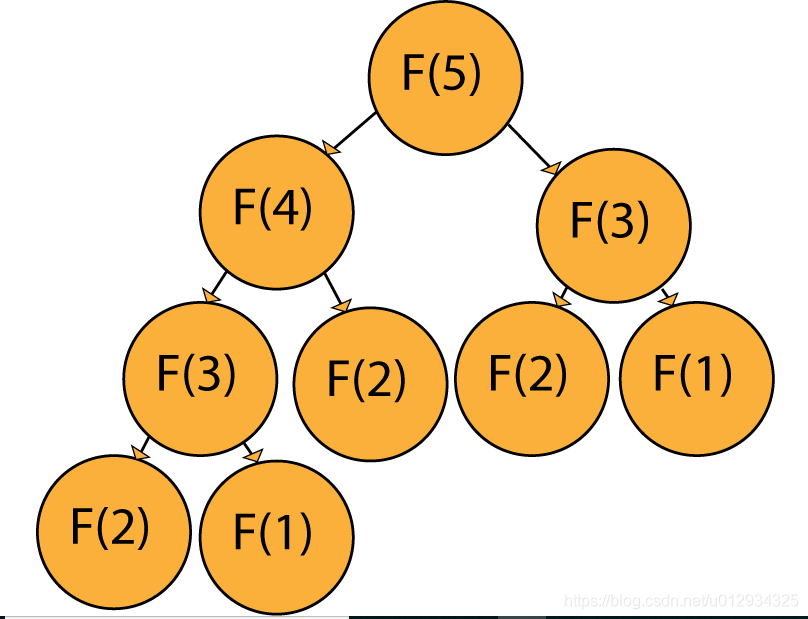
例如：如果我們想計算F(5),明顯的我們需要計算F(3)和F(4)作為計算F(5)的先決條件。然而，為了計算F(4)，我們需要計算F(3)和F(2)，因此我們又需要計算F(2)和F(1)來得到F(3)，其他的求解諸如此類。

這樣的話就會導致很多重複的計算，這些重複計算本質上是冗餘的，並且明顯的減慢了演算法的效率。為了解決這種問題，我們介紹動態規劃。

在這種方法中，我們對解決方案進行建模，就像我們要遞迴地解決它一樣，但我們從頭開始解決它，記憶到達頂部採取的子問題（子步驟）的解決方案。
因此，對於Fibonacci序列，我們首先求解並記憶F（1）和F（2）

，然後使用兩個記憶步驟計算F（3），依此類推。這意味著序列中每個單獨元素的計算都是O（1），因為我們已經知道前兩個元素。

當使用動態規劃解決問題的時候，我們一般會採用下面三個步驟：

  1. 確定適用於所述問題的遞迴關係
  2. 初始化記憶體、陣列、矩陣的初始值
  3. 確保當我們進行遞迴呼叫（可以訪問子問題的答案）的時候它總是被提前解決。

遵循這些規則，讓我們來看一下使用動態規劃的演算法的例子：

3. 貪心演算法

下面來以這個為例子：

Given a rod of length n and an array that contains prices of all pieces of size smaller than n. Determine the maximum value obtainable by cutting up the rod and selling the pieces.

3.1. 對於沒有經驗的開發者可能會採取下面這種做法

這個問題實際上是為動態規劃量身定做的，但是因為這是我們的第一個真例項子，讓我們看看執行這些程式碼會遇到多少問題：

public class naiveSolution {  
    static int getValue(int[] values, int length) {
        if (length <= 0)
            return 0;
        int tmpMax = -1;
        for (int i = 0; i < length; i++) {
            tmpMax = Math.max(tmpMax, values[i] + getValue(values, length - i - 1));
        }
        return tmpMax;
    }

    public static void main(String[] args) {
        int[] values = new int[]{3, 7, 1, 3, 9};
        int rodLength = values.length;

        System.out.println("Max rod value: " + getValue(values, rodLength));
    }
}

輸出結果：

Max rod value: 17

該解決方案雖然正確，但效率非常低，遞迴呼叫的結果沒有儲存，所以每次有重疊解決方案時，糟糕的程式碼不得不去解決相同的子問題。

3.2.動態方法

利用上面相同的基本原理，新增記憶化並排除遞迴呼叫，我們得到以下實現:

public class dpSolution {  
    static int getValue(int[] values, int rodLength) {
        int[] subSolutions = new int[rodLength + 1];

        for (int i = 1; i <= rodLength; i++) {
            int tmpMax = -1;
            for (int j = 0; j < i; j++)
                tmpMax = Math.max(tmpMax, values[j] + subSolutions[i - j - 1]);
            subSolutions[i] = tmpMax;
        }
        return subSolutions[rodLength];
    }

    public static void main(String[] args) {
        int[] values = new int[]{3, 7, 1, 3, 9};
        int rodLength = values.length;

        System.out.println("Max rod value: " + getValue(values, rodLength));
    }
}

輸出結果：

Max rod value: 17

正如我們所看到的的，輸出結果是一樣的，所不同的是時間和空間複雜度。

通過從頭開始解決子問題，我們消除了遞迴呼叫的需要，利用已解決給定問題的所有先前子問題的事實。

效能的提升

為了給出動態方法效率更高的觀點的證據，讓我們嘗試使用30個值來執行該演算法。 一種演算法需要大約5.2秒來執行，而動態解決方法需要大約0.000095秒來執行。

4. 簡化的揹包問題

簡化的揹包問題是一個優化問題，沒有一個解決方案。這個問題的問題是 - “解決方案是否存在？”：

Given a set of items, each with a weight w1, w2... determine the number of each item to put in a knapsack so that the total weight is less than or equal to a given limit K.

給定一組物品，每個物品的重量為w1，w2 …確定放入揹包中的每個物品的數量，以使總重量小於或等於給定的極限K

首先讓我們把元素的所有權重儲存在W陣列中。接下來，假設有n個專案，我們將使用從1到n的數字列舉它們，因此第i個專案的權重為W [i]。我們將形成（n + 1）x（K + 1）維的矩陣M。M [x] [y]對應於揹包問題的解決方案，但僅包括起始陣列的前x個項，並且最大容量為y

例如

假設我們有3個元素，權重分別是w1=2kg,w2=3kg,w3=4kg。利用上面的方法，我們可以說M [1] [2]是一個有效的解決方案。
這意味著我們正在嘗試用重量陣列中的第一個專案（w1）填充容量為2kg的揹包。

在M [3] [5]中，我們嘗試使用重量陣列的前3項（w1，w2，w3）填充容量為5kg的揹包。
這不是一個有效的解決方案，因為我們過度擬合它。

4.1. 矩陣初始化

當初始化矩陣的時候有兩點需要注意：

Does a solution exist for the given subproblem (M[x][y].exists) AND does the given solution include the latest item added to the array (M[x][y].includes).

給定子問題是否存在解（M [x] [y] .exists）並且給定解包括新增到陣列的最新項（M [x] [y] .includes）。

因此，初始化矩陣是相當容易的，M[0][k].exists總是false，如果k>0，因為我們沒有把任何物品放在帶有k容量的揹包裡。

另一方面，M[0][0].exists = true,當k=0的時候，揹包應該是空的，因此我們在裡面沒有放任何東西，這個是一個有效的解決方案。

此外，我們可以說M[k][0].exists = true，但是對於每個k來說 M[k][0].includes = false。

注意：僅僅因為對於給定的M [x] [y]存在解決方案，它並不一定意味著該特定組合是解決方案。
在M [10] [0]的情況下，存在一種解決方案 - 不包括10個元素中的任何一個。
這就是M [10] [0] .exists = true但M [10] [0] .includes = false的原因。

4.2.演算法原則

接下來，讓我們使用以下虛擬碼構造M [i] [k]的遞迴關係：

if (M[i-1][k].exists == True):  
    M[i][k].exists = True
    M[i][k].includes = False
elif (k-W[i]>=0):  
    if(M[i-1][k-W[i]].exists == true):
        M[i][k].exists = True
        M[i][k].includes = True
else:  
    M[i][k].exists = False

因此，解決方案的要點是將子問題分為兩種情況:

  1. 對於容量k,當存在第一個i-1元素的解決方案
  2. 對於容量k-W [i],當第一個i-1元素存在解決方案

第一種情況是不言自明的，我們已經有了問題的解決方案。

第二種情況是指了解第一個i-1元素的解決方案，但是容量只有一個第i個元素不滿，這意味著我們可以新增一個第i個元素，並且我們有一個新的解決方案！

4.3. 實現

下面這何種實現方式，使得事情變得更加容易，我們建立了一個類Element來儲存元素：

public class Element {  
    private boolean exists;
    private boolean includes;

    public Element(boolean exists, boolean includes) {
        this.exists = exists;
        this.includes = includes;
    }

    public Element(boolean exists) {
        this.exists = exists;
        this.includes = false;
    }

    public boolean isExists() {
        return exists;
    }

    public void setExists(boolean exists) {
        this.exists = exists;
    }

    public boolean isIncludes() {
        return includes;
    }

    public void setIncludes(boolean includes) {
        this.includes = includes;
    }
}

接著，我們可以深入瞭解主要的類：

public class Knapsack {  
    public static void main(String[] args) {
        Scanner scanner = new Scanner (System.in);

        System.out.println("Insert knapsack capacity:");
        int k = scanner.nextInt();

        System.out.println("Insert number of items:");
        int n = scanner.nextInt();

        System.out.println("Insert weights: ");
        int[] weights = new int[n + 1];

        for (int i = 1; i <= n; i++) {
            weights[i] = scanner.nextInt();
        }

        Element[][] elementMatrix = new Element[n + 1][k + 1];

        elementMatrix[0][0] = new Element(true);

        for (int i = 1; i <= k; i++) {
            elementMatrix[0][i] = new Element(false);
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= k; j++) {
                elementMatrix[i][j] = new Element(false);
                if (elementMatrix[i - 1][j].isExists()) {
                    elementMatrix[i][j].setExists(true);
                    elementMatrix[i][j].setIncludes(false);
                } else if (j >= weights[i]) {
                    if (elementMatrix[i - 1][j - weights[i]].isExists()) {
                        elementMatrix[i][j].setExists(true);
                        elementMatrix[i][j].setIncludes(true);
                    }
                }
            }
        }

        System.out.println(elementMatrix[n][k].isExists());
    }
}

唯一剩下的就是解決方案的重建，在上面的類中，我們知道解決方案是存在的，但是我們不知道它是什麼。

為了重建，我們使用下面的程式碼：

List<Integer> solution = new ArrayList<>(n);

if (elementMatrix[n][k].isExists()) {  
    int i = n;
    int j = k;
    while (j > 0 && i > 0) {
        if (elementMatrix[i][j].isIncludes()) {
            solution.add(i);
            j = j - weights[i];
        }
        i = i - 1;
    }
}

System.out.println("The elements with the following indexes are in the solution:\n" + (solution.toString()));

輸出：

Insert knapsack capacity:  
12  
Insert number of items:  
5  
Insert weights:  
9 7 4 10 3  
true  
The elements with the following indexes are in the solution:  
[5, 1]

揹包問題的一個簡單變化是在沒有價值優化的情況下填充揹包，但現在每個單獨專案的數量無限。

通過對現有程式碼進行簡單調整，可以解決這種變化：

// Old code for simplified knapsack problem
else if (j >= weights[i]) {  
    if (elementMatrix[i - 1][j - weights[i]].isExists()) {
        elementMatrix[i][j].setExists(true);
        elementMatrix[i][j].setIncludes(true);
    }
}

// New code, note that we're searching for a solution in the same
// row (i-th row), which means we're looking for a solution that
// already has some number of i-th elements (including 0) in it's solution
else if (j >= weights[i]) {  
    if (elementMatrix[i][j - weights[i]].isExists()) {
        elementMatrix[i][j].setExists(true);
        elementMatrix[i][j].setIncludes(true);
    }
}

5. 傳統的揹包問題

利用以前的兩種變體，現在讓我們來看看傳統的揹包問題，看看它與簡化版本的不同之處：

Given a set of items, each with a weight w1, w2... and a value v1, v2... determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit k and the total value is as large as possible.

在簡化版中，每個解決方案都同樣出色。但是，現在我們有一個找到最佳解決方案的標準（也就是可能的最大值）。請記住，這次我們每個專案都有無限數量，因此專案可以在解決方案中多次出現。

在實現中，我們將使用舊的類Element，其中添加了私有欄位value，用於儲存給定子問題的最大可能值:

public class Element {  
    private boolean exists;
    private boolean includes;
    private int value;
    // appropriate constructors, getters and setters
}

實現非常相似，唯一的區別是現在我們必須根據結果值選擇最佳解決方案：

public static void main(String[] args) {  
    // Same code as before with the addition of the values[] array
    System.out.println("Insert values: ");
    int[] values = new int[n + 1];

    for (int i=1; i <= n; i++) {
        values[i] = scanner.nextInt();
    }

    Element[][] elementMatrix = new Element[n + 1][k + 1];

    // A matrix that indicates how many newest objects are used
    // in the optimal solution.
    // Example: contains[5][10] indicates how many objects with
    // the weight of W[5] are contained in the optimal solution
    // for a knapsack of capacity K=10
    int[][] contains = new int[n + 1][k + 1];

    elementMatrix[0][0] = new Element(0);

    for (int i = 1; i <= n; i++) {
        elementMatrix[i][0] = new Element(0);
        contains[i][0] = 0;
    }

    for (int i = 1; i <= k; i++) {
        elementMatrix[0][i] = new Element(0);
        contains[0][i] = 0;
    }

    for (int i = 1; i <= n; i++) {
        for (int j = 0; j <= k; j++) {
            elementMatrix[i][j] = new Element(elementMatrix[i - 1][j].getValue());
            contains[i][j] = 0;

            elementMatrix[i][j].setIncludes(false);
            elementMatrix[i][j].setValue(M[i - 1][j].getValue());

            if (j >= weights[i]) {
                if ((elementMatrix[i][j - weights[i]].getValue() > 0 || j == weights[i])) {
                    if (elementMatrix[i][j - weights[i]].getValue() + values[i] > M[i][j].getValue()) {
                        elementMatrix[i][j].setIncludes(true);
                        elementMatrix[i][j].setValue(M[i][j - weights[i]].getValue() + values[i]);
                        contains[i][j] = contains[i][j - weights[i]] + 1;
                    }
                }
            }

            System.out.print(elementMatrix[i][j].getValue() + "/" + contains[i][j] + "  ");
        }

        System.out.println();
    }

    System.out.println("Value: " + elementMatrix[n][k].getValue());
}

輸出：

Insert knapsack capacity:  
12  
Insert number of items:  
5  
Insert weights:  
9 7 4 10 3  
Insert values:  
1 2 3 4 5  
0/0  0/0  0/0  0/0  0/0  0/0  0/0  0/0  0/0  1/1  0/0  0/0  0/0  
0/0  0/0  0/0  0/0  0/0  0/0  0/0  2/1  0/0  1/0  0/0  0/0  0/0  
0/0  0/0  0/0  0/0  3/1  0/0  0/0  2/0  6/2  1/0  0/0  5/1  9/3  
0/0  0/0  0/0  0/0  3/0  0/0  0/0  2/0  6/0  1/0  4/1  5/0  9/0  
0/0  0/0  0/0  5/1  3/0  0/0  10/2  8/1  6/0  15/3  13/2  11/1  20/4  
Value: 20

6. Levenshtein Distance

另一個使用動態規劃的非常好的例子是Edit Distance或Levenshtein Distance。

Levenshtein Distance就是兩個字串A,B,我們需要使用原子操作將A轉換為B：

  1. 字串刪除
  2. 字串插入
  3. 字元替換（從技術上講，它不止一個操作，但為了簡單起見，我們稱之為原子操作）

這個問題是通過有條理地解決起始字串的子串的問題來處理的，逐漸增加子字串的大小，直到它們等於起始字串。

我們用於此問題的遞迴關係如下：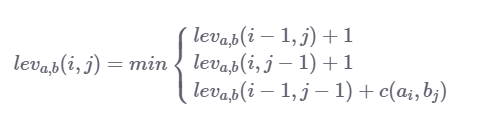

如果a == b則c（a，b）為0，如果a = = b則c（a，b）為1。

實現：

public class editDistance {  
    public static void main(String[] args) {
        String s1, s2;
        Scanner scanner = new Scanner(System.in);
        System.out.println("Insert first string:");
        s1 = scanner.next();
        System.out.println("Insert second string:");
        s2 = scanner.next();

        int n, m;
        n = s1.length();
        m = s2.length();

        // Matrix of substring edit distances
        // example: distance[a][b] is the edit distance
        // of the first a letters of s1 and b letters of s2
        int[][] distance = new int[n + 1][m + 1];

        // Matrix initialization:
        // If we want to turn any string into an empty string
        // the fastest way no doubt is to just delete
        // every letter individually.
        // The same principle applies if we have to turn an empty string
        // into a non empty string, we just add appropriate letters
        // until the strings are equal.
        for (int i = 0; i <= n; i++) {
            distance[i][0] = i;
        }
        for (int j = 0; j <= n; j++) {
            distance[0][j] = j;
        }

        // Variables for storing potential values of current edit distance
        int e1, e2, e3, min;

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                e1 = distance[i - 1][j] + 1;
                e2 = distance[i][j - 1] + 1;
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    e3 = distance[i - 1][j - 1];
                } else {
                    e3 = distance[i - 1][j - 1] + 1;
                }
                min = Math.min(e1, e2);
                min = Math.min(min, e3);
                distance[i][j] = min;
            }

        }

        System.out.println("Edit distance of s1 and s2 is: " + distance[n][m]);
    }
}

輸出：

Insert first string:  
man  
Insert second string:  
machine  
Edit distance of s1 and s2 is: 3

如果你想了解更多關於Levenshtein Distance的解決方案，我們在另外的一篇文章中用python實現了 Levenshtein Distance and Text Similarity in Python，
使用這個邏輯，我們可以將許多字串比較演算法歸結為簡單的遞迴關係，它使用Levenshtein Distance的基本公式

7. 最長共同子序列（LCS）

這個問題描述如下：

Given two sequences, find the length of the longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.

給定兩個序列，找到兩個序列中存在的最長子序列的長度。子序列是以相同的相對順序出現的序列，但不一定是連續的.

闡明：

如果我們有兩個字串s1="MICE"和s2="MINCE",最長的共同子序列是MI或者CE。但是，最長的公共子序列將是“MICE”，因為結果子序列的元素不必是連續的順序。

遞迴關係與一般邏輯：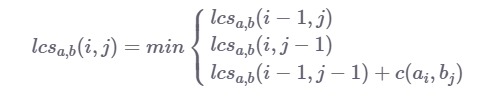

我們可以看到，Levenshtein distance和LCS之間只有微小的差別，特別是移動成本。

在LCS中，我們沒有字元插入和字元刪除的成本，這意味著我們只計算字元替換（對角線移動）的成本，如果兩個當前字串字元a [i]和b [j] 是相同的,則成本為1。

LCS的最終成本是2個字串的最長子序列的長度，這正是我們所需要的。

Using this logic, we can boil down a lot of string comparison algorithms to simple recurrence relations which utilize the base formula of the Levenshtein distance

使用這個邏輯，我們可以將許多字串比較演算法歸結為簡單的遞迴關係，它使用Levenshtein distance的基本公式。

實現：

public class LCS {  
    public static void main(String[] args) {
        String s1 = new String("Hillfinger");
        String s2 = new String("Hilfiger");
        int n = s1.length();
        int m = s2.length();
        int[][] solutionMatrix = new int[n+1][m+1];
        for (int i = 0; i < n; i++) {
            solutionMatrix[i][0] = 0;
        }
        for (int i = 0; i < m; i++) {
            solutionMatrix[0][i] = 0;
        }

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                int max1, max2, max3;
                max1 = solutionMatrix[i - 1][j];
                max2 = solutionMatrix[i][j - 1];
                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
                    max3 = solutionMatrix[i - 1][j - 1] + 1;
                } else {
                    max3 = solutionMatrix[i - 1][j - 1];
                }
                int tmp = Math.max(max1, max2);
                solutionMatrix[i][j] = Math.max(tmp, max3);
            }
        }

        System.out.println("Length of longest continuous subsequence: " + solutionMatrix[n][m]);
    }
}

輸出：

Length of longest continuous subsequence: 8

8.利用動態規劃的其他問題

利用動態規劃可以解決很多問題，下面列舉了一些：

  1. 分割槽問題：給定一組整數，找出它是否可以分成兩個具有相等和的子集
  2. 子集和問題：給你一個正整數的陣列及元素還有一個合計值，是否在陣列中存在一個子集的的元素之和等於合計值。
  3. 硬幣變化問題：鑑於給定面額的硬幣無限供應，找到獲得所需變化的不同方式的總數
  4. k變數線性方程的所有可能的解：給定k個變數的線性方程，計算它的可能解的總數
  5. 找到醉漢不會從懸崖上掉下來的概率：給定一個線性空間代表距離懸崖的距離，讓你知道酒鬼從懸崖起始的距離，以及他向懸崖p前進並遠離懸崖1-p的傾向，計算出他的生存概率

9.結論

動態程式設計是一種工具，可以節省大量的計算時間，以換取更大的空間複雜性，這在很大程度上取決於您正在處理的系統型別，如果CPU時間很寶貴，您選擇耗費記憶體的解決方案，另一方面，如果您的記憶體有限，則選擇更耗時的解決方案。

原文：https://stackabuse.com/dynamic-programming-in-java/

作者： Vladimir Batoćanin

譯者：lee

相關推薦

java動態規劃取硬幣問題

四種 ava exti 千萬 print light sca 小數 length 最近一直在研究動態規劃的問題。今天遇到了取硬幣問題。 其實動態規劃還是，我從底部向頂部，依次求出每個狀態的最小值，然後就可以標記上。 這道題目就是，假如有1,5,7,10這四種幣值的硬幣，我取

[leetcode] 45. 跳躍遊戲 II(Java)(動態規劃)

com max https 重疊 http findmi 條件 leetcode scrip 45. 跳躍遊戲 II 動態規劃 此題可以倒著想。 看示例： [2,3,1,1,4] 我們從後往前推，對於第4個數1，跳一次 對於第3個數1，顯然只能跳到第4個數上，那麽從第3個數

使用最小花費爬樓梯(Min Cost Climbing Stairs) Java動態規劃入門分析一

前言 題幹 陣列的每個索引做為一個階梯，第 i個階梯對應著一個非負數的體力花費值 cost[i](索引從0開始)。 每當你爬上一個階梯你都要花費對應的體力花費值，然後你可以選擇繼續爬一個階梯或者爬兩個階梯。 您需要找到達到樓層頂部的最低花費。

leetcode：解碼方法（java動態規劃）

package LeetCode; /* 一條包含字母 A-Z 的訊息通過以下方式進行了編碼： 'A' -> 1 'B' -> 2 ... 'Z' -> 26 給定一個只包含數字的非空字串，請計算解碼方法的總數。 示例 1: 輸入: "12" 輸出: 2 解釋: 它可以解碼為 "A

leetcode:不同路徑（java動態規劃）

一個機器人位於一個 m x n 網格的左上角 （起始點在下圖中標記為“Start” ）。 機器人每次只能向下或者向右移動一步。機器人試圖達到網格的右下角（在下圖中標記為“Finish”）。 問總共有多少條不同的路徑？ 例如，上圖是一個7 x 3 的網格。有多少可能的路徑？ 說明：m 和 n 的值均不

Combination Sum IV中兩種JAVA動態規劃解法的不同

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to

JAVA動態規劃（二）--最長公共子序列問題（LCS_subSequence）的三種解法與最長公共子字串（LCS_subString）的兩種解法與最長迴文串（LongestPalindrome）

動態規劃法 經常會遇到複雜問題不能簡單地分解成幾個子問題，而會分解出一系列的子問題。簡單地採用把大問題分解成子問題，並綜合子問題的解匯出大問題的解的方法，問題求解耗時會按問題規模呈冪級數增加。 為了節約重複求相同子問題的時間，引入一個數組，不管它們是否對最終

Java動態規劃

1. 介紹 動態規劃典型的被用於優化遞迴演算法，因為它們傾向於以指數的方式進行擴充套件。動態規劃主要思想是將複雜問題（帶有許多遞迴呼叫）分解為更小的子問題，然後將它們儲存到記憶體中，這樣我們就不必在每次使用它們時重新計算它們。 要理解動態規劃的概念，我們需要熟悉一些主題： 什

【Java】【滾動數組】【動態規劃】UVA - 11137 - Ingenuous Cubrency

得到 lose math scanner light clas details 狀態 ann 滾動數組優化自己畫一下就明白了。 http://blog.csdn.net/u014800748/article/details/45849217 解題思路：本題利用遞推關系解決。

java課作業一則:動態規劃(不優化)

tex value 交叉點 util 並且 class 分享圖片 and 簡單的 /* *1、實驗內容:1)第1題: *設平面上有一個m×n 的網格，將左下角的網格點標記為(0,0)而右上角的網格點標記為(m,n).某人想從(0,0)出發沿網格線行進到達(m,n).

java面試寶典page279 求數對之差的最大值(動態規劃)

package com.interview.datastructure; public class TestDynamicProgramming { //java面試寶典page279 求數對之差的最大值 //1.首先定義一個max方法來判斷儲存最大值 //2.如何構造動態規劃，如果原來

最長公共子序列（Java實現）——動態規劃

【問題描述】 給定2個序列X和Y，當另一序列Z既是X的子序列又是Y的子序列時，稱Z是序列X和Y的公共子序列。 給定2個序列X={A,B,C,B,D}和Y={B,D,C,A,B}，找出X和Y的最長公共子序列{B,C,B}。 【分析】最長公共子序列問題具有最優子結構性質 設 X = {

java斐波那契數列（Fibonacci sequence）的三種方式：遞迴，備忘錄，動態規劃

java斐波那契數列（Fibonacci sequence）的三種方式：遞迴，備忘錄，動態規劃 1.最常使用的是遞迴，就是從上往下尋找答案，然後在返回來。 2.備忘錄也是從上往下，只是去掉了遞迴中重複計算的部分，因為它使用一個容器來裝已經計算出的值，這裡就多一個判斷，如果計算過該式子，就直接

動態規劃之完全揹包問題（java實現）

之前寫了01揹包問題，現在寫完全揹包問題。和01揹包不同的是，完全揹包不限定某種物品的件數，可以裝0,1,2，...，而01揹包只有裝與不裝的區別。但是思考問題的方式還是一樣的，我就其中的最大值。詳細程式碼和註釋見下面程式碼。 package backpack; /* f[i][v]:前i件物

動態規劃--最長公共子序列（Java）

0.問題描述 給出兩個序列X,Y，求出他們的最長公共子序列及長度 1.分解最優解的結構 （1）若Xm =Yn ,且 Zk =Xm =Yn , 那麼 Zk-1 是 Xm-1 和 Yn-1 的最長公共子序列 （2）若Xm ≠ Yn ,且 Zk ≠ Xm , 那麼

動態規劃之揹包問題和區間模型--Java實現

揹包問題描述：給定n個重量為w1,w2...wn、價值為v1,v2...vn的物品和一個承重量為W的揹包，求這些物品中最優價值的一個子集，並且要能夠裝到揹包中。 結論：1.在不包括第i個物品的子集中，最優子集的價值是Value[i-1][j]. 2.在包括第i個物品的子

動態規劃--求目標值問題、找零錢問題以及求連續子陣列最大和 --java

1、動態規劃一般可分為線性動規，區域動規，樹形動規，揹包動規四類。 舉例: 線性動規:攔截導彈，合唱隊形，挖地雷，建學校，劍客決鬥等; 區域動規:石子合併， 加分二叉樹，統計單詞個數，炮兵佈陣等; 樹形動規:貪吃的九頭龍，二分查詢樹，聚會的歡樂，數字三角形等;

leetcode 44 ---- 動態規劃（困難） ：萬用字元匹配（java）

1.  問題：給定一個字串 (s) 和一個字元模式 (p) ，實現一個支援 '?' 和 '*' 的萬用字元匹配。 '?' 可以匹配任何單個字元。 '*' 可以匹配任意字串（包括空字串）。 兩個字串完全匹配才算匹配成功。 說明: s 可能為空，且只包含從 a-z 的小

藍橋杯-裝箱問題-動態規劃-java

問題描述 　　有一個箱子容量為V（正整數，0＜＝V＜＝20000），同時有n個物品（0＜n＜＝30），每個物品有一個體積（正整數）。 　　要求n個物品中，任取若干個裝入箱內，使箱子的剩餘空間為最小。 輸入格式 　　第一行為一個整數，表示箱子容量； 　　第二行為一個整數

（java）找出陣列中和為K的一組解（動態規劃）

考慮N個數的陣列A中是否存在和為K的解，可以分為考慮（N-1個數中是否有和為K的解）或者（N-1個數中是否有和為K-A[N-1]的解（解包含A[N-1]的情況））。也就是說，動態規劃方程是：P[N][K]=P[N-1][K]||P[N-1][K-A[N-1]]；直接上程式碼：