模式識別與機器學習 [國科大]

視屏連結

模式: 為了能夠讓機器執行和完成識別任務，必須對分類識別物件進行科學的抽象，建立它的數學模型，用以描述和代替識別物件，這種物件的描述即為模式。

模式識別系統過程：

1. 特徵提取與選擇
   
2. 訓練學習
   
3. 分類識別

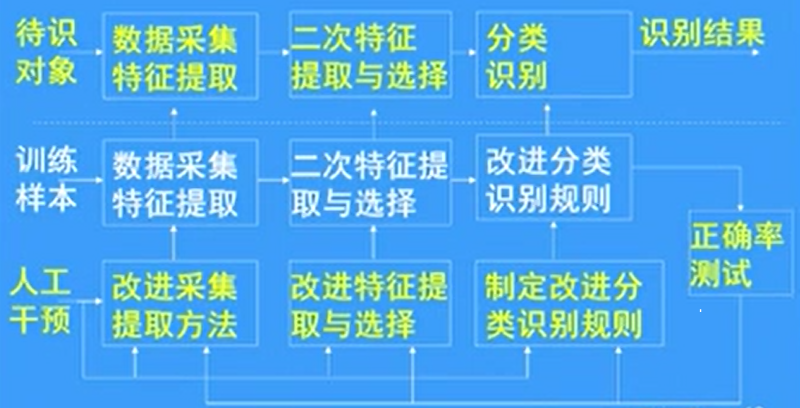
模式識別過程從資訊層次、形態轉換上講，是由分析物件的物理空間通過特徵提取轉換為模式的特徵空間，然後通過分類識別轉換為輸出的類別空間。

特徵提取是對研究物件本質的特徵進行量測並講結果數值化或將物件分解並符號化，形成特徵向量、符號串或關係圖，產生代表物件的模式。

特徵選擇是在滿足分類識別正確率的條件下，按某種準則儘量選用對正確分類識別作用較大的特徵，從而用較少的特徵來完成分類識別任務。

在模式採集和預處理中，一般要用到模數(A/D)轉換。A/D轉換必須注意：

1. 取樣率，必須滿足取樣定理
   
2. 量化等級，取決於精度要求

在資料採集過程中，一般我們會進行一些預處理過程，如

1. 去噪聲：消除或減少模式採集中的噪聲及其它干擾，提高信雜比(信噪比)
   
2. 去模糊：消除或減少資料影象模糊及幾何失真，提高清晰度
   
3. 模式結構轉換：例如把非線性模式轉變為線性模式，以利於後續處理，等等

預處理的方法包括: 濾波，變換，編碼，歸一化等

特徵提取/選擇的目的： 降低維數，減少記憶體消耗，使分類錯誤減小

分類: 把特徵空間劃分成類空間，影響分類錯誤率的因數：

1. 分類方法
   
2. 分類器的設計
3. 提取的特徵
   
4. 樣本質量

模式識別的主流技術有：

1. 統計模式識別
2. 結構模式識別
   
3. 模糊模式識別
4. 人工神經網路方法
   
5. 人工智慧方法
   
6. 子空間法

統計模式識別直接利用各類的分佈特徵或隱含地利用概率密度函式、後驗概率等概念進行分類識別。基本的技術有聚類分析、判別類域代數介面法、統計決策法、最近鄰法等。

結構模式識別將物件分解為若干基本單元，即基元；其結構關係可以用字串或圖來表示，即句子；通過對句子進行句法分析，根據文法而決定其類別。

模糊模式識別將模式或模式類作為模糊集，將其屬性轉化為隸屬度，運用隸屬函式、模糊關係或模糊推理進行分類識別。

人工神經網路方法由大量的基本單元，即神經元互聯而成的非線性動態系統。

人工智慧方法研究如何是機器具有人腦功能的理論和方法，故將人工智慧中有關學習、知識表示、推理等技術用於模式識別。

子空間法根據各類訓練樣本的相關陣通過線性變換由原始模式特徵空間產生各類對應的子空間，每個子空間與每個類別一一對應。

特徵向量一個分析物件的n個特徵量測值分別為 \(x_1,x_2,...,x_3\)，它們構成一個n維特徵向量\(x\)，\(x = (x_1,x_2,...,x_n)^T,x\)是原物件(樣本)的一種數學抽象，用來代表原物件，即為原物件的模式。

特徵空間對某物件的分類識別是對其模式，即它的特徵向量進行分類識別。各種不同取值的\(x\)的全體構成了\(n\)維空間，這個\(n\)維空間稱為特徵空間，不同場合特徵空間可記為 \(X^n, R^n\)或\(\Omega\)。特徵向量\(x\)便是特徵空間中的一個點，所以特徵向量有時也稱為特徵點。

隨機變數由於量測系統隨機因素的影響及同類不同物件的特徵本身就是在特徵空間散步的，同一個物件或同一類物件的某特徵測值是隨機變數。由隨機分量構成的向量稱為隨機向量。同一類物件的特徵向量在特徵空間中是按某種統計規律隨機散步的。

協方差矩陣和自相關矩陣都是對稱矩陣。設\(A\)為對稱矩陣，對任意的向量\(x, x^TAx\)是\(A\)的二次型。若對任意的\(x\)恆有：
\[ x^TAx \geq 0 \]
則稱\(A\)為非負定矩陣。協方差矩陣是非負定的。

獨立必不相關，反之不一定。

在正態分佈的情況下，獨立於不相關是等價的。

聚類分析概念

聚類分析基本思想:
假設 物件集客觀存在著若干個自然類，每個自然類中個體的某些屬性具有較強的相似性。
原理 將給定模式分成若干組，每組內的模式是相似的，而組間各模式差別較大。

該方法的有效性取決於分類演算法和特徵點分佈情況的匹配。
分類無效的情況有：

1. 特徵選取不當使分類無效；
   
2. 特徵選擇不足可能使不同類別的模式判為一類；
3. 特徵選取過多可能無益反而有害，增加分析負擔並使分析效果變差；
4. 量綱選擇不當。

聚類分析過程：

1. 特徵提取
   
2. 模式相似性度量
   
3. 點與類之間的距離
   
4. 類與類之間的距離
5. 聚類準則及聚類演算法
6. 有效性分析

模式相似性測度

模式相似性測度方法

1. 距離測度
   
2. 相似測度
3. 匹配測度

距離測度
測度基礎： 兩個向量矢端的距離
測度數值：兩向量各相應分量之差的函式

歐式(Euclidean)距離
\[ d(\vec x, \vec y) = ||\vec x - \vec y|| = [\sum^n_{i=1}(x_i - y_i)^2]^\frac{1}{2} \\ \vec x = (x_1,x_2,...,x_n), \vec y = (y_1, y_2,...,y_n) \]

絕對值距離(Manhattan距離)
\[ d(\vec x, \vec y) = \sum^n_{i=1} |x_i - y_i| \]

切氏(Chebyshev)距離
\[ d(\vec x, \vec y) = \max_i |x_i - y_i| \]

明(Minkowski)氏距離
\[ d(\vec x, \vec y) = [\sum_{i=1}^n|x_i - y_i|^m]^{1/m} \]

馬氏(Mahalanobis)距離
設n維向量\(\vec x_i\)和\(\vec x_j\)是向量集\({\vec x_1, \vec x_2,...,\vec x_m}\)中的兩個向量，馬氏距離\(d\)定義為
\[ d^2(\vec x_i, \vec x_j) = (\vec x_i - \vec x_j)^`V^{-1}(\vec x_i - \vec x_j) \]
其中
\[ V = \frac{1}{m-1} \sum^m_{i=1}(\vec{x_i} - \overline{\vec{x}})^` \\ \overline{\vec{x}} = \frac{1}{m} \sum^m_{i=1} {\vec x_i} \]
馬氏距離具有平移不變性。
對於 \(\vec y = \vec x\)進行類變換即\(\vec y = A\vec x\),其中\(A\)為非奇異矩陣，馬氏距離不變。

馬氏距離的性質: 對於一切非奇異線性變化都是不變的。即，具有座標系比例、旋轉、平移不變性，並且從統計意義上儘量去掉了分量間的相關性。

例題

模式相似性測度
測度基礎: 以兩向量的方向是否相近作為考慮的基礎，向量長度並不重要。設
\[ \vec x = (x_1, x_2, ...,x_n), \vec y = (y_1,y_2,...,y_n) \]

1. 角度相似係數
   \[ cos(\vec x, \vec y) = \frac{\vec x \vec y}{||\vec x|| ||\vec y||} = \frac{\vec x \vec y}{[(\vec x^` \vec x)(\vec x^` \vec x)]^{1/2}} \]
   注意：座標系的旋轉和尺度的縮放是不變的，但對一般的線性變換和座標系的平移不具有不變性。

2. 相關係數
   實際上是資料中心化後的向量夾角餘弦
   \[ r(\vec x, \vec y) =\frac{(\vec x - \overline{\vec x})^`(\vec y - \overline{\vec y})}{[(\vec x - \overline{\vec x})^`(\vec x - \overline{\vec x})(\vec y - \overline{\vec y})^`(\vec y - \overline{\vec y})]^{\frac{1}{2}}} \]
   相關係數的取值在 [-1，1]，取值為1時，兩組資料最相關。

3. 指數相似係數
   \[ e(\vec x, \vec y) = \frac {1}{n} \sum^n_{i=1} exp[-\frac{3(x_i-y_i)^2}{4 \sigma^2_i}] \]

式中\(\sigma^2_i\)為相應分量的協方差，\(n\)為向量維度，它不受量綱變化的影響。

1. 匹配測度
   當特徵只有兩個狀態(0, 1)時，常使用匹配測度。0表示無此特徵，1表示有此特徵，故稱之為二值特徵。對於給定的\(x\)和\(y\)中的某兩個相應分量\(x_i\)與\(y_j\)：
   若\(x_i=1,y_j=1\)，則稱\(x_i\)與\(y_j\)是(1-1)匹配；
   若\(x_i=1,y_j=0\)，則稱\(x_i\)與\(y_j\)是(1-0)匹配；
   若\(x_i=0,y_j=1\)，則稱\(x_i\)與\(y_j\)是(0-1)匹配；
   若\(x_i=0,y_j=0\)，則稱\(x_i\)與\(y_j\)是(0-0)匹配。

對於二值\(n\)維特徵向量可定義如下相似性測度
令 \(a = \sum_i x_iy_i\) 為\(\vec x\)與\(\vec y\)的(1-1)匹配的特徵數目
令 \(b = \sum_i y_i(1-x_i)\) 為\(\vec x\)與\(\vec y\)的(0-1)匹配的特徵數目
令 \(c = \sum_i x_i (1-y_i)\) 為\(\vec x\)與\(\vec y\)的(1-0)匹配的特徵數目
令 \(e = \sum_i (1-x_i)(1-y_i)\) 為\(\vec x\)與\(\vec y\)的(0-0)匹配的特徵數目

Tanimoto測度
\[ s(\vec x, \vec y) = \frac {a}{a+b+c} = \frac {\vec x^`\vec y}{\vec x^` \vec x + \vec y^` \vec y - \vec x^` \vec y} \]

例題

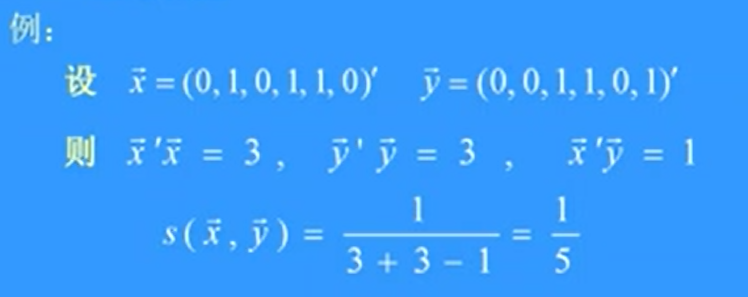
可以看出，它等於共同具有的特徵數目與分別具有的特徵種類數目之比。這裡只考慮了(1-1)匹配而不考慮(0-0)匹配。

Rao測度
\[ s(\vec x, \vec y) = \frac{a}{a+b+c+e} = \frac{\vec x^` \vec y}{n} \]

注：(1-1)匹配特徵數目和所選用的特徵數目之比

簡單匹配係數
\[ m(\vec x, \vec y) = \frac {a+e}{n} \]
注：上式分子為(1-1)匹配特徵數目與(0-0)匹配特徵數目之和，分母為所考慮的特徵數目。

Dice係數

\[ m(\vec x, \vec y) = \frac{a}{2a+b+c} = \frac{\vec x^` \vec y}{\vec x^` \vec x + \vec y^` \vec y} = \frac {(1-1)匹配個數}{兩向量中1的總數} \]

Kulzinsky係數
\[ m(\vec x, \vec y) = \frac{a}{b+c} = \frac{\vec x^` \vec y}{\vec x^` \vec x + \vec y^` \vec y - 2\vec x^` \vec y} = \frac{(1-1)匹配個數}{(0-1)+(1-0)匹配個數} \]

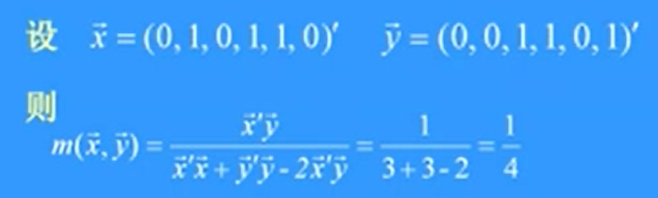
類的定義
定義1
若集合S中任意兩個元素\(x_i,x_i\)的距離\(d_{ij}\)有
\[ d_{ij} \leq h \]
則稱S相對於闕值h組成一類。

定義2
若集合S中任一元素\(x_i\)與其他各元素\(x_j\)間的距離\(d_{ij}\)均滿足
\[ \frac{1}{k-1} \sum_{x_j \in S} d_{ij} \leq h \]
則稱S相對於闕值h組成一類(k為集合元素個數)

定義3
若集合S中任意兩個元素\(x_i, x_j\)的距離\(d_{ij}\)滿足
\[ \frac {1}{k(k-1)} \sum_{x_i \in S} \sum_{x_j \in S} d_{ij} \leq h 且 d_{ij} \leq r \]
則稱S相對於闕值h,r組成一類

定義4
若集合S中元素滿足對於任一 \(x_i \in S\)，都存在某 \(x_j \in S\)使它們的距離
\[ d_{ij} \leq h \]
則稱S相對於闕值h組成一類。