排序演算法——分治思想與歸併排序

1、分治法思想

分治思想主要通過遞迴來實現，每層遞迴中主要包括三個步驟：

分解：即將原問題劃分為若干子問題，子問題的形式要保證和原問題一致，但規模更小。
解決：當劃分子問題的規模足夠小時，停止遞迴，求解子問題，獲取子問題的解決結果並返回給上一層。
合併：將子問題的解決結果進行合併，得到原問題的解。

也就是說，分治思想就是將一個大問題用過遞迴層層分解為無數個子問題，這些子問題要保證與與原問題是一個型別，只不過規模更小更加容易求解，但求解過程相同。

2、歸併排序演算法思想

1、思考：如果給了我們兩個已經做好排序的陣列（相同排序規則）A和B，我們該如何將其合併到一個有序陣列C？

這個問題很簡單，依次從兩個陣列中取元素比較然後放進C中即可。而如果A、B陣列都只有一個元素時，他們都成為了一個有序陣列，則可以直接進行比較放在陣列C中，返回有序的陣列C。

2、通過分治思想對無序陣列排序問題進行劃分：對於一個無序的陣列array

（1）分解：通過遞迴將無序陣列進行劃分，每次從array.length/2處劃分為兩個陣列，直到劃分後的子陣列規模為1。

（2）解決：當子陣列規模為1時，此時的最小規模陣列已經自動變為一個有序陣列，遞迴終止返回有序陣列結果。

（3）合併：接收下一層遞迴所返回的兩個有序子陣列，將這兩個有序子陣列的資料進行合併為一個新的有序陣列，然後返回該有序陣列給上一層遞迴。

3、排序例項：為方便理解遞迴劃分陣列，可以建立一個遞迴樹形圖（理解遞迴比較方便）。以陣列int[] arr = {3,23,4,13,4,5,63,6,2}為例，其陣列劃分樹形圖為

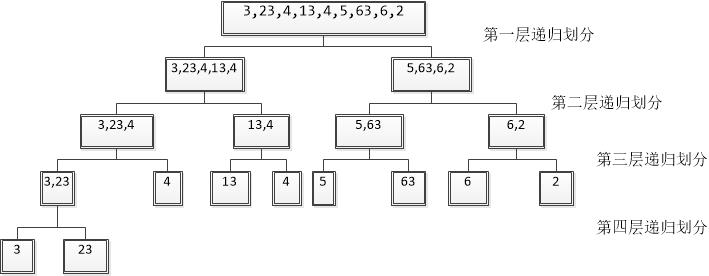
那麼接下來就是將葉子節點已經排序好的陣列返回給上一層遞迴，在上一層中處理合並一個新的有序陣列再返回給上一層，重複該步驟直到根節點層就可以將原陣列變為一個有序陣列。

也就是說，歸併演算法中遞迴呼叫的方法主要為兩部分，分別是分割陣列以及數組合（將兩個有序陣列進行合併）。虛擬碼如下

merge(int[] arr){
    if(arr.length < 2){
        return arr;//如果傳入的陣列長度為1那麼就直接返回
    }
    int[] left = splitLeft(arr);//劃分獲取左子陣列
    int[] right = spliteRight(arr);//劃分獲取右子陣列
    
    left = merge(left);//遞迴呼叫，獲得排序後的左子陣列
    right = merge(right);//遞迴呼叫，獲得排序後的右子陣列
    
    arr = sort(left,right);//將左右有序子數組合併為一個有序陣列
    return arr;//返回
}

具體程式碼實現（個人寫的依據演算法邏輯思想寫的一個示例，劃分左右子陣列都是新建立陣列進行賦值，空間複雜度很高，而且提高了時間複雜度，但是主要是便於理解）

個人實現：

/**
 * 
 * @Description:分治演算法，利用遞迴，將一個數組元素不斷的分割為兩個陣列，直到陣列分割到只剩下一個元素
 * 然後返回給上一層，主要是保證返回給上一層中的兩個陣列是已經排好序的陣列，在上一層中進行排序合併，然後再返回
 * 就可以最終得到一個有序陣列
 */
public class Sort {
    public static int[] merge(int[] arr){
        
        int left = 0;
        int right = arr.length;
        if (right == 1) {
            int[] endArr = {arr[left]};
            return endArr;
        }
        
        //陣列劃分
        int mid = (left + right) / 2;
        int[] leftArr = new int[mid-left];
        int[] rightArr = new int[right - mid];
        for (int i = 0; i <= mid-1; i++) {
            leftArr[i] = arr[i];
        }
        for (int i = 0,j=mid; i < rightArr.length && j < arr.length; i++,j++) {
            rightArr[i] = arr[j];
        }
        
        //遞迴呼叫，獲取排序完成的左右子陣列
        leftArr = merge(leftArr);
        rightArr = merge(rightArr);
        
        //合併兩個陣列並排序
        return sort(arr, leftArr, rightArr);
    }
    public static int[] sort(int[] arr, int[] left, int[] right){
        int i = 0;
        int j = 0;
        for (int index = 0; index < arr.length; index++){
            if (i >= left.length && j < right.length) {
                arr[index] = right[j];
                j++;
                continue;
            }
            if (j >= right.length && i < left.length) {
                arr[index] = left[i];
                i++;
                continue;
            }
            if (left[i] > right[j]){
                arr[index] = right[j];
                j++; 
            } else {
                arr[index] = left[i];
                i++;
            }
        }
        return arr;
    }
    public static void main(String[] args) {
        int[] arr = {3,23,4,13,4,5,63,6,2};
        for(int i:merge(arr)) {
            System.out.println(i);
        }
    }
}

較好的實現：

public class Solution {
    /*
     * @param A:an integer array
     * @return:
     */
    public voidsortIntegers2(int[] A) {
        // writeyour code here
        //利用歸併排序對陣列A進行排序
       mergeSort(A,0,A.length-1);
    }
    //歸併排序
    public void mergeSort(int[] A,int start,int end){
       if(start>=end) return;
        int middle= (start+end)/2;
       mergeSort(A,start,middle);
       mergeSort(A,middle+1,end);
        //歸併排序需要分配的臨時陣列
        //這是歸併排序的核心
        int []temp  = new int[end-start+1];
        inti=start;
        int j =middle+1;
        intindex=0;
       while(i<=middle&&j<=end){
           if(A[i]<=A[j]){
               temp[index++] = A[i++];
            }else{
               temp[index++] = A[j++];
            }
        }
       while(i<=middle){
           temp[index++] =A[i++];
        }
       while(j<=end){
           temp[index++] =A[j++];
        }
        i=start;
        index = 0;
       for(;i<=end;i++){
            A[i] =temp[index++];
        }
    }
}

排序演算法——分治思想與歸併排序

1、分治法思想分治思想主要通過遞迴來實現，每層遞迴中主要包括三個步驟：分解：即將原問題

快速排序演算法-分治思想

以下內容全部轉載自:http://www.cnblogs.com/luchen927/archive/2012/02/29/2368070.html 今天介紹快速排序，這也是在實際中最常用的一種排序演算法，速度快，效率高。就像名字一樣，快速排序是最優秀的一種排序演算法。

排序演算法（四）——歸併排序與遞迴

基本思想分析歸併排序之前，我們先來了解一下分治演算法。分治演算法的基本思想是將一個規模為N的問題分解為K個規模較小的子問題，這些子問題相互獨立且與原問題性質相同。求出子問題的解，就可得到原問題的解。分治演算法的一般步驟：（1）分解，將要解決的問題劃分成若干規模較小

java排序演算法（四）------歸併排序

歸併排序：是利用歸併的思想實現的排序方法，該演算法採用經典的分治（divide-and-conquer）策略（分治法將問題分(divide)成一些小的問題然後遞迴求解，而治(conquer)的階段則將分的階段得到的各答案"修補"在一起，即分而治之)。合

排序演算法c語言描述---歸併排序

排序算法系列學習，主要描述氣泡排序，選擇排序，直接插入排序，希爾排序，堆排序，歸併排序，快速排序等排序進行分析。文章規劃：一。通過自己對排序演算法本身的理解，對每個方法寫個小測試程式。具體思路分析不展開描述。二。通過《大話資料結構》一書的截圖，詳細分析該演算法。在此，推薦

排序演算法：二路歸併排序（java）

public class MergeSort { /** * * @param array 待排序陣列 * @param temp 輔助陣列 * @param start 開始下標 * @param end 結束下標

五十道程式設計小題目 --- 28 八大排序演算法 java 之 07歸併排序

7. 歸併排序（Merge Sort）基本思想：歸併（Merge）排序法是將兩個（或兩個以上）有序表合併成一個新的有序表，即把待排序序列分為若干個子序列，每個子序列是有序的。然後再把有序子序列合併為整體有序序列。歸併排序示例：合併方法：設r[

常見比較排序演算法的實現（歸併排序、快速排序、堆排序、選擇排序、插入排序、希爾排序）

這篇部落格主要實現一些常見的排序演算法。例如： //氣泡排序 //選擇排序 //簡單插入排序 //折半插入排序 //希爾排序 //歸併排序 //雙向的快速排序（以及快速排序的非遞迴版本） //單向的快速排序 //堆排序對於各個演算法的實現

排序演算法（七）——歸併排序

歸併排序（Merge Sort）演算法就是將多個有序資料表合併成一個有序資料表。如果參與合併的只有兩個有序表，則稱為二路合併。對於一個原始的待排序序列，往往可以通過分割的方法來歸結為多路合併排序。合併排序演算法的運作如下：（1）首先將含有n個結點的待排序資料序列看成9個長度為1的有序子表

歸併排序演算法原理分析與程式碼實現

歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法（Divide and Conquer）的一個非常典型的應用，歸併排序將兩個已排序的表合併成一個表。歸併排序基本原理

跟著《演算法導論》學習——插入排序與歸併排序

讀前宣告：本人所寫帖子主要為了記錄本人學習的一個過程，無他想法，由於內容比較膚淺，如有雷同，非常正常！！！本文內容：本文主要是參考《演算法導論》這本書，完成部分演算法編寫，可能程式設計習慣或者風格比較差，還請多多批評。 1、插入排序（Insertion Sort）插入

C語言排序（五)——插入排序與歸併排序演算法比較

一.實驗內容： 1、編寫函式分別實現插入排序和歸併排序演算法 2、編寫主函式通過呼叫函式實現對待排資料的呼叫 3、待排資料利用隨機函式迴圈產生10萬個以上的資料 4、利用求系統時間的函式，分別求出2個排

分治演算法的完美使用----歸併排序

歸併排序（Merge Sort）演算法完全依照了分治模式　　分解：將 n 個元素分成各含 n/2 個元素的子序列；　　解決：對兩個子序列遞迴地排序；　　合併：合併兩個已排序地子序列以得到排序結果；和快速排序不同的是　　歸併的劃分比較隨意，快排重點就是劃分　　歸併的重點就是合併，快排不需要合併程式

O(n*logn)級別的演算法之二（快速排序）的三種實現方法詳解及其與歸併排序的對比

快速排序被稱為二十世紀演算法界的一大傑作一，單路快排 1.測試用例： #ifndef INC_06_QUICK_SORT_DEAL_WITH_NEARLY_ORDERED_ARRAY_SORTTESTHELPER_H #define INC_06_QUICK_

分治演算法（一）--歸併排序

歸併排序最近上演算法課，老師講到分治演算法那塊了，感覺上課是認真聽了的，可是那個段子手老師講幾個笑話我就忘完了，很尷尬，所以以後她每講一章，自己還是總結下哈分治演算法的理解就我個人來說，對分治演算法理解很簡單，就三個字分解合分：就是把大

演算法分析——分治思想之快速排序

優化一個演算法的最根本的原理就是減少演算法的基本操作。分治法的設計思想是，將一個難以直接解決的大問題，分割成一些規模較小的相同問題，以便各個擊破，分而治之。於是，在快速排序中，我們通過分割陣列的思路來將大問題分割成小規模的問題，與二分搜尋法類似的是，在二分法中，我們需

常見排序演算法總結分析之選擇排序與歸併排序-C#實現

本篇文章對選擇排序中的簡單選擇排序與堆排序，以及常用的歸併排序做一個總結分析。 [常見排序演算法總結分析之交換排序與插入排序-C#實現](https://www.cnblogs.com/iwiniwin/p/12589405.html)是排序演算法總結系列的首篇文章，包含了一些概念的介紹以及交換排序（冒泡與

演算法-優先佇列與堆排序

優先佇列許多應用程式都需要處理有序的元素，但不一定要求他們全部有序，或是不一定要一次就將他們排序。很多情況下我們會收集一些元素，處理當前鍵值最大的元素，然後再收集更多元素，再處理當前鍵值最大的元素，如此這般。在這種情況下，一個合適的資料結構應該支援兩種操作：刪除最大元素和插入元素。

從零開始學演算法（四）歸併排序

從零開始學演算法（四）歸併排序歸併排序演算法介紹演算法原理演算法簡單記憶說明演算法複雜度和穩定性程式碼實現歸併排序程式碼是Javascript語言寫的（幾乎是虛擬碼）演算

演算法第五記-歸併排序

今天我要講的排序演算法是歸併排序，首先我想提出一個問題（很多演算法題的思路都源於此），給定兩個已排序的序列，如何將其兩個序列合併為一個大序列並且依然保持有序。思路很簡單每個小序列維持一個指標指向左邊界，然後兩個序列的左邊界進行比較大小，小的那方加入新的序列中

排序演算法——分治思想與歸併排序

1、分治法思想

2、歸併排序演算法思想

相關推薦