宣告：本文嚴禁轉載

0.前言：

數學期望當前在OI中是一個類似於數論方面門檻的知識，在競賽中有考察。本文將詳細的講解此內容，但也不是隻糾纏於簡單的概念，而會解決一些題目.可能這樣介紹的知識對於大佬來說還是比較基礎，但對像我這樣的萌新來說通俗易懂，所以請各位大佬不要噴我。

1.什麼是期望?

日常生活中，我們每做一件事，都有對它的期望，這裡的期望不僅僅只結果的勝負之類，也可以與狀態有關。但在OI中，一般指的就是達到結果的期望，最樸素的計算是每次可能結果的概率乘以其結果的總和

這是最基本的數學特徵。

廣義下的定義：一次隨機抽樣中所期望的某隨機變數的取值。

數學定義：

2.引入：

問題1：

先看一個問題：

甲乙兩個正常人賭博，丙作為裁判監督，五局三勝，贏家可以獲得100元的獎勵。當比賽進行到第四局的時候，甲勝了兩局，乙勝了一局，但這時賭場遇到了警察的查封，丙見勢不妙，立馬逃走了，甲乙兩人被迫中止了比賽，那麼，如何分配這100元？（每局都能分出勝負）

方案1：

每人50元。

這顯然是和平解決問題的方式，此時乙會贊成，但是甲一定有意見，顯然，自己已經拿下賽點，不可能心甘情願的平均分錢。

方案2：

按照獲勝的概率分。

假設比賽繼續進行，那麼下一輪：

50%:甲贏，拿下100元。

50%：乙贏，繼續比賽。

但是，如果問題就進行到這裡，也就沒有接下來的期望了。

當然，如果乙在暗中操縱下贏了，那麼再下一輪中，

甲乙兩人都有50%的概率獲勝，拿下100元。

甲乙：？？這怎麼算？

再次觀察。

假設甲最終在想象中輸了，那麼他是在什麼概率下輸的呢？

\(\frac{1}{2}\times \frac{1}{2}=\frac{1}{4}\)

他實際上只有四分之一的概率輸。

顯而易見，因為每局都能分出勝負，所以他有\(\frac{3}{4}\)的概率贏掉。

那麼情況就簡單了，我們根據他們的勝率來分錢。

甲分\(100\times \frac{3}{4}=75\)元

乙分\(100\times \frac{1}{4}=25\)元

此遊戲完結~

問題2：

一位公司招募員工，幾乎沒有什麼面試，甲乙兩個年輕人就意外的獲得了一份工作，這時，面試官卻說要給他們發入司獎金，每人需要從各自的三個紅包中選擇一個。

此時，他們已知紅包中有一個1000元的，兩個500元的。

兩位年輕人各自抽取了一個。

他們剛要開啟紅包，面試官卻制止了他們，隨機開啟每人剩下紅包中的一個，相同的，裡面都裝著500元錢。

於是面試官向他們詢問：如果同意你們用手上的紅包換取未開啟的紅包，你會換嗎？

乍一看，這是一個無厘頭的問題，可能有些意氣風發的人便想到堅持自我等諸多大道理，或者暗自猜測面試官在紅包上做了什麼標記。

但也有些人想把握機會。

湊巧，甲堅持了原來的選擇，乙卻嘗試了機會。

表面上看，這是一個完全機會均等，拼手氣的選擇。

但真的是這樣嗎？

稍加理性分析，我們可以得到一個初步的結論，幫助我們做出選擇：

如果員工剛開始恰巧選擇了1000元，他不交換會得到1000元，而顯然有更大概率他剛開始選到了500元，那麼他相應的就只能得到500元了。

由此，選擇交換會獲得更大的收益。

當然，我們可以不僅僅停留在定向判斷。

下面定量計算一下：

設為A，B，C三個紅包

當員工選擇了A紅包後，就將三個紅包分為兩組，第一組為A紅包，第二組為B、C紅包。很明顯1000元在第一組的概率為\(\frac{1}{3}\)，在第二組的概率為\(\frac{2}{3}\)，而面試官打開了B紅包，發現B為500元紅包，這裡其實是幫助員工在第二組裡篩選掉了一個錯誤答案，所以1000元在C紅包的概率其實為\(\frac{2}{3}\)。

所以就要換嘍

當然，看到是面試官來做這個實驗就知道這還是一個面試環節

於是甲就被炒魷魚了

但是，當甲走到門口時，面試官靈機一動，告訴他可以再回答一個問題。

於是甲滿懷激動地走了過來。

面試官把向兩人踢出提出了下一個問題：

如果給你手上的紅包，讓你換已經開啟的呢？（開啟的那個是500元）

顯然無論如何都是不換的於是兩人完美的成為了同事

面試官因招到了人完美的收到了4000元

3.例題1：

剛才的故事就是數學期望的一個簡單應用，兩個人都有對自己贏錢的期望（理性分析），便成功的解決了問題。

但是對模型：每次可能結果的概率乘以其結果的總和

的使用卻並不是很明顯

那麼

下面給出一道入門題目，可用以上知識解決：

戳

• 題意簡敘：

一個01串中每個長度為\(X\)的全1子串可貢獻\(X^3\)的分數。

給出n次操作的成功率\(p[i]\)，求期望分數。

分析：

我們可以觀察到每次對答案的貢獻是三次方級別的。

吼啊，我不會三次方期望啊。

仔細觀察，首先發現一次方的期望是很好弄的。

於是設\(a[i]\)表示前i位中第i位為1的長度的期望：

則有

\[a[i]=(a[i-1]+1)\times p[i]\]

tag：即為在i-1的末尾加一個概率為\(p[i]\)出現的1

接著推平方

設\(b[i]\)表示前i位中第i位為1的長度的平方的期望：

則有

\[b[i]=(b[i-1]+2\times a[i-1]+1)\times p[i]\]

tag:期望的線性延伸：

\[x^2->(x+1)^2->x^2+2x+1\]

運用這種方法，我們可以在求出\(a[i]\)的基礎上推出\(b[i]\)

同理，設\(f[i]\)表示前i位中第i位為1的長度的立方的期望：

則有：

\[f[i]=(f[i-1]+3\times b[i-1]+3\times a[i-1]+1)\times p[i]\]

• 哇塞我要A紫題了！！！

然後在滿心歡喜的提交上去後發現wa了。

顯然，我們還有沒考慮到的地方？

是什麼呢？

是最後求得的答案與中間過渡式子的不同性。

其實，前三個式子我們都只考慮第i位，這樣做是為了遞推下面的式子，但是答案讓我們求出最終的期望分數，也就是前n位，這時輸出f[n]自然就炸了。

所以，只需把三次方遞推式稍微變形一下即可；

\[f[i]=(f[i-1]+3\times b[i-1]+3\times a[i-1]+1)\times p[i]+f[i-1]\times (1-p[i])=f[i-1]+(3\times b[i-1]+3\times a[i-1]+1)\times p[i]\]

這樣最終的\(f[n]\)就是答案嘍！

code：

//AC記錄：https://www.luogu.org/record/21569138
#include<cstdio>
using namespace std;
double a[100005],b[100005],f[100005],p[100005];
int main()
{
    int n;
   scanf("%d",&n);
   for(int i=1;i<=n;i++)
    {
       scanf("%lf",&p[i]);
       a[i]=(a[i-1]+1)*p[i];
       b[i]=(b[i-1]+2*a[i-1]+1)*p[i];
       f[i]=f[i-1]+(3*b[i-1]+3*a[i-1]+1)*p[i];
   }
   printf("%.1lf\n",f[n]);
   return 0;
}

學好數學期望，遞推AC紫題！(其實這應該算dp

4.例題2：

思考題：

tag：這道題筆者並沒有找到題目出處，如有發現者，歡迎在評論區留言！

• 給定一個無向圖，每個點可以等概率地走到與它有邊的點

• 求從1走到n所需要的期望步數

• N<=500

分析：

• \(F[i]\)表示從i走到n的期望步數

• \(F[n]=0\);

• \(F[i]=aver\){\(f[j]\)}\(+1\),\((i,j)\)有邊

tag：

天哪上面這張圖小的洛谷都水印不上了？？

• 構成n元一次方程組

• 高斯消元？

5.例題3

https://www.luogu.org/problem/P2911

我怎麼開始講紅題了真是trl

• 題意簡敘：

三個骰子，每個面的概率均等，顯然，三個面相加能得到一個唯一的數，而得到這個唯一的數卻有多種不同的組合方法。

現在你需要求出哪個和出現的概率最大。

解法1：

這題的資料範圍很小，直接暴力跑三重迴圈就行了。

解法2：

這裡我閒的沒事用了與期望相關的知識來簡化了一下。但是這裡只是定向的判斷一下。

直接計算骰子的期望，得：

\[\frac{(a+b+c+3)}{2}\]

但是這個想法卻有考慮不周的情況，這裡留給讀者思考。

6.例題4

題目連結：

https://www.luogu.org/problem/UVA10288

• 題意簡敘：

每張彩票上有一個漂亮圖案，圖案一共n種，如果你集齊了這n種圖案就可以召喚神龍兌換大獎。

現在請問，在理想（平均）情況下，你買多少張彩票才能獲得大獎的？

\(n\leq33\)

分析：

本題我們設已經有了k個圖案

令

\[a=\frac{k}{n}\]

設拿到一種新的圖案需要t次。

則概率為：

\[a^{t-1}(1-a)\]

則平均需要（已提出了（1-a））:

\[(1-a)(1+2a+3a^2+4a^3+5a^4+...)\]

即為

\[E(1-a)\]

而此時我們需要觀察其和\(E(a)\)的關係：

\[E(a)=a+2a^2+3a^3+4a^4+...=E-1-a-a^2-a^3...\]

整理可得

\[E(1-a)=1+a+a^2+a^3=\frac{1}{1-a}\]

然後代換一下

\[E(1-a)=\frac{n}{n-k}\]

這樣結論就顯而易見了：

假設有k個圖案在手，那麼平均再買\(\frac{n}{n-k}\) 次就可以再得到一種新的圖案，故可得總次數為：

\[(\frac{1}{n}+\frac{1}{n-1}+\frac{1}{n-2}+\frac{1}{n-3}+\frac{1}{2}+1)n\]

但是這樣最後可能會得到一個分數，這就導致輸出變得並不是那麼方便為自己偷懶找理由

7.期望與均值？

期望與均值是兩個十分相近的概念，但又可以說是截然不同。

• 均值往往是在實驗中簡單的對資料進行平均。

• 而期望就好像在上帝視角的人。

舉個擲骰子的例子：

我們的均值怎麼算呢？

顯然要擲上一定多的次數來求平均數。

比如，擲了6次，分別為1,5,5,6,3,3，那麼均值為

\[\frac{1+5+5+6+3+3}{6}=3.8333333...\]

居然無限迴圈小數...看來我是自己出數坑自己

可是期望呢？

我們不用擲骰子就能計算出來：

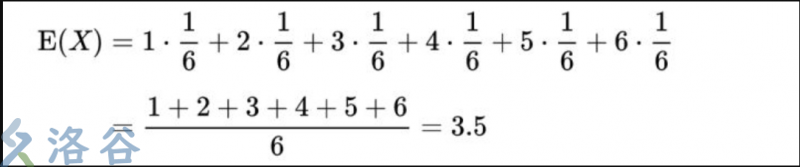
可以看出，兩個值是有明顯差別的，而且還時刻不同。

但是為什麼容易弄混呢？

因為我太弱了在將多個均值求均值後，兩者就無限接近了。

8、期望的小性質：

• 設X是隨機變數，C是常數，則\(E(CX)=C\times E(X)\)

簡單證明一下：

設x 的多個隨機變數為

\[Ca_1,Ca_2,Ca_3\]

對應的出現概率為

\[p_1,p_2,p_3\]

那麼對應的求期望的式子

\[E(CX)=C(a_1\times p_1 +a_2\times p_2 +a_3\times p_3 )\]

(C提出來)

由於：

\[E(X)=a_1\times p_1 +a_2\times p_2 +a_3\times p_3\]

所以

\[E(CX)=C\times E(X)\]

下面的可以自行思考，都不難

• 設X，Y是任意兩個隨機變數，則有\(E(X+Y)=E(X)+E(Y)\)。

• 設X，Y是相互獨立的隨機變數，則有\(E(XY)=E(X)\times E(Y)\)。

• 設C為常數，則\(E(C)=C\)。

9、期望的應用

彩票問題

在買彩票中，大多數人相信基本上是沒法中獎的，但還是有少數人幻想，於是就再這裡簡要分析一個彩票問題的期望.

設一張彩票為2元，每售\(1000000\)張開獎，假設中獎號碼為\(342356\)，則每張彩票有一個對應的六位數號碼，獎次如下：（中獎不疊加）

• 末位相等,安慰獎：獎勵4元，中獎概率0.1%

• 後兩位相等,幸運獎：獎勵20元，中獎概率0.01%

• 後三位相等,手氣獎：獎勵200元，中獎概率0.001%

• 後四位相等,一等獎：獎勵2000元，中獎概率0.0001%

• 後五位相等,特等獎：獎勵20000元，中獎概率0.00001%

某大佬：咦我六位都相等，快給我200000元！！！

彩票公司:你沒看你這一項沒有嗎？你只是特等獎（我是不會告訴你再給錢就虧了

那到底為什麼虧了呢

我們來用簡單的概率知識來計算一下，對於每一位購買彩票的使用者，公司可能支出為：

\[0.1\times 4+0.01\times 20+0.001\times 200+0.0001\times 2000+0.00001\times 20000=1.2\]

也就是說，公司期望對每個人賺0.8元。

每1000000張，就是800000元！

回到剛才大佬的疑問，顯然，如果按照開獎規律繼續的話，公司會少賺200000元！！

這顯然是一筆不小的損失

彩票公司：我這怎麼給員工發工資？！

dalao:

由此可見，彩票公司售賣彩票會讓買家有驚現不同的體驗（獎次不同），但即使是隨機生成彩票號碼，賣得多了所支出的錢一定在期望值附近，而能保證穩定的收入，而且彩票單價低，還有可能中那麼多獎，買的人多，這樣彩票市場才得以持續下去。

10、條件期望

這種期望的求解一般是在有一定條件下的。廢話

如下題：

假設你不斷扔一個等概率的六面骰子，直到扔出6停止。求在骰子只出現過偶數的條件下扔骰子次數的期望。

分析：

第一眼，我的答案是3

至於如何得出的，在這裡就不賣關子了，因為上面的答案是錯的！

思考一下，為什麼呢？

我們再讀一下題：

假設你不斷扔一個等概率的六面骰子，直到扔出6停止。求在骰子只出現過偶數的條件下扔骰子次數的期望。

求在骰子只出現過偶數的條件下扔骰子次數的期望。

只出現過偶數的條件

只出現過偶數

只出現

只

抽絲剝繭

細細的考慮一下，題目所說的並不是指出現奇數就pass再扔，而是出現奇數就終止了操作！！！

所以把條件這樣轉換後，就可以得到正確答案：\(\frac{3}{2}\) 了

什麼？你問怎麼得到的？

那我把題意轉換一下：

假設你不斷扔一個等概率的六面骰子，直到扔出1,3,5，6停止。求骰子最後一次是6次數的期望。

這樣再結合前面的知識，大家應該都明白了吧。

這類問題屬於數學期望中較有拓展的知識，考察的概率較低，感興趣者可作為興趣鑽研。其實也不難

n.後記：

期望的定義等少數內容為了精準參考了百度百科即其他大佬的blog等,本文如有錯誤，歡迎大佬指