阿里妹導讀：金鑰管理是密碼學應用的核心問題之一。任何涉及加密/簽名的應用，無論演算法本身機制多麼安全，最終都會受到靈魂拷問：你金鑰存在哪兒？本文實現了一種安全的金鑰管理方案，基於安全多方計算技術，避免了客戶端、伺服器端記憶體中的金鑰洩露風險，並已經在阿里集團內的金鑰管理系統上線。

背景介紹：金鑰管理

提問：你金鑰存在哪兒？

對這一問的回答基本可概括為2類：

a. 本地加解密：金鑰儲存在某些介質（如配置檔案、資料庫，也可以是某個遠端伺服器）中，使用者在需要進行加密/簽名時，從這些介質拉取金鑰（可能拉取的只是金鑰密文，需要再解密出金鑰明文），然後本地進行加密/簽名。

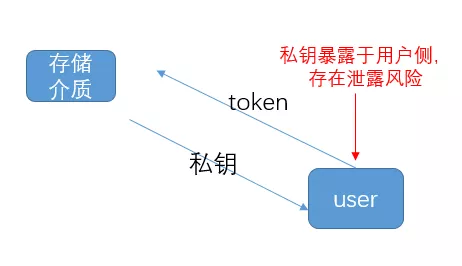
b. 伺服器加解密：

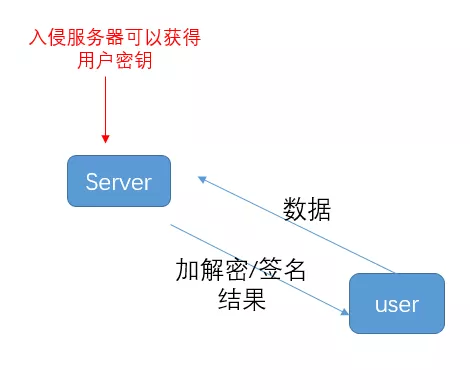
一般的金鑰管理系統都可歸到這兩類模式，但是他們都存在各自的問題：

1. 前者由於金鑰是被拉到了使用者本地，暴露在使用者記憶體中，而使用者本機的安全性是無法做任何假設的，可能存在各種漏洞/木馬等，因此金鑰面臨著各類洩露風險；在客戶端引入 TEE 可以提升這個安全門檻，但是需要配置額外的硬體，而且沒有100%杜絕洩露風險（如側通道等）；
2. 後者的金鑰是完全交給了伺服器，萬一伺服器存在漏洞/伺服器被入侵/伺服器管理員作惡，那麼使用者隱私便在伺服器面前一覽無餘。

可能有些同學覺得這2類風險不夠高，但是對於高價值資料，這些風險是不可忽視的。舉個例子，假設你是中本聰，那麼你的比特幣創世塊地址對應的私鑰放哪才能不忘掉，同時不洩露呢？是不是好像這兩種方法都無法滿足需求了？

基於安全多方計算的金鑰管理(MPC KMS)，也稱門限簽名/門限加密，即是為了解決這一對矛盾。簡而言之，MPC KMS 將使用者金鑰分為 M 份"碎片"（例如 M=2，金鑰是100，可以拆成兩份30和70），儲存在 M 個不同的伺服器中（例如一份存在A雲服務商，一份存在B雲服務商），任何一個伺服器都無法獨立根據自己的"碎片"恢復出使用者金鑰原文。當用戶需要進行加密/簽名時，則在這 M 個伺服器之間執行一個 MPC 協議，產生加密/簽名的結果，且整個過程中不需要復原使用者金鑰。

如果最少只需要 n 個伺服器參與即可完成協議，則稱之為 n of M 的門限簽名/加密。

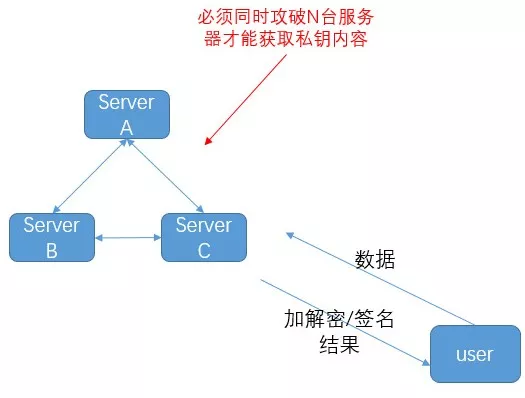
可見，在 MPC KMS 中，上述兩種風險均可以得到有效的規避：首先，使用者本地環境的安全問題不會導致金鑰洩露；其次，即使某個伺服器出問題，攻擊者也無法得到使用者的金鑰，必須同時攻陷 n 個伺服器，或是 n 個伺服器管理員一起合謀（如果我們把伺服器部署在多個獨立的雲服務系統上，這種同時出問題的概率幾乎可以忽略）。

MPC KMS 這種去中心化金鑰管理的特點和區塊鏈的共識機制具有非常好的相容性：除了直接用於保管使用者私鑰、節點金鑰之外，使用者還可以把私鑰託管分成 M 片，託管在區塊鏈的 M 個節點，然後設定僅當滿足一定門限的節點（例如1/4的節點）產生共識時才能動用他的某筆數字貨幣財產；或是設定某個軟體包的釋出必須經過一定門限的節點簽名等等。

安全多方計算 MPC 介紹

安全多方計算（ Secure Multi-Party Computation，MPC）在80年代由姚期智院士提出。安全多方計算協議允許多個數據所有者進行資料協同計算，輸出計算結果，並保證任何一方均無法得到除應得的計算結果之外的其他任何資訊。

這裡的黑色加粗字型的文字是格外需要注意的：不僅僅是無法獲取原始資料，而是無法獲得其他任何資訊。以百萬富翁問題為例：兩個百萬富翁比誰的錢數更多，最後雙方獲得的唯一資訊只能是“大於、等於或小於”；只要洩露了任何的其他額外資訊（譬如對方錢數的最高位是1還是2），無論這個額外資訊多麼少，都不能算 MPC。

MPC 還有很多潛在應用場景，如基於融合資料的聯合風控、聯合廣告推薦等，它能夠真正實現“資料可用不可見”，在這個資料為王的時代有著美妙的前景。

安全多方計算+金鑰管理MPC KMS介紹

技術架構

MPC KMS 即是安全多方計算 MPC 的一種特殊場景：各方分別持有金鑰的一部分，協同計算的目的是加解密/簽名，同時除了加解密/簽名結果之外，不洩露任何其他資訊。

我們研讀了多篇最新論文[1,2,3]，在這些論文的理論基礎之上，實現了安全兩方 ECDSA 簽名系統。系統的粗粒度互動過程如下，詳細演算法可以參閱論文。

1.金鑰生成：使用者發起生成請求，兩臺伺服器 A 和 B 分別各自獨立的產生隨機數 a 和隨機數 b，a+b 即是簽名時使用的私鑰。

2.簽名：使用者首先從 A 伺服器拉取 a，然後呼叫 B 的服務，把需要簽名的訊息message 和 message、a 的加密計算結果傳送給 B，和 B 之間執行一個安全兩方簽名協議，得到最終的簽名值。在整個過程中，私鑰a+b沒有在任何一方的記憶體中復原，任何一方都無法瞭解到私鑰 a+b 的內容。

操作流程

最終系統暴露給使用者的是兩個介面 getPK() 和 sign()，介面以阿里內部常用的HSF(High-speed Service Framework) 方式提供，接入非常方便。

Step 1. 使用者首先在金鑰管理伺服器上新建一個金鑰，後臺的兩臺伺服器會自動的產生各自的金鑰分量；

Step 2.使用者呼叫 getPK() 獲取該金鑰對應的公鑰；

Step 3.使用者在金鑰管理伺服器上新建一個 SHA256WithECDSA 型別的公鑰，選擇手工輸入，輸入 Step 2得到的內容；

Step 4.使用者此後就可以通過 sign() 來呼叫安全兩方簽名，通過金鑰管理伺服器提供的ECDSA verifier 函式，輸入公鑰來驗證簽名的正確性了。

Step 5. 這下安全性超有保障，連管理員都得兩個伺服器的管理員一起碼程式碼才能知道你的私鑰到底是啥了！

關於我們

阿里安全雙子座實驗室 - 密態計算技術團隊，專精於安全多方計算、同態加密等高階應用密碼學技術，研發的產品“盲劍客”已被用於保護阿里經濟體內外億級使用者的資料安全。若有需求，歡迎垂詢@鴻程。

參考文獻：

[1] Lindell Y. Fast secure two-party ECDSA signing[C]//Annual International Cryptology Conference (CRYPTO). Springer, Cham, 2017: 613-644.
[2] Doerner J, Kondi Y, Lee E, et al. Secure Two-party Threshold ECDSA from ECDSA Assumptions[C]//2018 IEEE Symposium on Security and Privacy (SP). IEEE, 2018: 980-997.
[3] Lindell Y, Nof A. Fast secure multiparty ecdsa with practical distributed key generation and applications to cryptocurrency custody[C]//Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security (CCS). ACM, 2018: 1837-1854.

作者：鴻程

原文連結​

本文為雲棲社群原創內容，未經