JavaScript 資料結構與演算法之美 - 桶排序、計數排序、基數排序

1. 前言
演算法為王。
想學好前端,先練好內功,只有內功深厚者,前端之路才會走得更遠。
筆者寫的 JavaScript 資料結構與演算法之美 系列用的語言是 JavaScript ,旨在入門資料結構與演算法和方便以後複習。
之所以把 計數排序、桶排序、基數排序 放在一起比較,是因為它們的平均時間複雜度都為 O(n)。
因為這三個排序演算法的時間複雜度是線性的,所以我們把這類排序演算法叫作 線性排序(Linear sort)。
之所以能做到線性的時間複雜度,主要原因是,這三個演算法不是基於比較的排序演算法,都不涉及元素之間的比較操作。
另外,請大家帶著問題來閱讀下文,問題:如何根據年齡給 100 萬用戶排序 ?
2. 桶排序(Bucket Sort)
桶排序是計數排序的升級版,也採用了分治思想。
思想
- 將要排序的資料分到有限數量的幾個有序的桶裡。
- 每個桶裡的資料再單獨進行排序(一般用插入排序或者快速排序)。
- 桶內排完序之後,再把每個桶裡的資料按照順序依次取出,組成的序列就是有序的了。
比如:

桶排序利用了函式的對映關係,高效與否的關鍵就在於這個對映函式的確定。
為了使桶排序更加高效,我們需要做到這兩點:
- 在額外空間充足的情況下,儘量增大桶的數量。
- 使用的對映函式能夠將輸入的 N 個數據均勻的分配到 K 個桶中。
桶排序的核心:就在於怎麼把元素平均分配到每個桶裡,合理的分配將大大提高排序的效率。
實現
// 桶排序 const bucketSort = (array, bucketSize) => { if (array.length === 0) { return array; } console.time('桶排序耗時'); let i = 0; let minValue = array[0]; let maxValue = array[0]; for (i = 1; i < array.length; i++) { if (array[i] < minValue) { minValue = array[i]; //輸入資料的最小值 } else if (array[i] > maxValue) { maxValue = array[i]; //輸入資料的最大值 } } //桶的初始化 const DEFAULT_BUCKET_SIZE = 5; //設定桶的預設數量為 5 bucketSize = bucketSize || DEFAULT_BUCKET_SIZE; const bucketCount = Math.floor((maxValue - minValue) / bucketSize) + 1; const buckets = new Array(bucketCount); for (i = 0; i < buckets.length; i++) { buckets[i] = []; } //利用對映函式將資料分配到各個桶中 for (i = 0; i < array.length; i++) { buckets[Math.floor((array[i] - minValue) / bucketSize)].push(array[i]); } array.length = 0; for (i = 0; i < buckets.length; i++) { quickSort(buckets[i]); //對每個桶進行排序,這裡使用了快速排序 for (var j = 0; j < buckets[i].length; j++) { array.push(buckets[i][j]); } } console.timeEnd('桶排序耗時'); return array; }; // 快速排序 const quickSort = (arr, left, right) => { let len = arr.length, partitionIndex; left = typeof left != 'number' ? 0 : left; right = typeof right != 'number' ? len - 1 : right; if (left < right) { partitionIndex = partition(arr, left, right); quickSort(arr, left, partitionIndex - 1); quickSort(arr, partitionIndex + 1, right); } return arr; }; const partition = (arr, left, right) => { //分割槽操作 let pivot = left, //設定基準值(pivot) index = pivot + 1; for (let i = index; i <= right; i++) { if (arr[i] < arr[pivot]) { swap(arr, i, index); index++; } } swap(arr, pivot, index - 1); return index - 1; }; const swap = (arr, i, j) => { let temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; };
測試
const array = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
console.log('原始array:', array);
const newArr = bucketSort(array);
console.log('newArr:', newArr);
// 原始 array: [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
// 堆排序耗時: 0.133056640625ms
// newArr: [1, 2, 2, 3, 4, 5, 5, 6, 8, 9]分析
- 第一,桶排序是原地排序演算法嗎 ?
因為桶排序的空間複雜度,也即記憶體消耗為 O(n),所以不是原地排序演算法。
- 第二,桶排序是穩定的排序演算法嗎 ?
取決於每個桶的排序方式,比如:快排就不穩定,歸併就穩定。
- 第三,桶排序的時間複雜度是多少 ?
因為桶內部的排序可以有多種方法,是會對桶排序的時間複雜度產生很重大的影響。所以,桶排序的時間複雜度可以是多種情況的。
總的來說
最佳情況:當輸入的資料可以均勻的分配到每一個桶中。
最差情況:當輸入的資料被分配到了同一個桶中。
以下是桶的內部排序為快速排序的情況:
如果要排序的資料有 n 個,我們把它們均勻地劃分到 m 個桶內,每個桶裡就有 k =n / m 個元素。每個桶內部使用快速排序,時間複雜度為 O(k * logk)。
m 個桶排序的時間複雜度就是 O(m * k * logk),因為 k = n / m,所以整個桶排序的時間複雜度就是 O(n*log(n/m))。
當桶的個數 m 接近資料個數 n 時,log(n/m) 就是一個非常小的常量,這個時候桶排序的時間複雜度接近 O(n)。
最佳情況:T(n) = O(n)。當輸入的資料可以均勻的分配到每一個桶中。
最差情況:T(n) = O(nlogn)。當輸入的資料被分配到了同一個桶中。
平均情況:T(n) = O(n)。
桶排序最好情況下使用線性時間 O(n),桶排序的時間複雜度,取決與對各個桶之間資料進行排序的時間複雜度,因為其它部分的時間複雜度都為 O(n)。
很顯然,桶劃分的越小,各個桶之間的資料越少,排序所用的時間也會越少。但相應的空間消耗就會增大。
適用場景
- 桶排序比較適合用在外部排序中。
- 外部排序就是資料儲存在外部磁碟且資料量大,但記憶體有限,無法將整個資料全部載入到記憶體中。
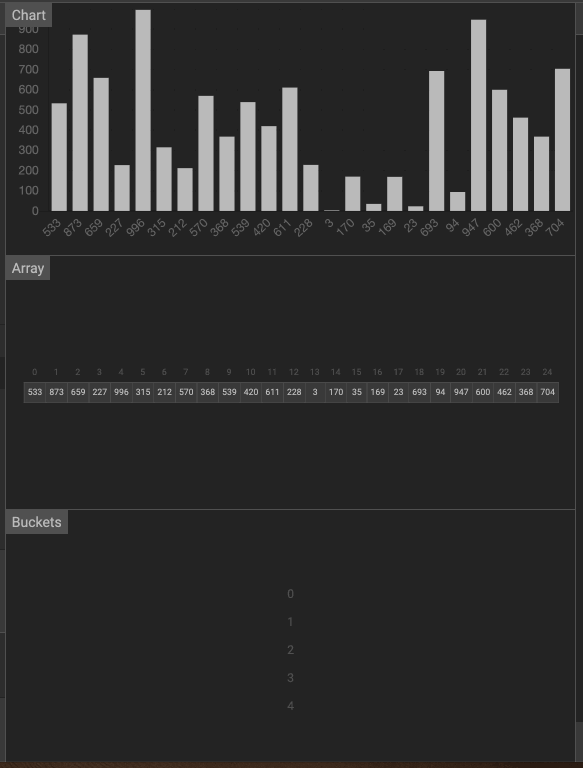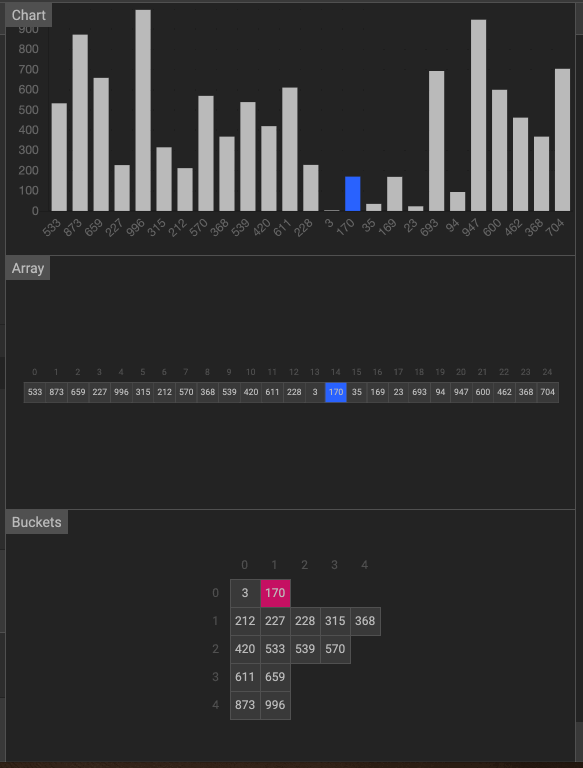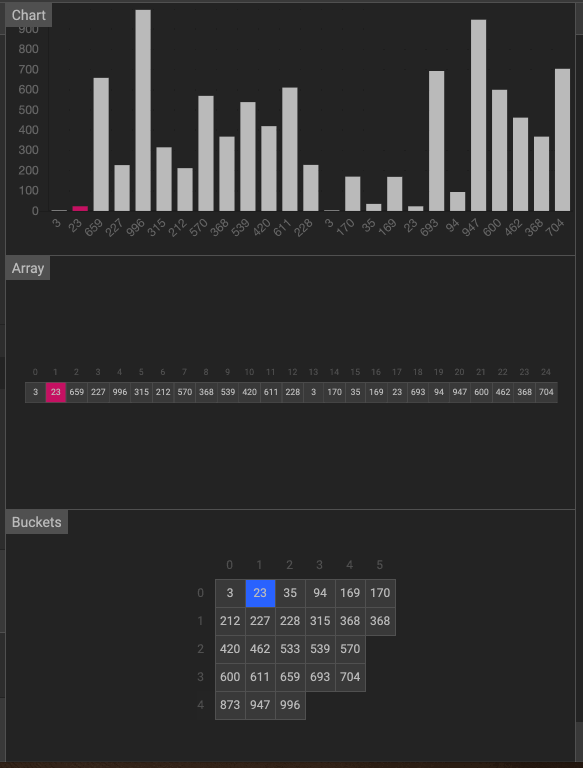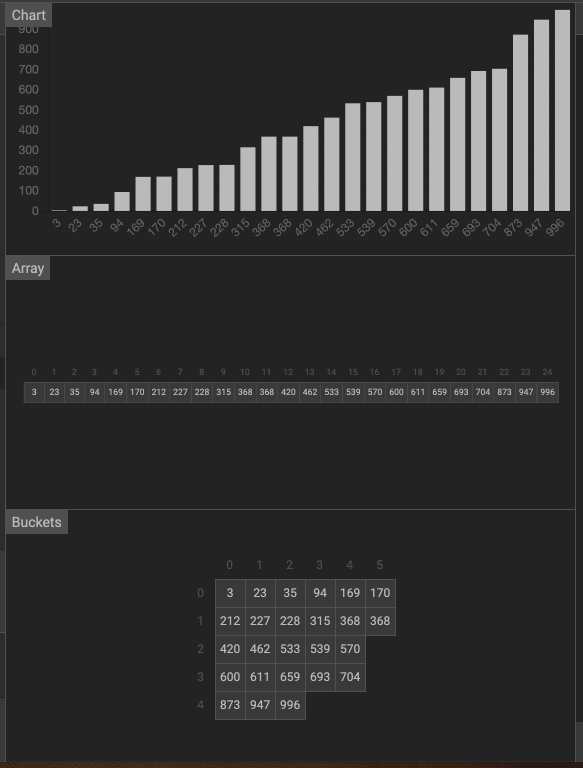
動畫
3. 計數排序(Counting Sort)
思想
- 找出待排序的陣列中最大和最小的元素。
- 統計陣列中每個值為 i 的元素出現的次數,存入新陣列 countArr 的第 i 項。
- 對所有的計數累加(從 countArr 中的第一個元素開始,每一項和前一項相加)。
- 反向填充目標陣列:將每個元素 i 放在新陣列的第 countArr[i] 項,每放一個元素就將 countArr[i] 減去 1 。
關鍵在於理解最後反向填充時的操作。
使用條件
- 只能用在資料範圍不大的場景中,若資料範圍 k 比要排序的資料 n 大很多,就不適合用計數排序。
- 計數排序只能給非負整數排序,其他型別需要在不改變相對大小情況下,轉換為非負整數。
- 比如如果考試成績精確到小數後一位,就需要將所有分數乘以 10,轉換為整數。
實現
方法一:
const countingSort = array => {
let len = array.length,
result = [],
countArr = [],
min = (max = array[0]);
console.time('計數排序耗時');
for (let i = 0; i < len; i++) {
// 獲取最小,最大 值
min = min <= array[i] ? min : array[i];
max = max >= array[i] ? max : array[i];
countArr[array[i]] = countArr[array[i]] ? countArr[array[i]] + 1 : 1;
}
console.log('countArr :', countArr);
// 從最小值 -> 最大值,將計數逐項相加
for (let j = min; j < max; j++) {
countArr[j + 1] = (countArr[j + 1] || 0) + (countArr[j] || 0);
}
console.log('countArr 2:', countArr);
// countArr 中,下標為 array 數值,資料為 array 數值出現次數;反向填充資料進入 result 資料
for (let k = len - 1; k >= 0; k--) {
// result[位置] = array 資料
result[countArr[array[k]] - 1] = array[k];
// 減少 countArr 陣列中儲存的計數
countArr[array[k]]--;
// console.log("array[k]:", array[k], 'countArr[array[k]] :', countArr[array[k]],)
console.log('result:', result);
}
console.timeEnd('計數排序耗時');
return result;
};測試
const array = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
console.log('原始 array: ', array);
const newArr = countingSort(array);
console.log('newArr: ', newArr);
// 原始 array: [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2]
// 計數排序耗時: 5.6708984375ms
// newArr: [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]
方法二:
const countingSort2 = (arr, maxValue) => {
console.time('計數排序耗時');
maxValue = maxValue || arr.length;
let bucket = new Array(maxValue + 1),
sortedIndex = 0;
(arrLen = arr.length), (bucketLen = maxValue + 1);
for (let i = 0; i < arrLen; i++) {
if (!bucket[arr[i]]) {
bucket[arr[i]] = 0;
}
bucket[arr[i]]++;
}
for (let j = 0; j < bucketLen; j++) {
while (bucket[j] > 0) {
arr[sortedIndex++] = j;
bucket[j]--;
}
}
console.timeEnd('計數排序耗時');
return arr;
};測試
const array2 = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
console.log('原始 array2: ', array2);
const newArr2 = countingSort2(array2, 21);
console.log('newArr2: ', newArr2);
// 原始 array: [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2]
// 計數排序耗時: 0.043212890625ms
// newArr: [1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]例子
可以認為,計數排序其實是桶排序的一種特殊情況。
當要排序的 n 個數據,所處的範圍並不大的時候,比如最大值是 k,我們就可以把資料劃分成 k 個桶。每個桶內的資料值都是相同的,省掉了桶內排序的時間。
我們都經歷過高考,高考查分數系統你還記得嗎?我們查分數的時候,系統會顯示我們的成績以及所在省的排名。如果你所在的省有 50 萬考生,如何通過成績快速排序得出名次呢?
- 考生的滿分是 900 分,最小是 0 分,這個資料的範圍很小,所以我們可以分成 901 個桶,對應分數從 0 分到 900 分。
- 根據考生的成績,我們將這 50 萬考生劃分到這 901 個桶裡。桶內的資料都是分數相同的考生,所以並不需要再進行排序。
- 我們只需要依次掃描每個桶,將桶內的考生依次輸出到一個數組中,就實現了 50 萬考生的排序。
- 因為只涉及掃描遍歷操作,所以時間複雜度是 O(n)。
分析
- 第一,計數排序是原地排序演算法嗎 ?
因為計數排序的空間複雜度為 O(k),k 是桶的個數,所以不是原地排序演算法。 - 第二,計數排序是穩定的排序演算法嗎 ?
計數排序不改變相同元素之間原本相對的順序,因此它是穩定的排序演算法。 - 第三,計數排序的時間複雜度是多少 ?
最佳情況:T(n) = O(n + k)
最差情況:T(n) = O(n + k)
平均情況:T(n) = O(k)
k:桶的個數。
動畫
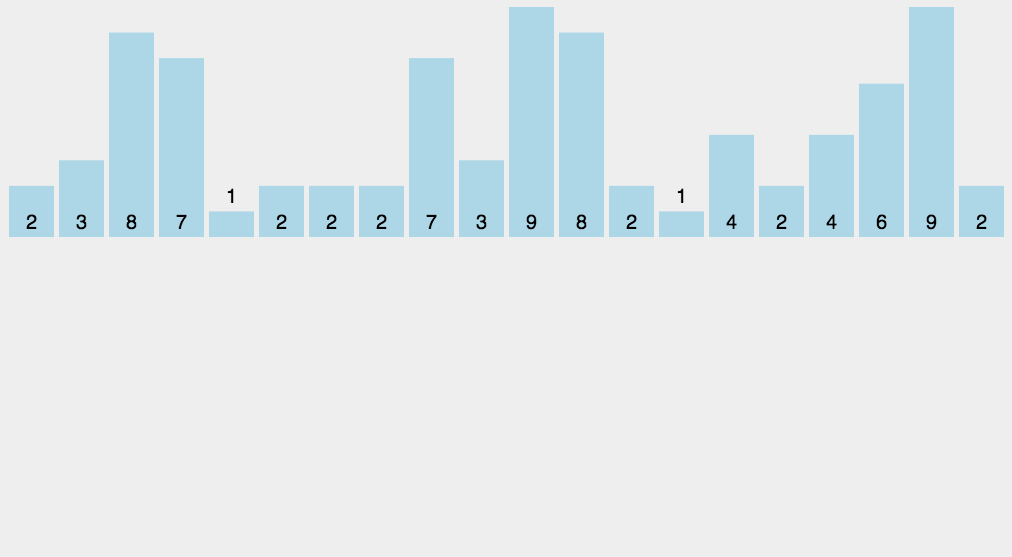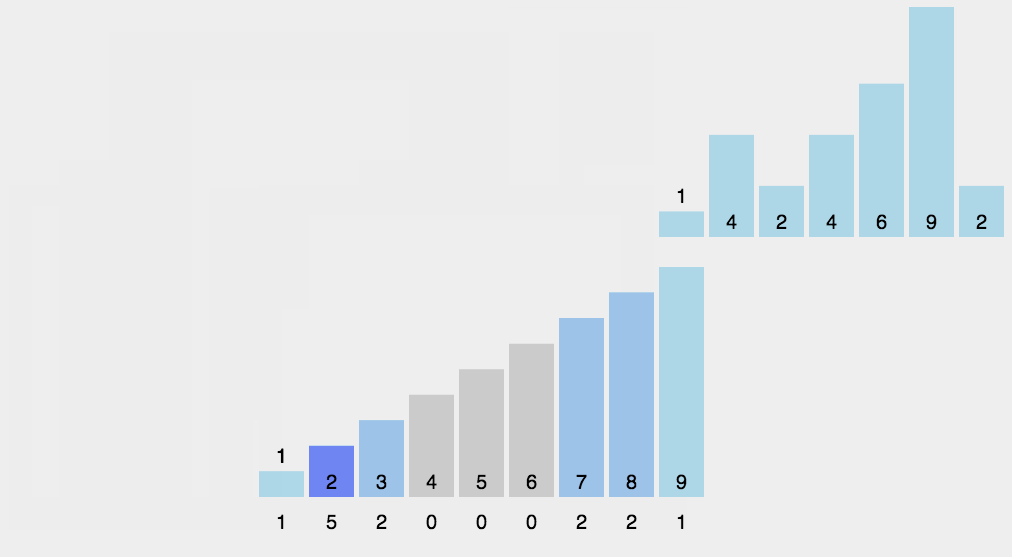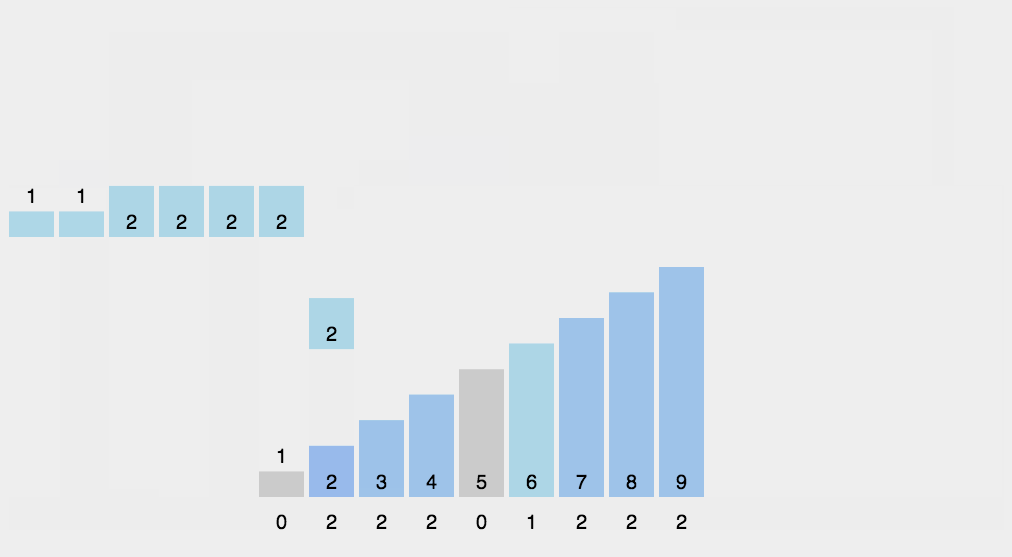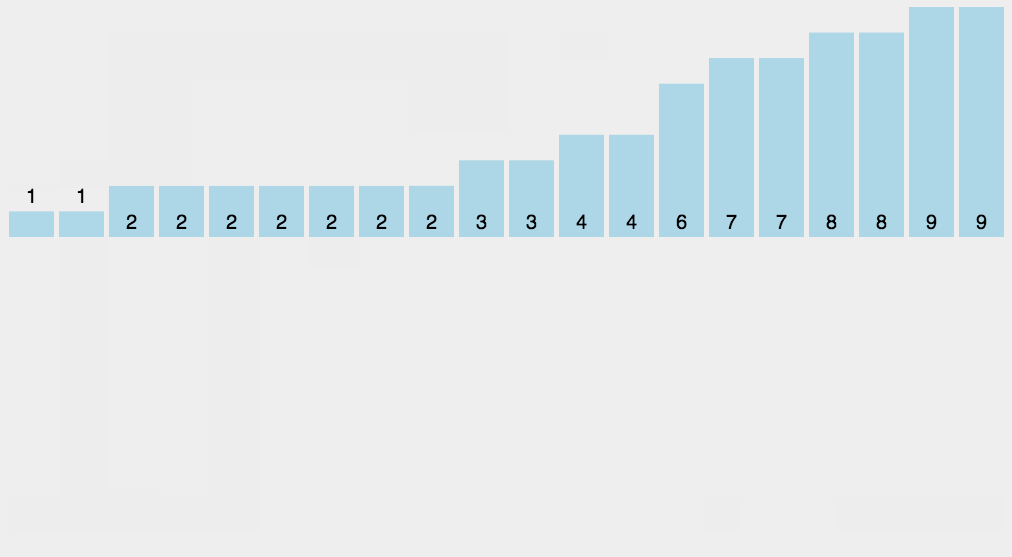
4. 基數排序(Radix Sort)
思想
基數排序是一種非比較型整數排序演算法,其原理是將整數按位數切割成不同的數字,然後按每個位數分別比較。
由於整數也可以表達字串(比如名字或日期)和特定格式的浮點數,所以基數排序也不是隻能使用於整數。
例子
假設我們有 10 萬個手機號碼,希望將這 10 萬個手機號碼從小到大排序,你有什麼比較快速的排序方法呢 ?
這個問題裡有這樣的規律:假設要比較兩個手機號碼 a,b 的大小,如果在前面幾位中,a 手機號碼已經比 b 手機號碼大了,那後面的幾位就不用看了。所以是基於位來比較的。
桶排序、計數排序能派上用場嗎 ?手機號碼有 11 位,範圍太大,顯然不適合用這兩種排序演算法。針對這個排序問題,有沒有時間複雜度是 O(n) 的演算法呢 ? 有,就是基數排序。
使用條件
- 要求資料可以分割獨立的
位來比較; - 位之間由遞進關係,如果 a 資料的高位比 b 資料大,那麼剩下的地位就不用比較了;
- 每一位的資料範圍不能太大,要可以用線性排序,否則基數排序的時間複雜度無法做到 O(n)。
方案
按照優先從高位或低位來排序有兩種實現方案:
- MSD:由高位為基底,先按 k1 排序分組,同一組中記錄, 關鍵碼 k1 相等,再對各組按 k2 排序分成子組, 之後,對後面的關鍵碼繼續這樣的排序分組,直到按最次位關鍵碼 kd 對各子組排序後,再將各組連線起來,便得到一個有序序列。MSD 方式適用於位數多的序列。
- LSD:由低位為基底,先從 kd 開始排序,再對 kd - 1 進行排序,依次重複,直到對 k1 排序後便得到一個有序序列。LSD 方式適用於位數少的序列。
實現
/**
* name: 基數排序
* @param array 待排序陣列
* @param max 最大位數
*/
const radixSort = (array, max) => {
console.time('計數排序耗時');
const buckets = [];
let unit = 10,
base = 1;
for (let i = 0; i < max; i++, base *= 10, unit *= 10) {
for (let j = 0; j < array.length; j++) {
let index = ~~((array[j] % unit) / base); //依次過濾出個位,十位等等數字
if (buckets[index] == null) {
buckets[index] = []; //初始化桶
}
buckets[index].push(array[j]); //往不同桶裡新增資料
}
let pos = 0,
value;
for (let j = 0, length = buckets.length; j < length; j++) {
if (buckets[j] != null) {
while ((value = buckets[j].shift()) != null) {
array[pos++] = value; //將不同桶裡資料挨個撈出來,為下一輪高位排序做準備,由於靠近桶底的元素排名靠前,因此從桶底先撈
}
}
}
}
console.timeEnd('計數排序耗時');
return array;
};測試
const array = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log('原始array:', array);
const newArr = radixSort(array, 2);
console.log('newArr:', newArr);
// 原始 array: [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48]
// 堆排序耗時: 0.064208984375ms
// newArr: [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]分析
第一,基數排序是原地排序演算法嗎 ?
因為計數排序的空間複雜度為 O(n + k),所以不是原地排序演算法。第二,基數排序是穩定的排序演算法嗎 ?
基數排序不改變相同元素之間的相對順序,因此它是穩定的排序演算法。第三,基數排序的時間複雜度是多少 ?
最佳情況:T(n) = O(n * k)
最差情況:T(n) = O(n * k)
平均情況:T(n) = O(n * k)
k 是待排序列最大值。
動畫
LSD 基數排序動圖演示:

5. 解答開篇
回過頭來看看開篇的思考題:如何根據年齡給 100 萬用戶排序 ?
你可能會說,我用上一節講的歸併、快排就可以搞定啊!是的,它們也可以完成功能,但是時間複雜度最低也是 O(nlogn)。
有沒有更快的排序方法呢 ?以下是參考答案。
- 實際上,根據年齡給 100 萬用戶排序,就類似按照成績給 50 萬考生排序。
- 我們假設年齡的範圍最小 1 歲,最大不超過 120 歲。
- 我們可以遍歷這 100 萬用戶,根據年齡將其劃分到這 120 個桶裡,然後依次順序遍歷這 120 個桶中的元素。
- 這樣就得到了按照年齡排序的 100 萬用戶資料。
6. 複雜性對比
基數排序 vs 計數排序 vs 桶排序
基數排序有兩種方法:
- MSD 從高位開始進行排序
- LSD 從低位開始進行排序
這三種排序演算法都利用了桶的概念,但對桶的使用方法上有明顯差異:
- 基數排序:根據鍵值的每位數字來分配桶;
- 計數排序:每個桶只儲存單一鍵值;
- 桶排序:每個桶儲存一定範圍的數值;
複雜性對比
| 名稱 | 平均 | 最好 | 最壞 | 空間 | 穩定性 | 排序方式 |
|---|---|---|---|---|---|---|
| 桶排序 | O(n + k) | O(n + k) | O(n2) | O(n + k) | Yes | Out-place |
| 計數排序 | O(n + k) | O(n + k) | O(n + k) | O(k) | Yes | Out-place |
| 基數排序 | O(n * k) | O(n * k) | O(n * k) | O(n + k) | Yes | Out-place |
n: 資料規模
桶排序的時間複雜度可以是多種情況的,取決於桶內的排序。
7. 最後
文中所有的程式碼及測試事例都已經放到我的 GitHub 上了。
覺得有用 ?喜歡就收藏,順便點個贊吧,你的支援是我最大的鼓勵!
參考文章:
- 菜鳥教程 - 算法系列
- 線性排序:如何根據年齡給100萬用戶資料排序?
- 十大經典排序演算法總結(JavaScript 描述)
- JS 中可能用得到的全部的排序演算法
