tensorflow學習筆記——自編碼器及多層感知器
1，自編碼器簡介
傳統機器學習任務很大程度上依賴於好的特徵工程，比如對數值型，日期時間型，種類型等特徵的提取。特徵工程往往是非常耗時耗力的，在影象，語音和視訊中提取到有效的特徵就更難了，工程師必須在這些領域有非常深入的理解，並且使用專業演算法提取這些資料的特徵。深度學習則可以解決人工難以提取有效特徵的問題，它可以大大緩解機器學習模型對特徵工程的依賴。深度學習在早期一度被認為是一種無監督的特徵學習（Unsuperbised Feature Learning），模仿了人腦的對特徵逐層抽象提取的過程。這其中有兩點很重要：一是無監督學習，即我們不需要標註資料就可以對資料進行一定程度的學習，這種學習是對資料內容的組織形式的學習，提取的時頻繁出現的特徵；二是逐層抽象，特徵是需要不斷抽象的，就像人總是從簡單基礎的概念開始學習，再到複雜的概念。學生們要從加減乘除開始學起，再到簡單函式，然後到微積分，深度學習也是一樣的，它從簡單的微觀的特徵開始，不斷抽象特徵的層級，逐漸往復雜的巨集觀特徵轉變。
例如在影象識別問題中，假定我們有許多汽車的圖片，要如何判定這些圖片是汽車呢？如果我們從畫素級特徵開始進行訓練分類器，那麼絕大多數演算法很難有效的工作。如果我們提取出高階的特徵，比如汽車的車輪，汽車的車窗，汽車的車身，那麼使用這些高階特徵便可以非常準確地對圖片進行分類，這就是高階特徵的效果。不過任何高階特徵都是由更小單位的特徵組合而成的。比如車輪是由橡膠輪胎，車軸，輪輻等組成。而其中每一個元件都是由更小單位的特徵組合而成的，比如橡膠輪胎由許多黑色的同心圓組成的，而這些同心圓也都由許多圓弧曲線組成，圓弧曲線都由畫素組成。我們將漆面的過程逆過來，將一張圖片的原始畫素慢慢抽象，從畫素組成點，線，再講點，線組合成小零件，再將小零件組成車輪，車窗，車身等高階特徵，這邊是深度學習在訓練過程中所作的特徵學習。
早年由學者們研究稀疏編碼（Sparse Coding）時，他們收集了大量黑白風景照，並從中提取了許多16畫素*16畫素的影象碎片。他們發現幾乎所有的影象碎片都可以由64種正交的邊組合得到，如下圖所示，並且組合出一張影象碎片需要的邊的數量是很少的，即稀疏的。學者同時發現聲音也存在這種情況，他們從大量的未標註音訊中發現了20種基本結構，絕大多數聲音可以由這些基本結構線性組合得到。這其實就是特徵的稀疏表達，使用少量的基本特徵組合拼裝得到更高層抽象的特徵，通常我們也需要多層的神經網路，對每一層神經網路來說，前一層的輸出都是未加工的畫素，而這一層則是物件素進行加工組織成更高階的特徵（即前面提到的將邊組合成影象碎片）。
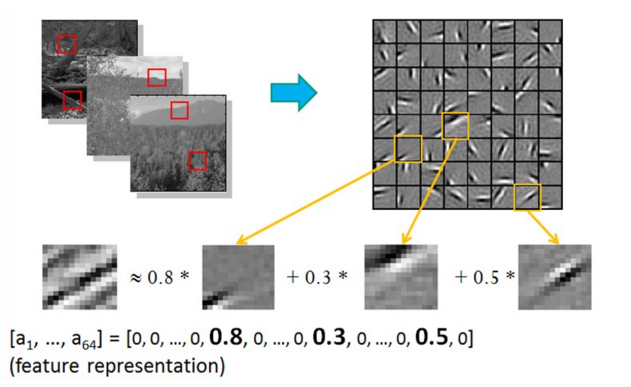
我們來看一下實際的例子。假如我們有許多基本結構，比如指向各個方向的邊，白塊，黑塊等。如下圖所示，我們可以通過不同方式組合出不同的高階特徵，並最終拼出不同的目標物體。這些基本結構就是basis，在人臉識別任務中，我們可以使用他們拼出人臉的不同器官，比如鼻子，嘴，眼睛，眉毛，臉頰等，這些器官又可以向上一層拼出不同樣式的人臉，最後模型通過在圖片中匹配這些不同樣式 的人臉（即高階特徵）來進行識別。同樣，basis可以拼出汽車上不同的元件，最終拼出各式各樣的車型；也可以拼出大象身體的不同部位，最後組成各種尺寸，品種，顏色的大象；還可以拼出椅子的凳，座，靠背凳，最後組成各種尺寸，品種，顏色的大象；還可以拼出椅子的凳，座，靠背凳，最後組成不同款式的椅子，特徵是可以不斷抽象轉為高一級的特徵的，那我們如何找到這些基本結構，然後如何抽象呢？如果我們有很多標註的資料，則可以訓練一個深層的神經網路。如果沒有標註的資料呢？在這種情況下，我們依然可以使用無監督的自編碼器來提取特徵。自編碼器（AutoEncoder），顧名思義，即可以使用自身的高階特徵編碼自己。自編碼器其實也是一種神經網路，它的輸入和輸出是一致的，它藉助稀疏編碼的思想，目標是使用稀疏的一些高階特徵重新組合來重構自己。因此，它的特點非常明顯：第一，期望輸入/輸出一致；第二，希望使用高階特徵來重構自己，而不是複製畫素點。
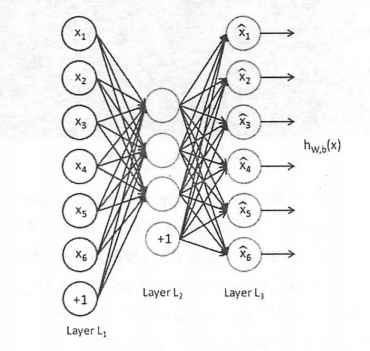
Hinton 教授在Science發表文章 Reducing the dimensionality of data with neural networks，講解了使用自編碼器對資料進行降維的方法。Hinton還提出了基於深度信念網路（Deep Belief Networks， DBN，由多層RBM堆疊而成）可使用無監督的逐層訓練的貪心演算法，為訓練很深的網路提供一個可行方案：我們可能很難直接訓練極深的網路，但是可以用無監督的逐層訓練提取特徵，將網路的權重初始化到一個比較好的位置，輔助後面的監督訓練。無監督的逐層訓練，其思想和自編碼器（AutoEncoder）非常相似，後者的目標是讓神經網路的輸出能和原始輸入一致，相當於學習一個恆等式 y=x， 如下圖所示，自編碼器的輸入節點和輸出節點的數量是一致的，但如果只是單純的逐個複製輸入節點則沒有意義，像前面提到的，自編碼器通常希望使用少量稀疏的高階特徵來重構輸入，所以我們可以加入幾種限制。
（1）如果限制中間隱含層節點的數量，比如讓中間隱含層節點的數量小於輸入/輸出節點的數量，就相當於一個降維的過程。此時已經不可能出現複製所有節點的情況，因為中間節點數小於輸入節點數，那隻能學習資料中最重要的特徵復原，將可能不太相關的內容去掉。此時，如果再給中間隱含層的權重加一個L1的正則，則可以根據懲罰係數控制隱含節點的稀疏程度，懲罰係數越大，學到的特徵組合越稀疏，實際使用（非零權重）的特徵數量越少。
（2）如果給資料加入噪音，那麼就是Denoising AutoEncoder（去噪自編碼器），我們將從噪聲中學習出資料的特徵。同樣，我們也不可能完全複製節點，完全複製並不能去除我們新增的噪聲，無法完全復原資料，所以唯有學習資料頻繁出現的模式和結構，將無規律的噪聲略去，才可以復原資料。
去噪自編碼器中最常使用的噪聲是加性高斯噪聲，其結構如下，當然也可以使用Masking Noise，即有隨機遮擋的噪聲，這種情況下，影象中的一部分畫素被置為0，模型需要從其他畫素的結構推測出這些被遮擋的畫素是什麼，因此模型依然需要學習影象中抽象的高階特徵。
如果自編碼器的隱含層只有一層，那麼其原理類似於主成分分析（PCA）。Hinton提出的DBN模型有多個隱含層，每個隱含層都是限制性玻爾茲曼機RBM（Restricted Boltzman Machine，一種具有特殊連線分佈的神經網路）。DBN訓練時，需要先對每兩層間進行無監督的預訓練（per-training），這個過程其實就相當於一個多層的自編碼器，可以將整個網路的權重初始化到一個理想的分佈。最後，通過反向傳播演算法調整模型權重，這個步驟會使用經過標註的資訊來做監督性的分類訓練。當年DBN 給訓練深層的神經網路提供了可能性，它能解決網路過深帶來的梯度瀰漫（Gradient Vanishment）的問題，讓訓練變得容易。簡單來說，Hinton的思路就是先用自編碼器的方法進行無監督的預訓練，提取特徵並初始化權重，然後使用標註資訊進行監督式的訓練。當然自編碼器的作用不僅侷限於給監督訓練做預訓練，直接使用自編碼器進行特徵提取和分析也是可以的。現實中資料最多的還是未標註的資料，因此自編碼器擁有許多用武之地。
2，TensorFlow實現自編碼器
下面我們開始實現最具代表性的去噪自編碼器。去噪自編碼器的使用範圍最廣也最通用。而其他幾種自編碼器，大家可以自己對程式碼加以修改自行實現，其中無噪聲的自編碼器只需要去掉噪聲，並保證隱含層節點小於輸入層節點；Masking Noise 的自編碼器只需要將高斯噪聲改為隨機遮擋噪聲；Variational AutoEncoder（VAE）則相對複雜，VAE則相對複雜，VAE對中間節點的分佈有強假設，擁有額外的損失項，且會使用特殊的SGVB（Stochastic Gradient Variational Bayes）演算法進行訓練。目前VAE還在生成模型中發揮了很大的作用。
這裡我們主要來自TensorFlow的開源實現，使用的資料為MNIST資料。我們的自編碼器會使用到一種引數初始化方法 xavier initialization，需要先定義好它。Xavier初始化器在Caffe的早期版本中被頻繁使用，它的特點是會根據某一層網路的輸入，輸出節點數量自動調整最適合的分佈。Xaiver Glorot 和深度學習三巨頭之一的 Yoshua Bengio 在一篇論文中指出，如果深度學習模型的權重初始化的太小，那訊號將在每層間傳遞時逐漸縮小而難以產生作用，但如果權重初始化的太大，那訊號將在每層間傳遞時逐漸放大並導致發散和實效。而 Xavier 初始化器做的事情就是讓權重被初始化的不大不小，正好合適。從數學的角度分析， Xavier 初始化器做的事情就是讓權重被初始化的不大不小，正好合適。從數學的角度分析， Xavier 初始化器就是讓權重滿足0均值，同時方差為 2/(Nin + Nout)，分佈可以用均勻分佈或者高斯分佈。如下程式碼：
def xavier_init(fan_in, fan_out, constant = 1):
low = -constant * np.sqrt(6.0 / (fan_in + fan_out))
high = constant * np.sqrt(6.0 / (fan_in + fan_out))
return tf.random_uniform((fan_in, fan_out),
minval=low, maxval=high,
dtype=tf.float32)
其中 fan_in 是輸入節點的數量，fan_out 是輸出節點的數量。我們使用了 tf.random_uniform建立了一個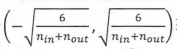
範圍內的均勻分佈，而它的方差根據公式 D(x) = (max - min) **2 /12剛好等於 2/(Nin + Nout)。因此這時實現的就是標準的均勻分佈的 Xaiver 初始化器。
程式碼如下：
#_*_coding:utf-8_*_
import numpy as np
import sklearn.preprocessing as prep
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
def xavier_init(fan_in, fan_out, constant = 1):
low = -constant * np.sqrt(6.0 / (fan_in + fan_out))
high = constant * np.sqrt(6.0 / (fan_in + fan_out))
return tf.random_uniform((fan_in, fan_out),
minval=low, maxval=high,
dtype=tf.float32)
class AdditiveGaussianNoiseAutoencoder(object):
def __init__(self, n_input, n_hidden, transfer_function=tf.nn.softplus,
optimizer=tf.train.AdamOptimizer(), scale=0.1):
self.n_input = n_input # 輸入變數數
self.n_hidden = n_hidden # 隱含層節點數
self.transfer = transfer_function # 隱含層啟用函式
self.scale = tf.placeholder(tf.float32) #高斯噪聲稀疏
self.training_scale = scale
network_weights = self._initialize_weights() # 我們只用了一個隱含層
self.weights = network_weights
self.x = tf.placeholder(tf.float32, [None, self.n_input])
self.hidden = self.transfer(tf.add(tf.matmul(
self.x + scale * tf.random_normal((n_input, )),
self.weights['w1']), self.weights['b1']
))
self.reconstruction = tf.add(tf.matmul(self.hidden,
self.weights['w2']),
self.weights['b2'])
self.cost = 0.5 * tf.reduce_sum(tf.pow(tf.subtract(
self.reconstruction, self.x), 2.0
))
self.optimizer = optimizer.minimize(self.cost)
init = tf.global_variables_initializer()
self.sess = tf.Session()
self.sess.run(init)
def _initialize_weights(self):
all_weights = dict()
all_weights['w1'] = tf.Variable(xavier_init(self.n_input, self.n_hidden))
all_weights['b1'] = tf.Variable(tf.zeros([self.n_hidden], dtype=tf.float32))
all_weights['w2'] = tf.Variable(tf.zeros([self.n_hidden,
self.n_input], dtype=tf.float32))
all_weights['b2'] = tf.Variable(tf.zeros([self.n_input], dtype=tf.float32))
return all_weights
# 計算損失cost及執行一步訓練的函式partial_fit
def partial_fit(self, X):
cost, opt = self.sess.run((self.cost, self.optimizer),
feed_dict={self.x: X, self.scale: self.training_scale})
return cost
# 讓session執行一個計算圖節點self.cost，在測試會用到
def calc_total_cost(self, X):
return self.sess.run(self.cost,
feed_dict={self.x: X, self.scale: self.training_scale})
# 返回自編碼器隱含層的輸出結果，目的是提供一個介面來獲取抽象後的特徵
def transform(self, X):
return self.sess.run(self.hidden, feed_dict={self.x: X,
self.scale: self.training_scale})
# generate函式，將隱含層的輸出結果作為輸入
# 通過之後的重建層將提取到的高階特徵復原為原始資料
def generate(self, hidden = None):
if hidden is None:
hidden = np.random.normal(size=self.weights['b1'])
return self.sess.run(self.reconstruction, feed_dict={self.hidden:hidden})
# 整體執行一遍復原過程，包括提取高階特徵和通過高階特徵復原資料
def reconstruct(self, X):
return self.sess.run(self.reconstruction, feed_dict={self.x: X,
self.scale: self.training_scale})
# 獲取隱含層的權重 W1
def getWeights(self):
return self.sess.run(self.weights['w1'])
# 獲取隱含層的偏置係數 b1
def getBiases(self):
return self.sess.run(self.weights['b1'])
# read data to load mnist dataset
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
def standard_scale(X_train, X_test):
# 標準化即讓資料變成0均值，且標準差為1的分佈
preprocessor = prep.StandardScaler().fit(X_train)
X_train = preprocessor.transform(X_train)
X_test = preprocessor.transform(X_test)
return X_train, X_test
# 定義一個獲取隨機block資料的函式，取一個從0到len(data)-batch_size之間的隨機整數
# 這裡是不放回抽樣，可以提高資料的利益效率
def get_random_block_from_data(data, batch_size):
start_index = np.random.randint(0, len(data) - batch_size)
return data[start_index: (start_index + batch_size)]
# 使用之前定義的standard_scale 函式對訓練集，測試集進行標準化變換
X_train, X_test = standard_scale(mnist.train.images, mnist.test.images)
n_samples = int(mnist.train.num_examples) # 總訓練樣本資料
training_epochs = 20 # 最大訓練的輪數
batch_size = 128 # 批次尺寸
display_step = 1
autoencoder = AdditiveGaussianNoiseAutoencoder(n_input=784,
n_hidden=200,
transfer_function=tf.nn.softplus,
optimizer=tf.train.AdamOptimizer(learning_rate=0.001),
scale=0.01)
for epoch in range(training_epochs):
avg_cost = 0
total_batch = int(n_samples / batch_size)
for i in range(total_batch):
batch_xs = get_random_block_from_data(X_train, batch_size)
cost = autoencoder.partial_fit(batch_xs)
avg_cost += cost / n_samples * batch_size
if epoch % display_step == 0:
print("Epoch:", '%04d' %(epoch + 1), 'cost=', "{:.9f}".format(avg_cost))
print("Total cost: " + str(autoencoder.calc_total_cost(X_test)))
結果如下：
Epoch: 0001 cost= 19994.269430682 Epoch: 0002 cost= 12152.192460227 Epoch: 0003 cost= 10875.503042045 Epoch: 0004 cost= 10308.418541477 Epoch: 0005 cost= 9187.305378977 Epoch: 0006 cost= 9217.541369886 Epoch: 0007 cost= 9685.120126136 Epoch: 0008 cost= 9682.280556250 Epoch: 0009 cost= 8886.662347727 Epoch: 0010 cost= 8706.033726705 Epoch: 0011 cost= 7810.424784091 Epoch: 0012 cost= 8669.721145455 Epoch: 0013 cost= 8534.551150568 Epoch: 0014 cost= 7741.216421591 Epoch: 0015 cost= 7924.397942045 Epoch: 0016 cost= 7475.140959091 Epoch: 0017 cost= 8064.848693750 Epoch: 0018 cost= 8351.518777273 Epoch: 0019 cost= 7844.633439773 Epoch: 0020 cost= 8505.549214773 Total cost: 634369.4
上面為訓練結果，我們將平均損失 avg_cost 設為0，並計算總共需要的 batch 數（通常樣本總數除以batch大小），注意這裡使用的時不放回抽樣，所以並不能保證每個樣本都被抽樣並參與訓練。然後在每一個 batch 的迴圈中，先使用 get_random_block_from_data 函式隨機抽取一個 block 的資料，然後使用成員函式 partial_fit 訓練這個 batch 的資料並計算當前的 cost，最後將當前的 cost 整合到 avg_cost 中，在每一輪迭代後，顯示當前的迭代數和這一輪迭代的平均 cost。我們在第一輪迭代時，cost 大約為19999，在最後一輪迭代時， cost大約為7000，再接著訓練 cost 也很難繼續降低了。當然可以繼續調整 batch_size，epoch數，優化器，自編碼器的隱含層數，隱含節點數等，來嘗試獲取更低的 cost 。
最後對訓練完的模型進行效能測試，這裡使用之前定義的成員函式 cal_total_cost 對測試集 X_test 進行測試，評價指標依然是平方誤差，如果使用示例中的引數，我們可以看到損失值為 60萬。
至此，去噪自編碼器的 TensorFlow完全實現。我們可以發現實現自編碼器和實現一個單隱含層的神經網路差不多，只不過是在資料輸入時做了標準化，並加上了一個高斯噪聲，同時我們在輸出結果不是數字分類結果，而是復原的資料，因此不需要用標註過的資料進行監督訓練。自編碼器作為一種無監督學習的方法，它與其他無監督學習的主要不同在於，它不是對資料進行聚類，而是提取其中最有用，最頻繁出現的高階特徵，根據這些高階特徵重構資料。在深度學習發展早期非常流行的 DBN，也是依靠這種思想，先對資料進行無監督的學習，提取到一些有用的特徵，將神經網路權重初始化到一個較好的分佈，然後再使用有標註的資料進行監督訓練，即對權重進行 fine-tune。
現在，無監督式預訓練的使用場景比以前少了許多，訓練全連線的 MLP 或者 CNN，RNN 時，我們都不需要先使用無監督訓練提取特徵。但是無監督學習乃至 AutoEncoder 依然是非常有用的。現實生活中，大部分的資料都是沒有標註資訊的，但人腦就很擅長處理這些資料，我們會提取其中的高階抽象特徵，並使用在其他地方。自編碼器作為深度學習在無監督領域的嘗試是非常成功的，同時無監督學習也將是深度學習接下來的一個重要發展方向。
3，pytorch實現自動編碼器
3.1 什麼是自動編碼器
自動編碼器（AutoEncoder）最開始作為一種資料的壓縮方法，其特點有：
（1） 跟資料相關程式很高，這意味著自動編碼器只能壓縮與訓練資料相似的資料，這個其實比較顯然，因為使用神經網路提取的特徵一般是高度相關於原始的訓練集，使用人臉訓練出來的自動編碼器在壓縮自然界動物的圖片是表現就會比較差，因為它只學習到了人臉的特徵，而沒有能夠學習到自然界圖片的特徵；
（2）壓縮後的資料是有損的，這是因為在降維過程中不可避免的要丟掉資訊
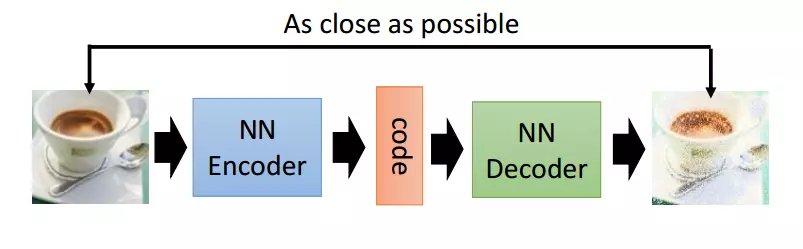
Autoencoder 簡單來說就是將有很多Feature的資料進行壓縮，之後再進行解壓的過程。比如有一個神經網路，它在做的事情是接收一張圖片，然後給他打碼，最後，再從打碼後的圖片中還原，如下圖：
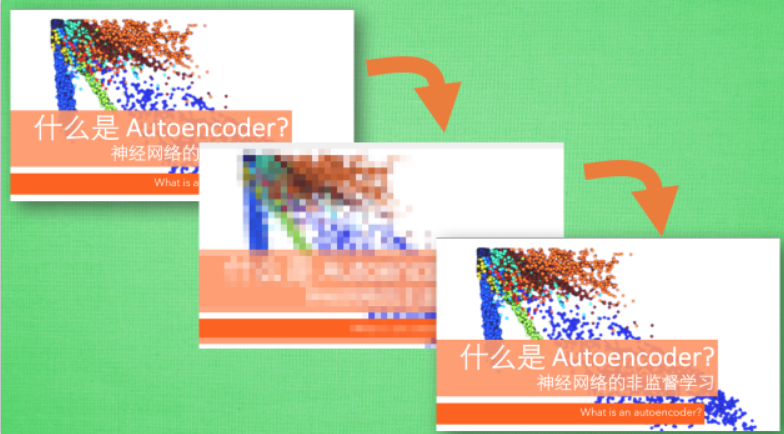
因為有時候神經網路要接受大量的輸入資訊，比如輸入資訊是高清圖片時，輸入資訊量可能達到上千萬，讓神經網路直接從上千萬個資訊源中學習是一件很吃力的工作。所以，壓縮一下，提取出原圖片中的最具有代表性的資訊，縮減輸入資訊量，再將縮減過後的資訊放入神經網路學習，這樣學習就簡單輕鬆了。
對於此問題來說，自編碼在這時候就能發揮作用，通過將原資料白色的X壓縮，解壓成黑色的X，然後通過對比黑白X，求出預測誤差，進行反向傳遞，逐步提升自編碼的準確性。訓練好的自編碼中間這一部分就是能總結元資料的精髓。
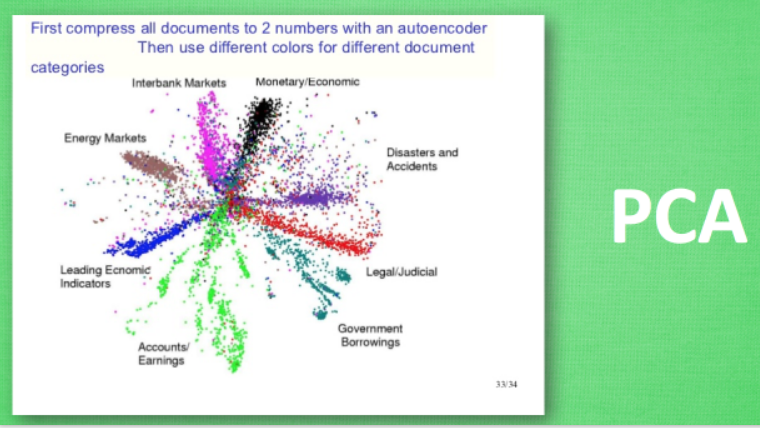
對於自編碼，我們只用了輸入資料X，並沒用到X對應的資料標籤，所以也可以說自編碼是一種非監督學習。如果大家知道PCA（Principal component analysis），與Autoencoder相類似，它的主要功能即使對資料進行非監督學習，並將壓縮站會後得到的“特徵值”，這一中間結果正類似於PCA的結果。之後再將壓縮過的“特徵值”進行解壓，得到的最終結果與原始資料進行比較，對此進行非監督學習。其大概過程如下：
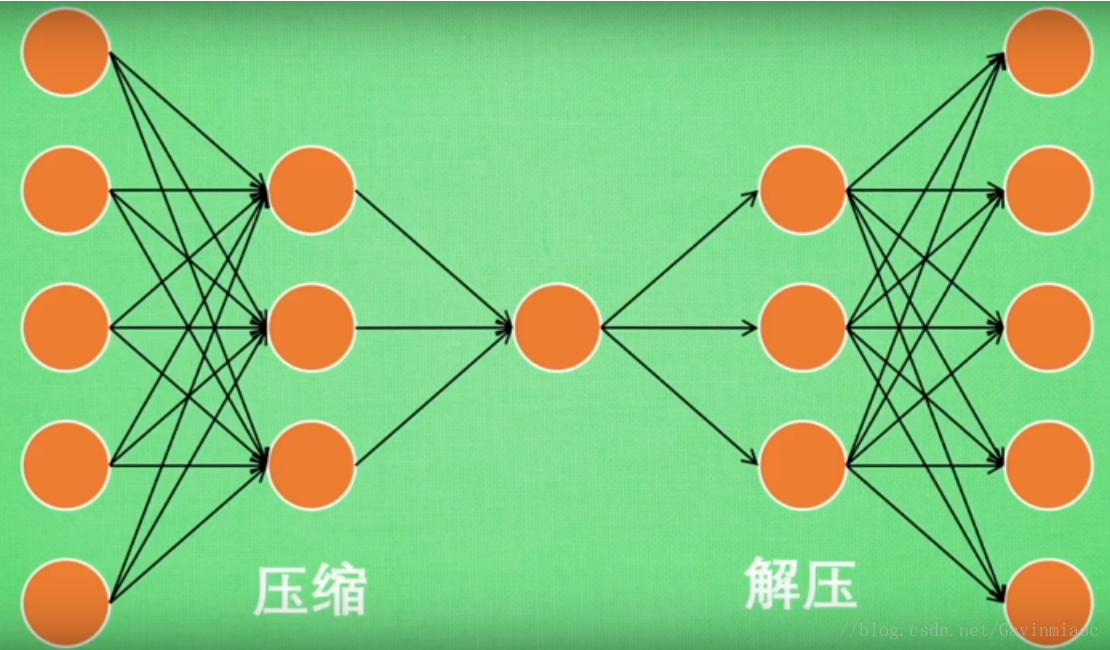
這是一個通過自編碼整理出來的資料，它能從元資料中總結出每種型別資料的特徵，如果把這些特徵型別都放在一張二維的圖片上 ，每種型別都已經很好地用原資料的精髓區分來。如果你瞭解PCA主成分，再提取主要特徵時，自編碼和他一樣，甚至超越了PCA，換句話說，自編碼可以像PCA一樣給特徵屬性降維。
3.2 編碼器的學習
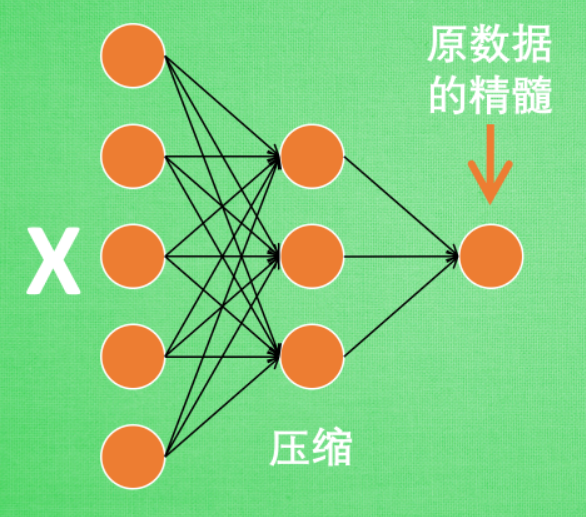
這部分叫做encoder編碼器，編碼器能得到元資料的精髓，然後我們只需要再建立一個小的神經網路學習這個精髓的資料，不僅減少了神經網路的負擔，同樣也能達到很好的效果。
3.3 解碼器的學習
至於解碼器Decoder，我們知道，它在訓練的時候是要將精髓資訊解壓成原始資訊，那麼這就提供了一個解壓器的作用，甚至我們可以認為是一個生成器（類似於GAN），那做這件事的一種特殊自編碼叫做variational autoencoders。
有一個例子就是讓它能模仿並生成手寫數字：
3.4 程式碼解析
今天的程式碼，我們會運用兩個型別：
- 1，是通過Feature的壓縮並解壓，並將結果與原始資料進行對比，觀察處理過後的資料是不是如預期跟原始資料很相似（這裡會用到MNIST資料）
- 2，我們只看encoder壓縮的過程，使用它將一個數據集壓縮到只有兩個Feature時，將資料放入一個二維座標系內。
神經網路也能進行非監督學習，只需要訓練資料，不需要標籤資料。自編碼就是這樣一種形式。自編碼能自動分類資料，而且也能巢狀在半監督學習的上面，用少量的有標籤樣本和大量的無標籤樣本學習。
這次學習用MNIST手寫資料來壓縮再解壓圖片。
然後用壓縮的特徵進行非（無）監督分類。
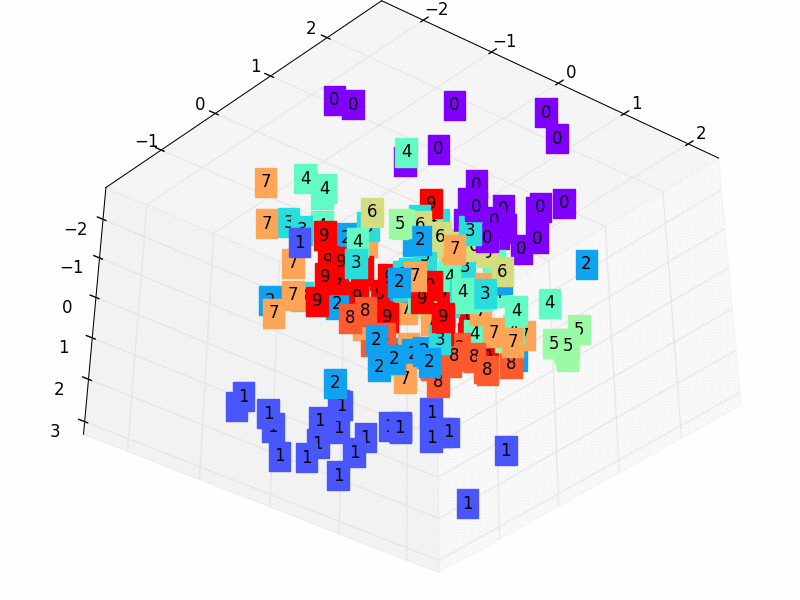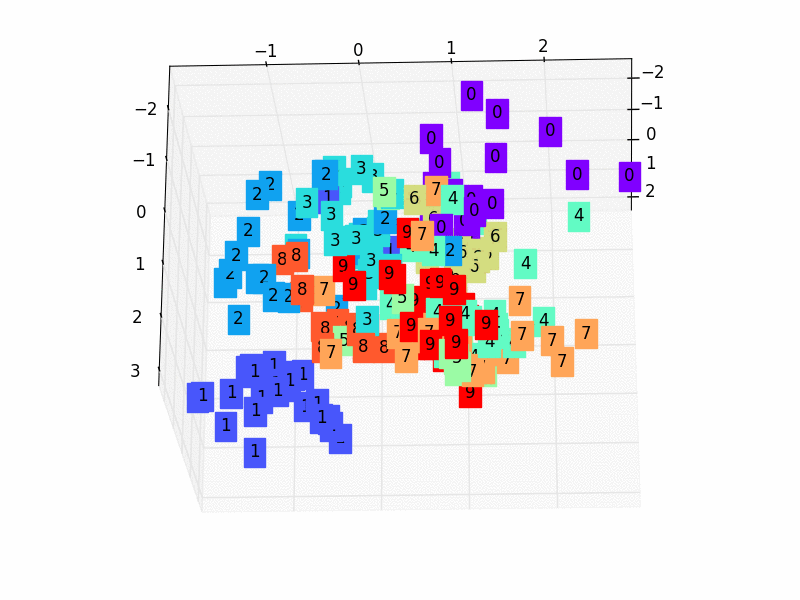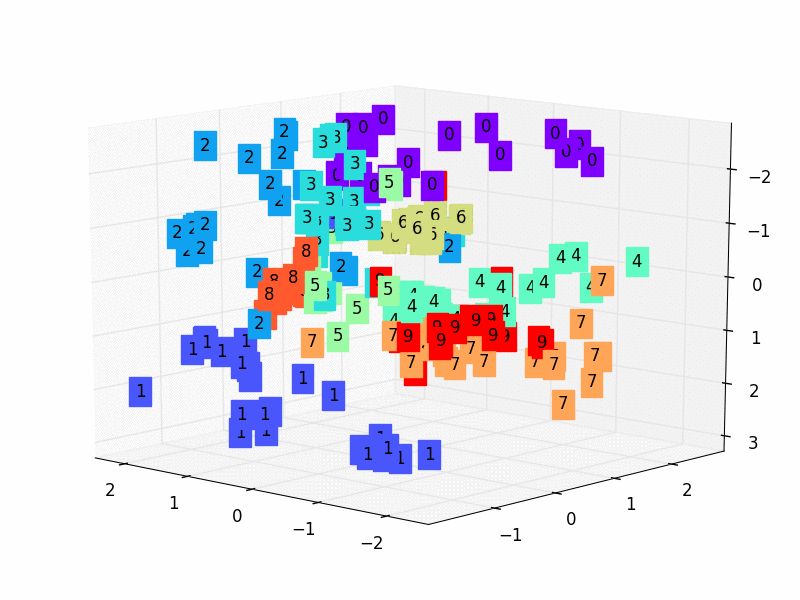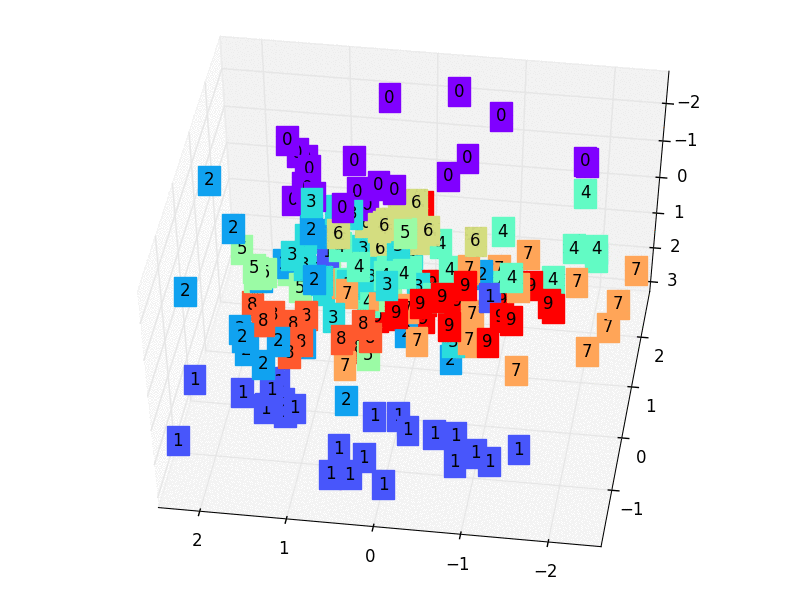
3.5 訓練資料
自編碼只能用訓練集就好了，而且只需要訓練training data 的 image， 不用訓練labels。
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
# 超引數
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005
# 下過資料的話, 就可以設定成 False
DOWNLOAD_MNIST = True
# 到時候顯示 5張圖片看效果, 如上圖一
N_TEST_IMG = 5
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./mnist/',
# this is training data
train=True,
# Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
transform=torchvision.transforms.ToTensor(),
# download it if you don't have it
download=DOWNLOAD_MNIST,
)
3.6 AutoEncoder
AutoEncoder 的形式很監督，分別是encoder 和 decoder，壓縮和解壓，壓縮後得到壓縮的特徵值，再從壓縮的特徵值解壓成原圖片。
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
# 壓縮
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.Tanh(),
nn.Linear(128, 64),
nn.Tanh(),
nn.Linear(64, 12),
nn.Tanh(),
nn.Linear(12, 3), # 壓縮成3個特徵, 進行 3D 影象視覺化
)
# 解壓
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.Tanh(),
nn.Linear(12, 64),
nn.Tanh(),
nn.Linear(64, 128),
nn.Tanh(),
nn.Linear(128, 28*28),
nn.Sigmoid(), # 激勵函式讓輸出值在 (0, 1)
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return encoded, decoded
autoencoder = AutoEncoder()
這裡我們定義了一個簡單的四層網路作為編碼器，中間使用ReLU啟用函式，最後輸出的是三維的。輸出一個28 * 28 的影象資料，特別要注意的是最後使用的啟用函式是Tanh，這個啟用函式能夠將最後的輸出轉換到 -1 和 1 之間，這是因為我們輸入的圖片已經變換到 -1 和 1 之間了，這是的輸出必須和其對應。
我們也可以將多層感知器換成卷積神經網路，這樣對圖片的特徵提取有著更好的效果。
class autoencoder(nn.Module):
def __init__(self):
super(autoencoder, self).__init__()
self.encoder = nn.Sequential(
nn.Conv2d(1, 16, 3, stride=3, padding=1), # b, 16, 10, 10
nn.ReLU(True),
nn.MaxPool2d(2, stride=2), # b, 16, 5, 5
nn.Conv2d(16, 8, 3, stride=2, padding=1), # b, 8, 3, 3
nn.ReLU(True),
nn.MaxPool2d(2, stride=1) # b, 8, 2, 2
)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(8, 16, 3, stride=2), # b, 16, 5, 5
nn.ReLU(True),
nn.ConvTranspose2d(16, 8, 5, stride=3, padding=1), # b, 8, 15, 15
nn.ReLU(True),
nn.ConvTranspose2d(8, 1, 2, stride=2, padding=1), # b, 1, 28, 28
nn.Tanh()
)
def forward(self, x):
x = self.encoder(x)
x = self.decoder(x)
return x
這裡使用了 nn.ConvTranspose2d()，這可以看做是卷積的反操作，可以在某種意義上看做是反捲積。
3.7 訓練並可視化
訓練，並可視化訓練的過程，我們可以有效的利用encoder 和decoder來做很多事情，比如這裡我們用decoder的資訊輸出看和原圖片的對比，還能用encoder來看經過壓縮後，神經網路對原圖片的理解。encoder能將不同圖片資料大概的分離開來，這樣就是一個無監督學習的過程。
而訓練過程也比較簡單，我們使用最小均方誤差來作為損失函式，比較生成的圖片與原始圖片的每個畫素點的差異。
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()
for epoch in range(EPOCH):
for step, (x, b_label) in enumerate(train_loader):
b_x = x.view(-1, 28*28) # batch x, shape (batch, 28*28)
b_y = x.view(-1, 28*28) # batch y, shape (batch, 28*28)
encoded, decoded = autoencoder(b_x)
loss = loss_func(decoded, b_y) # mean square error
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
所有程式碼如下：
import torch
import torch.nn as nn
import torch.utils.data as Data
import torchvision
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
import numpy as np
# torch.manual_seed(1) # reproducible
# Hyper Parameters
EPOCH = 10
BATCH_SIZE = 64
LR = 0.005 # learning rate
DOWNLOAD_MNIST = False
N_TEST_IMG = 5
# Mnist digits dataset
train_data = torchvision.datasets.MNIST(
root='./mnist/',
train=True, # this is training data
transform=torchvision.transforms.ToTensor(), # Converts a PIL.Image or numpy.ndarray to
# torch.FloatTensor of shape (C x H x W) and normalize in the range [0.0, 1.0]
download=DOWNLOAD_MNIST, # download it if you don't have it
)
# plot one example
print(train_data.train_data.size()) # (60000, 28, 28)
print(train_data.train_labels.size()) # (60000)
plt.imshow(train_data.train_data[2].numpy(), cmap='gray')
plt.title('%i' % train_data.train_labels[2])
plt.show()
# Data Loader for easy mini-batch return in training, the image batch shape will be (50, 1, 28, 28)
train_loader = Data.DataLoader(dataset=train_data, batch_size=BATCH_SIZE, shuffle=True)
class AutoEncoder(nn.Module):
def __init__(self):
super(AutoEncoder, self).__init__()
self.encoder = nn.Sequential(
nn.Linear(28*28, 128),
nn.Tanh(),
nn.Linear(128, 64),
nn.Tanh(),
nn.Linear(64, 12),
nn.Tanh(),
nn.Linear(12, 3), # compress to 3 features which can be visualized in plt
)
self.decoder = nn.Sequential(
nn.Linear(3, 12),
nn.Tanh(),
nn.Linear(12, 64),
nn.Tanh(),
nn.Linear(64, 128),
nn.Tanh(),
nn.Linear(128, 28*28),
nn.Sigmoid(), # compress to a range (0, 1)
)
def forward(self, x):
encoded = self.encoder(x)
decoded = self.decoder(encoded)
return encoded, decoded
autoencoder = AutoEncoder()
optimizer = torch.optim.Adam(autoencoder.parameters(), lr=LR)
loss_func = nn.MSELoss()
# initialize figure
f, a = plt.subplots(2, N_TEST_IMG, figsize=(5, 2))
plt.ion() # continuously plot
# original data (first row) for viewing
view_data = train_data.train_data[:N_TEST_IMG].view(-1, 28*28).type(torch.FloatTensor)/255.
for i in range(N_TEST_IMG):
a[0][i].imshow(np.reshape(view_data.data.numpy()[i], (28, 28)), cmap='gray'); a[0][i].set_xticks(()); a[0][i].set_yticks(())
for epoch in range(EPOCH):
for step, (x, b_label) in enumerate(train_loader):
b_x = x.view(-1, 28*28) # batch x, shape (batch, 28*28)
b_y = x.view(-1, 28*28) # batch y, shape (batch, 28*28)
encoded, decoded = autoencoder(b_x)
loss = loss_func(decoded, b_y) # mean square error
optimizer.zero_grad() # clear gradients for this training step
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if step % 100 == 0:
print('Epoch: ', epoch, '| train loss: %.4f' % loss.data.numpy())
# plotting decoded image (second row)
_, decoded_data = autoencoder(view_data)
for i in range(N_TEST_IMG):
a[1][i].clear()
a[1][i].imshow(np.reshape(decoded_data.data.numpy()[i], (28, 28)), cmap='gray')
a[1][i].set_xticks(()); a[1][i].set_yticks(())
plt.draw(); plt.pause(0.05)
plt.ioff()
plt.show()
# visualize in 3D plot
view_data = train_data.train_data[:200].view(-1, 28*28).type(torch.FloatTensor)/255.
encoded_data, _ = autoencoder(view_data)
fig = plt.figure(2); ax = Axes3D(fig)
X, Y, Z = encoded_data.data[:, 0].numpy(), encoded_data.data[:, 1].numpy(), encoded_data.data[:, 2].numpy()
values = train_data.train_labels[:200].numpy()
for x, y, z, s in zip(X, Y, Z, values):
c = cm.rainbow(int(255*s/9)); ax.text(x, y, z, s, backgroundcolor=c)
ax.set_xlim(X.min(), X.max()); ax.set_ylim(Y.min(), Y.max()); ax.set_zlim(Z.min(), Z.max())
plt.show()
4，變分自動編碼器（Variational Auoencoder）
變分編碼器是自動編碼器的升級版本，其結構根自動編碼器是類似的，也由編碼器和解碼器構成。
自動編碼器就是需要輸入一張圖片，然後將一張圖片編碼之後得到一個隱含向量，這比我們隨機取一個隨機噪聲更好，因為這包含著原圖片的資訊，然後我們隱含向量解碼得到與原圖片對應的照片。
但是這樣我們其實並不能任意生成圖片，因為我們沒有辦法自己去構造隱藏向量，我們需要通過一張圖片輸入編碼我們才知道得到的隱含向量是什麼，這時我們就可以通過變分自動編碼器來解決這個問題。
其實原理特別簡單，只需要在編碼過程中給它增加一些限制，迫使其生產的隱含向量能夠粗略的遵循一個標準正態分佈，這就是與一般的自動編碼器最大的不同。
這樣我們生產一張新的圖片就很簡單了，我們只需要給它一個標準正態分佈的隨機隱含向量，這樣通過解碼器就能生成我們想要的圖片，而不需要給他一張原始圖片先編碼。
在實際情況中，我們需要在模型的準確率上與隱含向量服從標準正態分佈之間做一個權衡，所謂模型的準確率就是指解碼器生成的圖片與原圖片的相似程度。我們可以讓網路自己來做這個決定，非常簡單，我們只需要將這兩者都做一個loss，然後在將他們求和作為總的loss，這樣網路就能夠自己選擇如何才能夠使得這個總的loss下降。另外我們要衡量兩種分佈的相似程度，如何看過之前一片GAN的數學推導，你就知道會有一個東西叫KL divergence來衡量兩種分佈的相似程度，這裡我們就是用KL divergence來表示隱含向量與標準正態分佈之間差異的loss，另外一個loss仍然使用生成圖片與原圖片的均方誤差來表示。
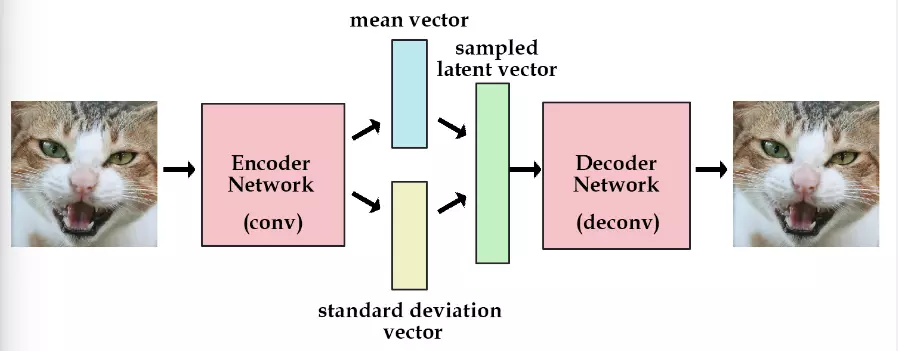這時不再是每次產生一個隱含向量，而是生成兩個向量，一個表示均值，一個表示標準差，然後通過這兩個統計量來合成隱含向量，這也非常簡單，用一個標準正態分佈先乘上標準差再加上均值就行了，這裡我們預設編碼之後的隱含向量是服從一個正態分佈的。這個時候我們是想讓均值儘可能接近0，標準差儘可能接近1。而論文裡面有詳細的推導如何得到這個loss的計算公式，有興趣的同學可以去看看推導
下面是PyTorch的實現：
reconstruction_function = nn.BCELoss(size_average=False) # mse loss
def loss_function(recon_x, x, mu, logvar):
"""
recon_x: generating images
x: origin images
mu: latent mean
logvar: latent log variance
"""
BCE = reconstruction_function(recon_x, x)
# loss = 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
KLD_element = mu.pow(2).add_(logvar.exp()).mul_(-1).add_(1).add_(logvar)
KLD = torch.sum(KLD_element).mul_(-0.5)
# KL divergence
return BCE + KLD
另外變分編碼器除了可以讓我們隨機生成隱含變數，還能夠提高網路的泛化能力、
最後是VAE的程式碼實現：
class VAE(nn.Module):
def __init__(self):
super(VAE, self).__init__()
self.fc1 = nn.Linear(784, 400)
self.fc21 = nn.Linear(400, 20)
self.fc22 = nn.Linear(400, 20)
self.fc3 = nn.Linear(20, 400)
self.fc4 = nn.Linear(400, 784)
def encode(self, x):
h1 = F.relu(self.fc1(x))
return self.fc21(h1), self.fc22(h1)
def reparametrize(self, mu, logvar):
std = logvar.mul(0.5).exp_()
if torch.cuda.is_available():
eps = torch.cuda.FloatTensor(std.size()).normal_()
else:
eps = torch.FloatTensor(std.size()).normal_()
eps = Variable(eps)
return eps.mul(std).add_(mu)
def decode(self, z):
h3 = F.relu(self.fc3(z))
return F.sigmoid(self.fc4(h3))
def forward(self, x):
mu, logvar = self.encode(x)
z = self.reparametrize(mu, logvar)
return self.decode(z), mu, logvar
VAE 的結果比普通的自動編碼器要好很多，下面是結果（左邊是原圖 ，右邊是自動編碼）：
VAE的缺點也很明顯，他是直接計算生成圖片和原始圖片的均方誤差而不是像GAN那樣去對抗來學習，這就使得生成的圖片會有點模糊。現在已經有一些工作是將VAE和GAN結合起來，使用VAE的結構，但是使用對抗網路來進行訓練，具體可以參考一下這篇論文。
5，多層感知機學習
在之前學習的 TensorFlow學習筆記——使用TensorFlow操作MNIST資料（1）。我們實現了一個簡單的 Softmax Regression 模型，這個線性模型最大的特點是簡單易用，但是擬合能力不強。Softmax Regression 可以算是多分類問題 logistic regression ，它進而傳統意義上的神經網路的最大區別是哪些沒有隱含層。隱含層是神經網路一個重要概念。它是指除輸出，輸出層外，中間的哪些層。輸入層和輸出層是對外可見的，因此也可以被稱作可視層，而中間層不直接暴露出來，是模型的黑箱部分，通常也比較難具有可解釋性，所以一般被稱作隱含層。有了隱含層，神經網路就具有了一些特殊的屬性，比如引入非線性的隱含層後，理論上只要隱含層節點足夠多，即使只有一個隱含層的神經網路也可以擬合任意函式。同時隱含層越多，越容易擬合複雜函式。有理論研究表明，為了擬合複雜函式需要的隱含節點的數目，基本上隨著隱含層的數量增多呈指數下降趨勢。也就是說層數越多，神經網路所需要的隱含節點可以越少。這也是深度學習的特點之一，層數越深，概念越抽象，需要背誦的知識點（神經網路隱含節點）就越少。不過實際使用中，使用層數較深的神經網路會遇到許多困難，比如容易過擬合，引數難以除錯，梯度彌散等等。對這些問題我們需要很多 Trick 來解決，在最近幾年的研究中心，越來越多的方法，比如Dropout，Adagrad，ReLUdeng ，逐漸幫助我們解決了一部分問題。
過擬合是機器學習中一個常見的問題，它是指模型預測準確率在訓練集上升高，但是在測試集上反而下降了，這通常意味著泛化性不好，模型只是記憶了當前資料的特徵，不具備推廣能力，尤其是在神經網路中，因為引數眾多，經常出現引數比資料還要多的情況，這就非常容易出現只是記憶了訓練集特徵的情況。為了解決這個問題，Hinton教授團隊提出了一個思路簡單但是非常有效的方法，Dropout。在使用複雜的卷積神經網路訓練影象資料時尤其有效，它的大致思路是在訓練時，將神經網路某一層的輸出節點資料隨機丟棄一部分。我們可以理解為隨機把一張圖片50%的點刪除掉（即隨機將50%的點變成黑點），此時人還是很可能識別出這種圖片的型別，當時機器也是可以的。這種做法實質上等於創造出了許多新的隨機樣本，通過增大樣本量，減少特徵數量來防止過擬合。Dropout 其實也算一種 bagging 方法，我們可以理解成每次丟棄節點資料是對特徵的一種取樣。相當於我們訓練一個 ensemble 的神經網路模型，對每個樣本都做特徵取樣，只不過沒有訓練多個神經網路模型，只要一個融合的神經網路。
引數難以除錯時神經網路的另一大痛點，尤其是SGD的引數，對SGD設定不同的學習速率，最後得到的結果可能差距巨大。神經網路通常不是一個凸優化的問題，它處處充滿了區域性最優。SGD本身也不是一個比較穩定的演算法，結果可能會在最優解附近波動，而不同的學習速率可能導致神經網路落入截然不同的區域性最優之中。不過，通常我們也並不指望能達到全域性最優，有理論表示，神經網路可能有很多個區域性最優解都可以達到比較好的分類效果，而全域性最優反而是比較容易過擬合的解。我們也可以從人來類推，不同的人有各自迥異的腦神經連線，沒有兩個人的神經連線方式能完全一致，就像沒有兩個人的見解能完全相同，但是每個人的腦神經網路（區域性最優解）對識別圖片中物體類別都有很不錯的效果。對SGD，一開始我們可能希望學習速率大一些，可以加速收斂，但是訓練的後期又希望學習速率可以小一些，這樣可以比較穩定的落入一個區域性最優解。不同的機器學習問題所需要的學習速率也不太好設定，需要反覆除錯，因此就像有 Adagrad, Adam, Adadelta 等自適應的方法可以減輕除錯引數的負擔。對於這些優化演算法，通常我們使用它預設的引數設定就可以取得一個比較好的效果。而SGD則需要對學習速率，Momentum, Nesterov 等引數進行比較複雜的除錯，當除錯的引數較為適合問題時，才能達到比較好的效果。
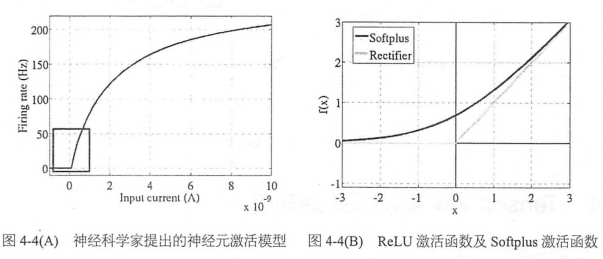
梯度彌散（Gradient Vanishment）是另一個影響深層神經網路訓練的問題，在ReLU啟用函數出現之前，神經網路訓練全部都是用 Sigmoid 作為啟用函式。這可能是因為 Sigmoid 函式具有侷限性，輸出數值在0~1 ，最符合概率輸出的定義。非線性的Sigmoid 函式在訊號的特徵空間對映上，對中央區的資訊增益較大，對兩側區的訊號增益小。從生物神經科學的角度來看，中央區酷似神經元的興奮態，兩側區酷似神經元的抑制態。因而在神經網路訓練時，可以將重要特徵置於中央區，將非中央特徵置於兩側區。可以說，Sigmoid比最初期的線性啟用函式 y=x ，階梯啟用函式 y=x ，階梯啟用函式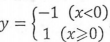 
和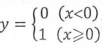
好了不少。但是當神經網路層數較多時，Sigmoid函式在反向傳播中梯度值會逐漸減少，經過多層的傳遞後會呈現指數級急劇下降，因此梯度值在傳遞到前面幾層時就變得非常小了。這種情況下，根據訓練資料的反饋來更新神經網路的引數將會非常緩慢，基本起不到訓練的作用。直到ReLU 的出現，才比較完美的解決了梯度彌散的問題。ReLU是非常簡單的非線性函式 Y=max(0, x)，它在座標軸上式一條折線，當x<=0時，y=0；當x>0時， y=x，非常類似於人腦閾值響應機制。訊號在超過某個閾值時，神經元才會進入興奮和啟用的狀態，平時則處於抑制狀態。ReLU可以很好地傳遞梯度，經過多層的反向傳播，梯度依舊不會大幅縮小，因此非常適合訓練很深的神經網路。ReLU從正面解決了梯度彌散的問題，而不需要通過無監督的逐層訓練初始化權重來繞行。
ReLU對比 Sigmoid 的主要變化有如下三點：
- 1，單側抑制
- 2，相對寬闊的興奮邊界
- 3，稀疏啟用性
神經科學家在進行大腦能量消耗的研究中發現，神經元編碼的工作方式具有稀疏性，推測大腦同時被啟用的神經元只有1%~4%。神經元只會對輸入訊號有少部分的選擇性響應，大量不相關的訊號被遮蔽，這樣可以更高效的提取重要特徵。傳統的Sigmoid函式則有接近一半的神經元被啟用，不符合神經科學的研究。Softplus雖然有單側抑制，卻沒有稀疏啟用性，因而ReLU函式 max(0, x) 成了最符合實際神經元的模型。目前，ReLU及其變種（EIU34，PReLU35,RReLU36）已經成為了最主流的啟用函式。實踐中大部分情況下（包含MLP和CNN，RNN內部主要還是使用 Sigmoid，Tanh，Hard Sigmoid）將隱含層的啟用函式從 Sigmoid 替換為ReLU都可以帶來訓練速度及模型準確率的提升。當然神經網路的輸出層一般都還是Sigmoid函式，因為他最接近概率輸出分佈。
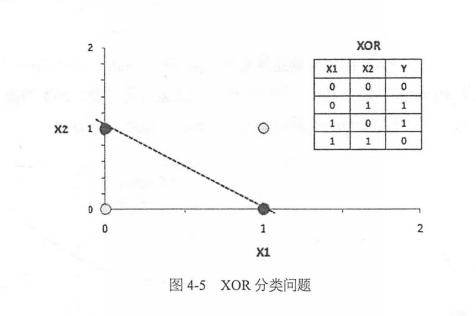
上面三段分別提到了可以解決多層神經網路問題的Dropout，Adagrad，ReLU等，那麼多層神經網路到底有什麼顯著的能力值得大家探索呢？或者說神經網路的隱含層到底有什麼用呢？隱含層的一個代表性的功能是可以解決XOR問題。在早期神經網路的研究中，有學者提出一個尖銳的問題，當時（沒有隱含層）的神經網路無法解決XOR的問題。如下圖所示，假設我們有兩個維度的特徵，並且有兩類樣本，（0， 0），（1， 1）是灰色，（0, 1）， （1， 0）是黑色，在這個特徵空間中這兩類樣本時線性不可分的，也就是說，我們無法用一條直線把灰，黑兩類分卡。沒有隱含層的神經網路時線性的，所以不可能對著兩類樣本進行正確的區分。這是早期神經網路的致命弱點，也直接導致了當時神經網路研究的低谷。當引入了隱含層並使用非線性的啟用函式（如Sigmoid，ReLU）後，我們可以使用曲線劃分兩類樣本，可以輕鬆的解決XOR異或函式的分類問題。這就是多層神經網路（或多層感知器，Multi-Layer Perceptron，MLP）的功能所在。
接下來，我們通常例子展示在僅加入一個隱含層的情況下，神經網路對MNIST資料集的分類項能就有顯著的提升，可以達到98%的準確率。當然這裡使用了Dropout，Adagrad，ReLU等輔助性元件。
6，TensorFlow實現多層感知機
在之前使用TensorFlow實現一個完整的Softmax Regression（無隱含層）並在MNIST資料集上取得了大約92%的正確率。下面實現多層感知機依然使用 MNIST資料集，現在要給審計網路加上隱含層，並使用減輕過擬合的Dropout，自適應學習速率的Adagrad，以及可以解決梯度彌散的啟用函式ReLU。
程式碼：
#_*_coding:utf-8_*_
from tensorflow.examples.tutorials.mnist import input_data
import tensorflow as tf
mnist = input_data.read_data_sets('MNITS_data/', one_hot=True)
# 建立一個預設的InteractiveSession，這樣後面執行各項操作就無須指定Session
sess = tf.InteractiveSession()
in_uints = 784 # 輸入節點數
# 在此模型中隱含層的節點數設定在200~1000範圍內結果區別都不大
h1_uints = 300 # 隱含層的輸出節點數設為300
# W1 b1是隱含層的權重和偏置,將偏置全部賦值為0
# 並將權重初始化為截斷的正態分佈，其標註差為0.1
W1 = tf.Variable(tf.truncated_normal([in_uints, h1_uints], stddev=0.1))
b1 = tf.Variable(tf.zeros([h1_uints]))
W2 = tf.Variable(tf.zeros([h1_uints, 10]))
b2 = tf.Variable(tf.zeros([10]))
# 由於在訓練和預測時，Dropout的比率keep_prob（即保留節點的概率）是不一樣的
x = tf.placeholder(tf.float32, [None, in_uints])
keep_prob = tf.placeholder(tf.float32)
# 定義模型結構,神經網路forward時的計算
hidden1 = tf.nn.relu(tf.matmul(x, W1) + b1)
hidden1_drop = tf.nn.dropout(hidden1, keep_prob)
y = tf.nn.softmax(tf.matmul(hidden1_drop, W2) + b2)
y_ = tf.placeholder(tf.float32, [None, 10])
cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y),
reduction_indices=[1]))
train_step = tf.train.AdagradOptimizer(0.3).minimize(cross_entropy)
# 訓練模型
tf.global_variables_initializer().run()
for i in range(3000):
batch_xs, batch_ys = mnist.train.next_batch(100)
# 我們加入了keep_prob作為計算圖的輸入，並在訓練時候設為0.75，其餘的0.25置為0
train_step.run({x: batch_xs, y_: batch_ys, keep_prob: 0.75})
# 對模型進行準確率評測, 加入一個keep_prob作為輸入
# 因為預測部分，所以我們直接令keep_prob=1即可，這樣可以達到模型最好的預測效果
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(accuracy.eval({x: mnist.test.images, y_: mnist.test.labels,
keep_prob: 1.0}))
訓練的時候，這裡加入了keep_prob作為計算圖的輸入，並且在訓練時設為0.75，即保留75%的節點，其餘的25%置為0。一般來說，對越複雜越大規模的神經網路，Dropout的效果越顯著。另外，因為加入了隱含層，我們需要更多的訓練迭代來優化模型引數以達到一個比較好的效果。所以一共採用了3000個 batch，每個 batch包含100個樣本，一共30萬的樣本，相當於對全資料集進行了5輪（epoch）迭代。如果增加迴圈次數，準確率也會略有提高。
結果如下：
0.9778
最終，我們在測試集上可以達到97.78%的準確率。相比之前的Softmax，我們的誤差率由8%下降到2%，對識別銀行賬單這種精確度要求很高的場景，可以說是飛躍性的提高。而這個提升僅增加一個隱含層就實現了，可見多層神經網路的效果有多顯著。當然，其實我們也使用了一些Trick 進行輔助，比如 Dropout，Adagrad，ReLU等，但是起決定性作用的還是隱含層本身，它能對特徵進行抽象和轉化。
沒有隱含層的Softmax Regression 只能直接從影象的畫素點推斷是哪個數字，而沒有特徵抽象的過程。多層神經網路依靠隱含層，則可以組合出高階特徵，比如橫線，豎線，圓圈等，之後可以將這些高階特徵或者說元件再組合成數字，就能實現精準的匹配和分類。隱含層輸出的高階特徵（元件）經常是可以複用的，所以每一類的判別，概率輸出都共享這些高階特徵，而不是各自連線獨立的高階特徵。
同時我們可以發現，新加一個隱含層，並使用了Dropout，Adagrad和ReLU，而程式碼沒有增加很多，這就是TensorFlow的優勢之一。它的程式碼非常簡潔，沒有太多的冗餘，可以方便地將有用的模組拼裝在一起。
參考文獻：
https://github.com/L1aoXingyu/pytorch-beginner/tree/master/08-AutoEncoder http://kvfrans.com/variational-autoencoders-explained/ 此文是自己的學習筆記總結，學習於《TensorFlow實戰》，俗話說，好記性不如爛筆頭，寫寫總是好的，所以若侵權，請聯絡我，謝謝