布隆過濾器及其數學推導
目錄
- 布隆過濾器
- 什麼是布隆過濾器
- 原理簡介
- 數學推導
布隆過濾器
昨天突然看到了一個布隆過濾器的介紹和一些用法,感覺很新奇,也很有意思,剛好趁著週末來寫一篇部落格。
什麼是布隆過濾器
布隆過濾器?難道是這個?E起來,然後阻擋地方的飛行道具並減少傷害?

NO!NO!NO!當然不是這個,一篇技術部落格怎麼會扯到遊戲呢?來來來,讓我們先看一下布隆的E技能。
| 堅不可摧 | E | 消耗法力:30/35/40/45/50冷卻時間:18/16/14/12/10 | 布隆朝一個方向舉起盾牌,持續3/3.25/3.5/3.75/4秒,並使來自目標方向的第一次攻擊變得無效。布隆還將攔截敵方的飛行道具,並將它們摧毀,減少30/32.5/35/37.5/40%的後續傷害。在舉盾期間,布隆獲得10%移動速度加成。 | |
|---|---|---|---|---|
 |
| |首先,我們設想一個場景,在某次開發中,你被要求你的網站的使用者名稱不能重複,你應該怎麼做?第一感覺當然就是將使用者名稱存到資料庫中間,然後當用戶註冊的時候,檢視資料庫是否存在這個使用者名稱即可。可是,當你的網站使用者量很大的時候比如說一億,查詢資料庫毋庸置疑是一個耗時的操作,這個時候,你突然想到了雜湊表,因為你知道雜湊表的查詢時間複雜度是O(1),可是我們可以算一,一個使用者名稱為四個漢字,一個漢字佔用兩個位元組(Unicode情況下),那麼一共有八億個位元組。一共佔用763M的記憶體(這個裡面不包括物件佔用的空間,也不包括雜湊表中浪費的空間),而實際情況佔用的空間會比這個多得多。
那麼有什麼好方法解決這個問題呢?這個就是我們要講的布隆過濾器。首先我們以布隆的技能來形象的解釋下布隆過濾器的優缺點:
- 並使來自目標方向的第一次攻擊變得無效:如果布隆過濾器判斷資料不存在則資料絕對不存在。
- 布隆還將攔截敵方的飛行道具:這個就是布隆過濾器的特點,資料先經過布隆過濾器,查詢資料是否已經存在。如果布隆過濾器判斷使用者名稱不存在/或者存在,資料才能夠繼續向下走。
- 減少30/32.5/35/37.5/40%的後續傷害:在前面的判斷中,可以判斷資料絕對不存在,但是如果判斷資料存在,則資料也可能不存在。
- 技能加點是不能取消的:布隆過濾器只能插入資料,而不能刪除資料。
原理簡介
布隆過濾器的原理和雜湊表的原理有點類似,同樣需要使用hash函式,但是在布隆過濾器中,需要使用多個hash函式。布隆過濾器的原理還是比較簡單的。
我們有一個位數組bitArray,對,就是一個位數組,長度位m。只存0和1那種。此時我們有一個key,和k個hash函式,因此我們可以得到k個key被hash過後的數。然後我們分別對hash過後的值取餘(對m取餘)得到x,然後將bitArray中x位置置為1。
原理圖片如下所示(圖片來源)
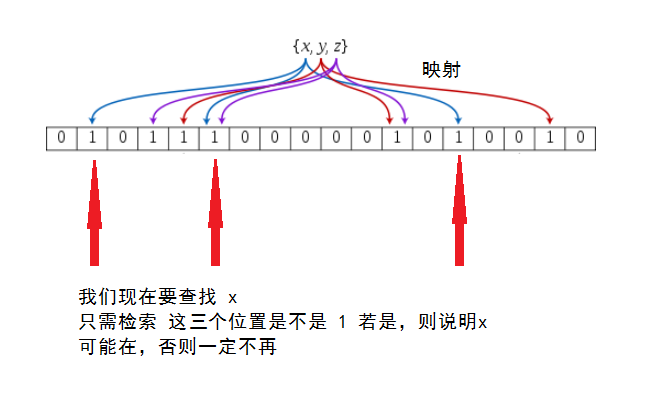
在前面我們介紹過布隆過濾器如果判斷資料存在,實際上資料也可能不存在。如果將布隆過濾器應用於垃圾郵件過濾系統,則就會出現“寧可錯殺一千,也決不放過一個”的這種情況。那麼為什麼會造成這種情況呢?實際上,這就和雜湊表中雜湊衝突的情況一樣,因為可能會出現兩個key值經過k個hash函式之後,取餘之後的結果是一樣的。所以,在布隆過濾器中可能會出現誤判,所以有一個概念叫做誤算率。
數學推導
上面我們知道布隆過濾器中,有一個誤算率,當然我們是想將誤判降低到最小(key的數量和陣列bitArray的長度都是確定的)。so,讓我們用數學公式來推導一下。
首先我們有n個key,bitArray的長度位m,hash函式的個數是k,失誤率是p(一般很小),推導如下:
誤判的概率:
如果hash函式足夠優秀(每一個key都等概率的分配到陣列中的某一個位置)。對於一個hash函式來說,bitArray中某個位置被置1的概率是\(\frac{1}{m}\),則不被置1的概率是\(1-\frac{1}{m}\),因為我們有k個hash函式,所以在k個hash函式中,某個位置不被置1的概率是:
\[ (1-\frac{1}{m})^k \]因為插入了n個key,某個位置置1的概率是:(不被置1的概率是\((1-\frac{1}{m})^{kn}\))
\[ 1-(1-\frac{1}{m})^{kn} \]如果我們此時去查詢某個key是否存在,出現誤判(也就是說在bitArray中k個位置都出現了1)的概率是:
\[ [1-(1-\frac{1}{m})^{kn}]^{k} \]
選擇最小的誤判概率:
根據數學知識我們知道:
\[ lim_{n\rightarrow+\infty}(1+x)^{\frac{1}{x}} = e \]
所以:
\[
[1-(1-\frac{1}{m})^{kn}]^{k} = [1-(1-\frac{1}{m})^{-m\frac{-kn}{m}}]^{k} = [1-e^{\frac{-kn}{m}}]^k
\]
然後令\(a=e^{\frac{-n}{m}}\) ,因此概率是:
\[
f(k)=(1-a^{k})^k
\]
我們需要求得便是\(f(k)\)的最小值。對\(f(k)\)進行變換求導:
\[
\begin{align}
&f(k) = (1-a^k)^k \\
&lnf(k) = kln(1-a^k) \\
&然後進行求導\\
&\frac{1}{f(k)}f'(k) = ln(1-a^k) - \frac{ka^klna}{1-a^k}\\
&\because a=e^{\frac{-n}{m}} \\
&\therefore a < 1\\
&\therefore 0< f(k)=(1-a^{k})^k <1\\
&令f'(k) = 0,則 ln(1-a^k) - \frac{ka^klna}{1-a^k} =0\\
&\therefore (1-a^k)ln(1-a^k) = ka^klna = a^kln{a^k}\\
&\therefore (1-a^k) = a^k \\
&\therefore a^k = \frac{1}{2}\\
&\therefore e^{\frac{-nk}{m}} = \frac{1}{2} \\
&\therefore \frac{nk}{m} = ln2 \\
&\therefore k = \frac{mln2}{n} = 0.7\frac{m}{n}\\
&\end{align}
\]
從上面我們可以知道,如果想讓誤判率一直維持穩定,那麼則m和n要維持線性增加。當然,如果是其他變數保持不變,也可以用上面的方法進行求出。
markdown 寫數學公式還是蠻爽的(●'◡'●)
