前言

在此記錄一些不太成熟的思考，希望對各位看官有所啟發。

從題目可以看出來這篇文章的主題很雜，這篇文章中我主要討論的是深度學習為什麼要“深”這個問題。先給出結論吧：“深”的層次結構是為了應對現實非線性問題中的複雜度，這種“深”的分層結構能夠更好地表徵影象語音等資料。

好了，如果各位看官感興趣，那就讓我們開始這次思考的旅程吧！

歸併排序

我們首先從歸併排序演算法開始，這裡先跟大家回顧一下這個演算法，相信大家都已經非常熟悉了。排序是計算機基礎演算法中的一個重要主題，要將一個無序的陣列排成有序的一個容易想到的算是冒泡法，其時間複雜度為O(n^2)，冒泡演算法並沒用到“分而治之”的思想，而是一次性地解決問題。而我們要討論的歸併演算法的時間複雜度為O(nlogn)，歸併演算法的大致原理是遞迴地將待排序的陣列分解成更小的陣列，將小陣列排好序，再逐層將這些排好序的小陣列拼成大陣列，最終完成排序。直接上程式碼吧：

def merge_sort(arr):
    """
    input : unsorted array
    output: sorted array in ascending order
    """
    if len(arr) <= 1:
        return arr
    half = len(arr)//2
    left = merge_sort(arr[0:half])
    right = merge_sort(arr[half:])
    left_tail ，right_tail = 0 ， 0
    sorted_arr = []
    while left_tail < len(left) and right_tail < len(right):
        if left[left_tail] < right[right_tail]:
            sorted_arr.append(left[left_tail])
            left_tail += 1
        else:
            sorted_arr.append(right[right_tail])
            right_tail += 1
    if left_tail < len(left):
        sorted_arr += left[left_tail:]
    else:
        sorted_arr += right[right_tail:]
    return sorted_arr
 

這段程式碼還是比較直觀吧，簡單說一下程式碼：首先確定遞迴基，即遞迴什麼時候停下來，顯然當陣列分解到只含一個數或者一個數也沒有時就停下來並將陣列返回，因為只有一個元素或沒有元素的陣列本身就是“有序”的了，所以我們直接返回。當陣列元素個數大於1個，就可以將陣列分解成左右兩個子陣列，遞迴呼叫merge_sort函式求出left 和 right 的有序陣列，後面再將有序陣列left和right合成一個大陣列返回就ok了。由於每次分解陣列的大小都在減少，會一步一步向遞迴基靠近，所以會演算法是收斂的，即一定會停下來。

這個演算法是比較基礎的演算法沒什麼好說的，但是讓我們思考一個問題，為什麼將大問題分解成小問題，這樣遞迴地倒騰一下就能將演算法複雜度從O(n^2)降為O(nlogn)?同樣的問題規模，分解了再組合的複雜度為什麼就比直接算的複雜度低？你或許可以直接用主定理(master theorem)計算出歸併演算法O（nlogn）的複雜度，但是這也不能直觀解釋我們上述的疑問。對於這個問題我們可以打個類似的比喻：10斤蘋果榨出了5斤蘋果汁，再用1斤蘋果榨汁，榨10次，其總量竟然不等於之前的不相等！

所以，這個演算法有效究竟是基於什麼邏輯？在繼續之前請好好思考一下這個問題，看各位能不能想得通。

非線性，Jensen 不等式

如果你跟我一樣都想不通上一節的問題，那你跟我可能都犯了相同的錯誤——線性思維。首先來說一下什麼是“線性”，說得學術一點就是滿足我們線性代數課本里面的那個8個法則的運算，感興趣的可以去翻一翻課本複習一下。說得稍微不嚴謹一點就是滿足“數乘”和“加法”的運算，“數乘”是說我們這個系統如果輸入翻倍其輸出也會翻倍；“加法”是說”對這個系統單獨輸入A，輸出為A_OUT,單獨輸入B輸出為B_OUT,則輸入A+B的輸出為A_OUT+B_OUT"。在說簡單點就是這個系統的輸入輸出影象是條直線或是超平面。

我們前面說的那個榨汁問題就是一個線性的系統：輸入10斤蘋果輸出為5斤蘋果汁，那麼輸入20斤蘋果輸出為10斤蘋果汁；如果輸入10斤葡萄輸出為8斤葡萄汁，那麼輸入10斤蘋果加上10斤葡萄的輸出為5斤蘋果汁和8斤葡萄汁的混合果汁。整個過程是線性的，如果我們用線性思維去思考線性系統那是ok的，一切都是合理的。但是如果我們用線性思維去思考非線性的系統那就要出問題了。回到我們那個排序問題上來，這其實是個非線性的問題，簡單的思考一下：排序20個數的工作量應該要比排2次10個數的工作量大得多。如果你不信，可以自己動手排一排去感受下。所有排序的規模與時間是非線性的，上文用一個線性的系統去做類比當然是不對的。

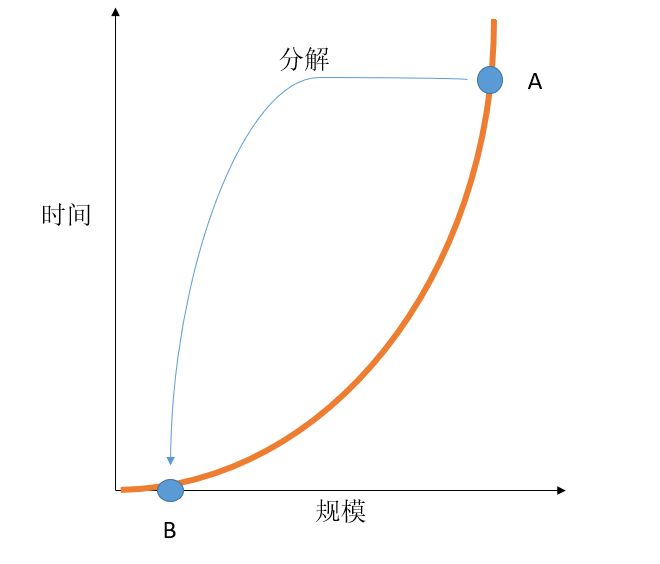
下面我們就來分析下歸併排序為什麼有效，如下圖橫軸是排序的規模，縱軸是排序的時間，我們知道，如果不將問題分解（氣泡排序），那麼時間複雜度為O(N^2)，我們用橙色曲線表示演算法規模隨時間的關係。曲線在資料規模不大的時候時間消耗並不大，甚至在規模接近0時比線性增長的時間消耗還低（此處有點不嚴謹，規模是離散的），當問題規模大到一定程度時消耗的時間才開始“起飛”。如圖中的A點，這個時候規模已經比較大了，消耗的時間也非常大。歸併排序主要思想就是將A規模的排序問題分解成若干個B規模的排序問題，“寧願解決多個簡單的B問題再將結果綜合起來也不願意解決一個複雜度很高的A問題”。正因為問題是非線性的，所以將問題分解與將問題一次解決的工作量才會不一樣。如果問題是線性無論怎樣分解其工作量是相等的。與歸併排序類似，現實生活中也有類似的非線性例子，比如學一門課需要9個小時，一天花9個小時來學，與3天每天3個小時來學的效果肯定不一樣。

下面我們進入Jenson不等式，相信你在機器學習的理論中已經接觸過了，我們來大概看一下這個不等式說了什麼。如果一個函式嚴格是嚴格下凸函式，那麼有：
\[ f(\sum_{i=1}^{N}\lambda_{i}x_{i}) < \sum_{i=1}^{N}\lambda_{i}f(x_{i}) \]
其中$ \sum_{i=1}^{N}\lambda_{i}=1$。其實下凸函式簡單的說就是曲線往下凸的非線性函式（好像是廢話，嚴格定義麻煩去翻書），凸函式其實就是非線中比較簡單的一種，仔細看看Jenson不等式，由上面這種問題分解的視角來看，這個不等式告訴我們對於凸函式，將問題分解來解決與一次性解決的結果是不相等的，並且還告訴了我們這個不相等的方向。在嚴格下凸函式中不等式左邊度量的是問題分解後的輸出；右邊是不分解的整體輸出。分解後的輸出要小於問題不分解的輸出。至於為什麼說不等式左邊是分解後的，不等式右邊是整體的，請讀者自行體會，這裡就不囉嗦了。這就是Jenson不等式，可以看成是我們之前討論的非線性問題的數學表示。

根據以上的分析我們可以看出如果演算法的時間隨規模增長是下凸函式的關係，我們都可以用歸併演算法這種“分層“的思想將問題逐層分解成更小的子問題，去解決規模較小的子問題，再回過頭來將子問題的結果合併。Jenson不等式告訴們這樣的方法比一次解決問題更省力（當然如果是上凸函式這樣分解後則更費力）。

深度學習

以上討論這些與深度學習有什麼關係？我們知道深度學習與傳統機器學習演算法的差別之一就是它中間的隱藏層數很深，像cv的resnet，nlp的bert模型層數都非常深。從理論上來說只含有一層隱藏層的神經網路，只要這一層的神經元足夠多就能以任意誤差擬合任意函式。所以理想情況下，即資料足夠多足夠好的情況下，這種只有一層的神經網路也能夠工作得很好，比如SVM就可以看成是隻有一個隱藏層的模型，這麼看來只要資料足夠多就沒有深度學習什麼事了？但是現實情況下正是深度學習這種“深”層次的表徵才讓深度學習脫穎而出，效能超過各種淺層模型。我們之前說的資料足夠多足夠好的理想情況太過烏托邦，現實中資料，算力總是不足的，因此尋求對於資料更高效的表徵比尋找一個烏托邦的方法更為實際。這種烏托邦的例子我還可以舉一個，比如我曾經認為只要我們研究透徹了量子力學，則可以推出其他所有學科的結論，比如化學、生物、社會學。是的，的確只要有足夠的算力足夠的時間和耐心一定可以由量子力學推匯出其他學科。但是這太理想話，用量子力學去推導生物學其複雜度與工作量可想而知，我們沒有人有這樣的精力去做這種工作。所以我們要將問題分層，在不同層次上去解決問題，從而降低問題的複雜度，所以量子力學的突破並不會讓化學、生物這這些學科消失，不同學科它們各自需要解決的問題。再舉一個例子，我們的程式語言也是分層次的，比如有接近硬體的彙編、c語言，有高階點的c++、java、python等，以及更高層次的各種程式設計框架與函式庫，理論上說用底層的組合語言也可以實現一切，但是問題還是一個複雜度的問題，不同的語言關注不同的問題。試想用匯編語言去編寫一個3D遊戲其難度如何？

說了這麼多，現在說回深度學習，深度學習就是採用分層的思想將一個複雜的問題分解成不同的層次去解決，比如一個圖片分類的神經網路，低層的網路去識別線條、邊角等特徵，高一點的層次識別圓形、方形等幾何特徵，再高的層次識別人、飛機、動物等更抽象的特徵。至於說為什麼的這樣的分層有效，我覺得其實跟之前介紹的歸併演算法有效的原理以及Jensen不等式的原理其實是一樣的。深度學習擅長的影象識別、語音識別這類問題的規模與複雜度之間其實也可以近似看成下凸的，之前的分析可以知道這種下凸的問題採用逐層分解子問題的方式能夠有效降低複雜度。深度學習不僅能採用分層的方式設計模型，還能用反向傳播演算法自動求解各個層次的引數，這正是這種方法的奇妙之處，現實已經證明了這種方法的有效性。可以說深度學習這種分層表徵資料的結構是對影象、語音、文字類資料的高效表徵。當然上面的分析過於簡單，現實中資料複雜的非線性可能非常複雜，而不僅僅能用一個“凸“的性質描述，所以對於不同的問題需要探索不同的模型結構。

總結

這篇部落格中我們簡單地介紹了歸併演算法，分析了這種將問題分層處理的方式為什麼會高效，接著介紹了jenson不等式，並分析了對於凸性函式將輸入分解和整體處理輸出的大小關係，接著我們從這個角度分析了深度學習演算法為什麼要“深”：因為這種深度的分層結構是對“下凸”的問題的一種高效的表徵。

這篇部落格不太嚴謹，歡迎拍