共軛梯度法求解協同過濾中的 ALS
協同過濾是一類基於使用者行為資料的推薦方法,主要是利用已有使用者群體過去的行為或意見來預測當前使用者的偏好,進而為其產生推薦。能用於協同過濾的演算法很多,大致可分為:基於最近鄰推薦和基於模型的推薦。其中基於最近鄰推薦主要是通過計算使用者或物品之間的相似度來進行推薦,而基於模型的推薦則通常要用到一些機器學習演算法。矩陣分解可能是被研究地最多的基於模型的推薦演算法,在著名的 Netflix 大賽中也是大放異彩,核心思想是利用低維隱向量為每個使用者和物品建模,進而推測使用者對物品的偏好。現在的關鍵問題是如果要用矩陣分解的方法,該如何訓練模型,即該如何獲得隱向量? 目前主流的方法有兩種:隨機梯度下降 (簡稱 SGD,stochastic gradient decent) 和交替最小二乘法 (簡稱 ALS,alternating least squares),而本文的重點是後者,在闡述其基本原理的同時,引入共軛梯度法來加速模型的訓練。
矩陣分解想要解決的問題
這裡採用最常見的矩陣分解技術,由 SVD 演化而來。設共有 \(m\) 個使用者,\(n\) 個物品,那麼使用者 - 物品 - 評分矩陣為 \(R \in \mathbb{R}^{m \times n}\) ,其中評分表示使用者對物品的偏好。這個矩陣通常非常稀疏,其中大部分的評分元素都是缺失的,而我們的任務就是預測裡面的缺失值。對於每個使用者 \(u\) 設定一個使用者向量 \(x_u \in \mathbb{R}^f\) ,每個物品 \(i\) 設定一個物品向量 \(y_i \in \mathbb{R}^f\) ,那麼預測值用二者的內積表示 \(\hat{r}_{ui} = x_u^{\top}y_i\) 。於是可寫出想要優化的目標函式:
\[
\mathcal{L} \;=\; \min_{x_*,y_*} \sum\limits_{r_{u,i}\,\text{is}\,\text{known}} (r_{ui} - x_u^\top y_i)^2 + \lambda \left(\sum\limits_{u}||x_u||^2 + \sum\limits_{i}||y_i||^2 \right) \tag{1.1}
\]
想要最小化 \((1.1)\) 式最常用的方法就是 SGD (其中 \(\gamma\) 是學習率):
\[
e_{ui} \overset{def}{=} r_{ui} - x_u^\top y_i \\[1ex]
x_u \leftarrow{x_u + \gamma \,(e_{ui} \cdot y_i - \lambda \cdot x_u)} \\[1ex]
y_i \leftarrow{y_i + \gamma \,(e_{ui} \cdot x_u - \lambda \cdot y_i)}
\]
SGD 是一種迭代優化方法 (iterative method),而另一種方法,即本文的主角 ALS ,則是一種直接法 (direct method)。由於 \((1.1)\) 式中 \(x_u\) 和 \(y_i\) 都未知,所以該函式非凸,難以直接優化。然而如果將所有的 \(y_i\) 固定住視其為常數,那麼 \((1.1)\) 式就變成了一個 關於 \(x_u\) 的最小二乘問題,可以直接求出解析解。於是可以先固定 \(y_i\) 求出 \(x_u\) ,再固定 \(x_u\) 求出 \(y_i\) ,二者不斷交替,這個流程不斷重複直至收斂。因而 ALS 全稱為交替最小二乘法 (alternating least squares),這其實有點類似於 EM 演算法中 E 步和 M 步的交替求解。
下面詳細推導 ALS 的演算法流程,上面已經定義了使用者向量 \(x_u \in \mathbb{R}^f\) ,物品向量 \(y_i \in \mathbb{R}^f\) ,則所有使用者可組合成一個矩陣 \(X \in \mathbb{R}^{m \times f}\) ,所有物品組合成一個矩陣 \(Y \in \mathbb{R}^{n \times f}\) ,整個評分矩陣為 \(R = XY^\top \in \mathbb{R}^{m \times n}\) 。則對 \((1.1)\) 式固定 \(Y\) 對 \(x_u\) 求偏導:
\[
\begin{align*}
\frac{\partial \mathcal{L}}{\partial\,x_u} &= -2\sum\limits_{i \in r_{u*}} (r_{ui} - x_u^\top y_i)y_i + 2 \lambda\, x_u = 0 \quad \implies \\
x_u &= \left(\sum\limits_{i \in r_{u*}} y_i y_i^\top + \lambda\, I\right)^{-1} \sum\limits_{i \in r_{u*}}r_{ui}y_i = (Y_u^\top Y_u + \lambda \,I)^{-1}Y_u^\top R_u \tag{1.2}
\end{align*}
\]
其中 \(r_{u*}\) 表示使用者 \(u\) 評分過的所有物品, \(Y_u \in \mathbb{R}^{|r_{u*}| \times f}\) 表示使用者 \(u\) 評分過的所有物品的矩陣,\(R_u \in \mathbb{R}^{|r_{u*}|}\) 表示使用者 \(u\) 所有的物品評分向量。同理固定 \(X\) 對 \(y_i\) 求偏導:
\[
y_i = \left(\sum\limits_{u \in r_{*i}} x_u x_u^\top + \lambda\, I\right)^{-1} \sum\limits_{u \in r_{*i}}r_{ui}x_u = (X_i^\top X_i + \lambda \,I)^{-1}X_i^\top R_i \tag{1.3}
\]
ALS 相對於 SGD 有兩個好處:
(1) 注意到 \((1.2)\) 和 \((1.3)\) 式每個 \(x_u\) 和 \(y_i\) 的計算都是獨立的,因而可以平行計算提高速度。
(2) 對於隱式反饋資料集來說,使用者和物品的組合太多,分分鐘到億級別。若有10000個使用者,10000個物品,則會有 \(10000 \times 10000 = 10^8\) 種組合,用 SGD 一個個迭代是比較困難的。當然也可以為每個使用者進行少量負取樣,但這不是本文的重點,在此略過。而用 ALS 則可以通過一些矩陣轉換技巧來高效計算,不過在這之前,先來看下何為隱式反饋資料集?
顯式反饋 Vs. 隱式反饋
上文 ALS 的推導使用的是顯式反饋資料,特點是都有顯式評分,比如 MovieLens 資料集中的 1-5 分或是豆瓣上的 1 到 5 星。這些評分很能反映使用者對物品的偏好,像豆瓣上打 5 星表示力薦,打 1 星表示很差。相較而言,隱式反饋資料大都來源於使用者的行為,如物品的購買記錄,網頁的瀏覽記錄,視訊的觀看時長等等。隱式反饋一般有如下特點:
(1) 資料總量大。比如很多人都在淘寶上買東西留下記錄,卻很少人會去給好評差評;每天在網上瀏覽了很多文章,卻很少點贊。
(2) 沒有負反饋。這點是比較致命的,比如看過一部電影代表對其的偏好,但若沒看過一部電影並不代表不喜歡這部電影,可能是在待觀看列表裡面,然而從資料中這一點無法得知,這導致資料的噪音大。而如果只用有反饋的資料進行建模,會導致嚴重的過擬合。
如上面第一點所述,實際生活中顯式反饋的評分資料是比較少的,而隱式反饋資料卻非常豐富,因而重要性越來越高。為了解決其沒有負反饋的問題,這裡採用 Hu 等人在論文《Collaborative Filtering for Implicit Feedback Datasets》中描述的方法,引入使用者對於物品的偏好係數 \(p_{ui}\) :
\[
p_{ui} =
\begin{cases}
\;1 \quad \text{if}\;\; r_{ui} > 0 \\
\;0 \quad \text{if}\;\; r_{ui} = 0
\end{cases}
\]
\(r_{ui}\) 表示使用者對物品的反饋,如購買、搜尋等行為,上式表明只要有反饋,\(p_{ui}\) 皆為 \(1\) 。此外還引入使用者對於物品的置信度 $c_{ui} = 1 + \alpha, r_{ui} $, 可以看出即使 \(r_{ui} = 0\) ,\(c_{ui}\) 也不為零,並且隨著 \(r_{ui}\) 的增長而增長。Hu 的論文中的場景是電視劇推薦,因而 \(r_{ui}\) 表示觀看時長或收看次數。於是寫出目標函式:
\[
\mathcal{L}_\text{implicit} \;=\; \min_{x_*,y_*} \sum\limits_{u,i} c_{ui}\left(p_{ui} - x_u^\top y_i \right)^2 + \lambda \left(\sum\limits_{u}||x_u||^2 + \sum\limits_{i}||y_i||^2 \right) \tag{1.4}
\]
\((1.4)\) 和 \((1.1)\) 式雖然長得很像,但實際使用會有很大區別,\((1.1)\) 式僅考慮使用者評過分的樣本,而 \((1.4)\) 式是考慮所有使用者和物品的組合,比如 MovieLens 1M 資料集有100萬樣本,6000個使用者,3500部電影,總的組合數是 \(6000 \times 3500 = 2.1 \times 10 ^7\) ,是樣本數的 21 倍,如果用 SGD 那將會比顯式資料集慢很多。
另外仔細觀察 \((1.1)\) 式,固定所有的 \(y_i\) ,求解最優的 \(x_u\) ,從形式上來說就是一個 Ridge Regression 問題,因而 \((1.4)\) 式相當於為每個使用者 - 物品組合加上了權重 \(c_{ui}\),因而該演算法也被稱為 WRR (weighted ridge regression) 。
要優化 \((1.4)\) 式,還是 ALS 的思路,固定 \(Y\) 對 \(x_u\) 求偏導:
\[
\begin{align*}
\frac{\partial \mathcal{L}_\text{implicit}}{\partial\, x_u} &= -2\sum\limits_{u,i} c_{ui}(p_{ui} - x_u^\top y_i)y_i + 2 \lambda\, x_u = 0 \quad \implies \\
x_u &= \left(\sum\limits_{u,i} c_{ui}y_iy_i^\top + \lambda\,I\right)^{-1}\sum\limits_{u,i} c_{ui}p_{ui}y_i \tag{1.5} \\[1ex]
&= (Y^\top C^uY + \lambda \,I)^{-1}Y^\top C^up(u) \tag{1.6}
\end{align*}
\]
其中 \(Y \in \mathbb{R}^{n \times f}\) 為所有物品隱向量組成的矩陣,\(C^u \in \mathbb{R}^{n \times n}\) 為對角矩陣,其對角線上的元素為使用者 \(u\) 對所有物品的置信度 \(c_{ui}\),即 \(C^u_{ii} = c_{ui}\) ,由上文可知因為 \(r_{ui} \geqslant 0\) ,所以 \(c_{ui} \geqslant 1\)。\(p(u) \in \mathbb{R}^n\) ,其元素為使用者 \(u\) 對所有物品的偏好 \(p_{ui}\) 。
\((1.6)\) 式中的 \(Y^\top C^u Y\) 的計算複雜度達到了 \(\mathcal{O}(f^2n)\) ,在 \(n\) 很大的情況下是難以承受的,因而可以拆分成 \(Y^\top C^u Y = Y^\top Y + Y^\top (C^u - I)Y\),對於每個使用者 \(u\) 來說, \(Y^\top Y\) 都是一樣的,因而可以提前計算,而 \(C^u\) 對角線的元素大部分都為 \(1\) ,因而 \(C^u - I\) 是一個稀疏矩陣,整體 \(Y^\top C^u Y\) 的計算複雜度降到 \(\mathcal{O}(f^2n_u)\),\(n_u\) 是使用者 \(u\) 產生過行為的物品數量,通常 \(n_u << n\) 。
同理,固定 \(X\) 對 \(y_i\) 求偏導得:
\[
\begin{align*}
y_i &= \left(\sum\limits_{u,i} c_{ui}x_u x_u^\top + \lambda\,I\right)^{-1}\sum\limits_{u,i} c_{ui}p_{ui}x_u \\[1ex]
&= (X^\top C^{\,i} X + \lambda \,I)^{-1} X^\top C^{\,i} p(i)
\end{align*}
\]
下面給出 \((1.6)\) 式的 Python 程式碼:
import numpy as np
from scipy.sparse import csr_matrix
def ALS(dataset, X, Y, reg, n_factors, alpha=10, user=True):
if user:
data = dataset.train_user # data是所有使用者-物品-標籤的巢狀字典,形如 {1:{2:1, 3:1, 5:1 ...}, 2: {2:1, 3:1 ...} ...}
m_shape = dataset.n_items
else:
data = dataset.train_item # data是所有物品-使用者-標籤的巢狀字典
m_shape = dataset.n_users
YtY = Y.T.dot(Y) + reg * np.eye(n_factors)
for s in data:
Cui_indices = list(data[s].keys())
labels = list(data[s].values())
Cui_values = np.array(labels) * alpha
Cui = csr_matrix((Cui_values, (Cui_indices, Cui_indices)), shape=[m_shape, m_shape]) # 構建 C^u - I 稀疏矩陣
pui_indices = list(data[s].keys())
pui = np.zeros(m_shape)
pui[pui_indices] = 1.0
A = YtY + np.dot(Y.T, Cui.dot(Y))
C = Cui + sparse.eye(m_shape, format="csr")
cp = C.dot(pui)
b = np.dot(Y.T, cp)
X[s] = np.linalg.solve(A, b)
另外根據 \((1.5)\) 式也可以拆分成 :
\[
\begin{align*}
x_u &= \left(\sum\limits_{u,i} c_{ui}y_iy_i^\top + \lambda\,I\right)^{-1} \sum\limits_{u,i} c_{ui}p_{ui}y_i \\[1ex]
&= \left(\sum\limits_{u,i} y_iy_i^\top + \sum\limits_{u,i} \left(c_{ui} - 1\right)y_iy_i^\top + \lambda\,I\right)^{-1} \sum\limits_{u,i} c_{ui}p_{ui}y_i \qquad \#\; 對於 p_{ui} = 0 的物品,c_{ui}-1=0 \\[1ex]
&= \left(Y^\top Y + \sum\limits_{i \in r_{u*}} \left(c_{ui} - 1\right)y_iy_i^\top + \lambda\,I\right)^{-1} \sum\limits_{i \in r_{u*}} c_{ui}\cdot1 \cdot y_i \qquad\qquad\qquad\qquad\qquad\qquad\qquad (1.7)
\end{align*}
\]
所以還有另一種程式碼更少且更快的實現方式:
def ALS(dataset, X, Y, reg, n_factors, alpha=10, user=True):
if user:
data = dataset.train_user
else:
data = dataset.train_item
YtY = Y.T.dot(Y)
for s in data:
A = YtY + reg * np.eye(n_factors)
b = np.zeros(n_factors)
for i in data[s]:
factor = Y[i]
confidence = 1 + alpha * data[s][i]
A += (confidence - 1) * np.outer(factor, factor) # 計算外積
b += confidence * factor
X[s] = np.linalg.solve(A, b)
假設 \((Y^\top C^uY + \lambda \,I)^{-1}\) 的矩陣求逆操作複雜度為 \(\mathcal{O}(f^3)\),那麼所有使用者 \(u\) 的總體計算複雜度為 \(\mathcal{O}(f^2 \mathcal{N}_u + f^3m)\) ,其中 \(\mathcal{N}_u = \sum_un_u\) ,為所有使用者行為總量。可以看出該演算法的計算複雜度雖然與總體資料量呈線性增長關係,然而會隨著 \(f\) 的增加呈指數增長。 總之雖然比原來有改善但其實還是比較慢,所以接下來就輪到共軛梯度法出場了,但在此之前,先來看看傳統的梯度下降法有什麼問題。
梯度下降法的問題
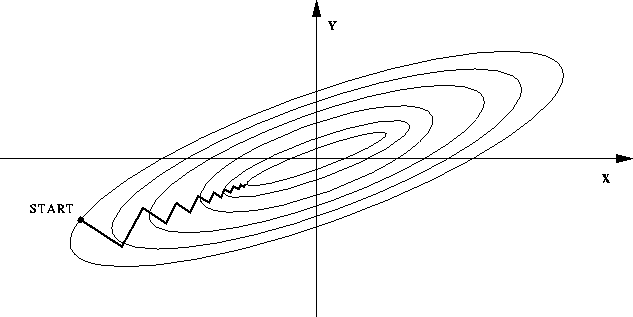
我們的目標是最小化 \((1.4)\) 式,使得推薦結果和真實值越接近越好,傳統的梯度下降法有兩個缺點: 一是資料量大時迭代慢,二是函式等高線呈橢球面時,容易呈現一種來回震盪的趨勢。下圖顯示出一種典型的“之字形”優化路徑,同樣的迭代方向可能不只走了一次,這造成了優化效率低下。
而比較理想的情況應該是這樣,每一步的搜尋方向都向最優點的方向靠攏:
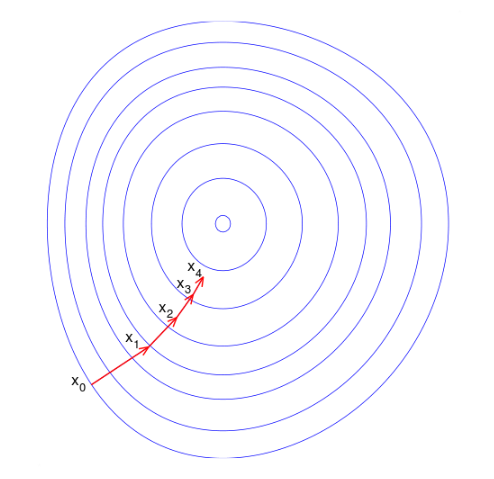
因此很自然的想法是,能不能找一組 n 個迭代方向,每次沿著一個方向只走一次達到該方向的最優解,那麼最多走 n 次就能收斂到最優解了。這種方法究竟有沒有呢?當然是有的(汗,要是沒有我寫這篇文章還有什麼意義。。),就是共軛梯度法嘛。
共軛梯度法 (conjugate gradient)
共軛梯度法天性適合求解大規模稀疏線性方程組問題,而本文中的矩陣分解恰好可轉化為這一類問題。首先來看什麼是“共軛”,設 \(\boldsymbol{A}\) 為對稱正定矩陣,對於兩個非零向量 \(\boldsymbol{u}\) 和 \(\boldsymbol{v}\) ,若 \(\boldsymbol{u}^\top \boldsymbol{A} \boldsymbol{v} = 0\) ,則稱 \(\boldsymbol{u}\) 和 \(\boldsymbol{v}\) 關於 \(\boldsymbol{A}\) 共軛。對於 \(n\) 維二次型函式 \(f(\boldsymbol{x}) = \frac12 \boldsymbol{x^\top A x} - \boldsymbol{x^\top b}\) ,\(\boldsymbol{x} \in \mathbb{R}^n\) ,最好的迭代方向為關於 \(\boldsymbol{A}\) 的共軛方向,每次迭代其中一個方向,那麼最多 \(n\) 步之後就能到達最優點。
於是剩下的問題是如何得到一組關於 \(\boldsymbol{A}\) 的共軛方向? 所謂的共軛梯度法可理解為 “共軛方向 + 梯度 $\Longrightarrow $ 新共軛方向” ,這樣就避免了需要預先給定一組共軛方向,而是每一輪迭代中根據上一輪共軛向量和梯度的線性組合來確定新方向,這樣就節約了很多空間。
對於上述的二次型函式,其梯度為 \(\nabla f(\boldsymbol{x}) = \boldsymbol{Ax} - \boldsymbol{b}\) ,若令其為零則等價於求方程 \(\boldsymbol{Ax} = \boldsymbol{b}\) 的解。在上文 ALS 演算法中是直接矩陣求逆得 \(\boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b}\) ,而共軛梯度法作為一種迭代方法來說,設第 \(k\) 步的搜尋方向為 \(\boldsymbol{p}_k\) ,則第 \(k + 1\) 步的解為 \(\boldsymbol{x}_{k+1} = \boldsymbol{x}_k + \alpha_k \boldsymbol{p}_k\) 。新的共軛方向為上一輪共軛方向和負梯度的線性組合,即 \(\boldsymbol{p}_{k+1} = - \nabla f( \boldsymbol{x} ) + \beta_k \boldsymbol{p}_k\) 。設殘差 \(\boldsymbol{r} = \boldsymbol{b} - \boldsymbol{A x}\) ,則對於二次型函式 \(f(\boldsymbol{x})\) 來說,負梯度就是殘差,則 \(\boldsymbol{p}_{k+1} = \boldsymbol{r}_k + \beta_k \boldsymbol{p}_k\) 。而對於新一輪的殘差: \(\boldsymbol{r}_{k+1} = \boldsymbol{b} - \boldsymbol{A}\boldsymbol{x}_{k+1} = \boldsymbol{b} - \boldsymbol{A}(\boldsymbol{x}_k + \alpha_k \boldsymbol{p}_k) = \boldsymbol{r}_k - \alpha_k \boldsymbol{Ap}_k\) 。於是完整的共軛梯度法如下所示:

\(\boldsymbol{p}\) 即為每一輪的共軛搜尋方向,其初始方向依據梯度下降法設定為梯度的負方向,即殘差 \(\boldsymbol{p}_0 = \boldsymbol{r}_0\)。由 \(\boldsymbol{x} = \boldsymbol{A}^{-1} \boldsymbol{b}\) ,那麼根據 \((1.6)\) 和 \((1.7)\) 式:
\[
\begin{align*}
\boldsymbol{A} &= Y^\top C^uY + \lambda \,I = Y^\top Y + \sum\limits_{i \in r_{u*}} \left(c_{ui} - 1\right)y_iy_i^\top + \lambda\,I \\[1ex]
\boldsymbol{b} &= Y^\top C^up(u) = \sum\limits_{i \in r_{u*}} c_{ui}\cdot1 \cdot y_i \\[1ex]
\boldsymbol{r} &= \boldsymbol{b} - \boldsymbol{Ax} = \sum\limits_{i \in r_{u*}}\left(c_{ui} - (c_{ui} - 1)y_i^\top x\right)\cdot y_i - (Y^\top Y + \lambda\,I)^\top x
\end{align*}
\]
下面給出共軛梯度法的實現程式碼:
def conjugate_gradient(dataset, X, Y, reg, n_factors, alpha=10, cg_steps=3, user=True):
if user:
data = dataset.train_user
else:
data = dataset.train_item
YtY = Y.T.dot(Y) + reg * np.eye(n_factors)
for s in data:
x = X[s]
r = -YtY.dot(x)
for item, label in data[s].items():
confidence = 1 + alpha * label
r += (confidence - (confidence - 1) * Y[item].dot(x)) * Y[item] # b - Ax
p = r.copy()
rs_old = r.dot(r)
if rs_old < 1e-10:
continue
for it in range(cg_steps):
Ap = YtY.dot(p)
for item, label in data[s].items():
confidence = 1 + alpha * label
Ap += (confidence - 1) * Y[item].dot(p) * Y[item]
# standard CG update
alpha = rs_old / p.dot(Ap)
x += alpha * p
r -= alpha * Ap
rs_new = r.dot(r)
if rs_new < 1e-10:
break
p = r + (rs_new / rs_old) * p
rs_old = rs_new
X[s] = x完整程式碼可見推薦系統庫 LibRecommender 中的實現 。
從計算效率上來看,共軛梯度法介於梯度下降法和牛頓法之間,克服了梯度下降法收斂慢的問題,也避免了牛頓法需要計算 Hessian 矩陣的缺點。其計算複雜度為 \(\mathcal{O}(\mathcal{N}_u\, E)\) ,空間複雜度為 \(\mathcal{O}(\mathcal{N}_u)\), 其中\(E\) 為迭代次數,而 \(\mathcal{N}_u = \sum_un_u\) ,為所有使用者行為總量, 通常每個使用者只對少量的物品產生行為,因而可以看到共軛梯度法充分利用了資料的稀疏性,提高了計算效率。
上文提到共軛梯度法最多在 \(n\) 步內即可收斂,然而對於高維資料 (超過百萬維的資料並不鮮見) 而言,這依然不能讓人滿意。不過可以證明,若正定矩陣 \(\boldsymbol{A}\) 有 \(i\) 個不同的特徵值,那麼共軛梯度法最多可在 \(i\) 步內收斂,這樣又大大提高了優化效率。下面使用 MovieLens 1m 資料集進行測試,並與傳統的 ALS 進行比較,\(f\) 統一設為 \(100\), 評估指標為 ROC 下 AUC,下圖顯示共軛梯度法在迭代 3 步後就已經接近收斂了 (注: 這裡的 3 步指的是一個 epoch 內的迭代步數,而非 3 個 epoch):
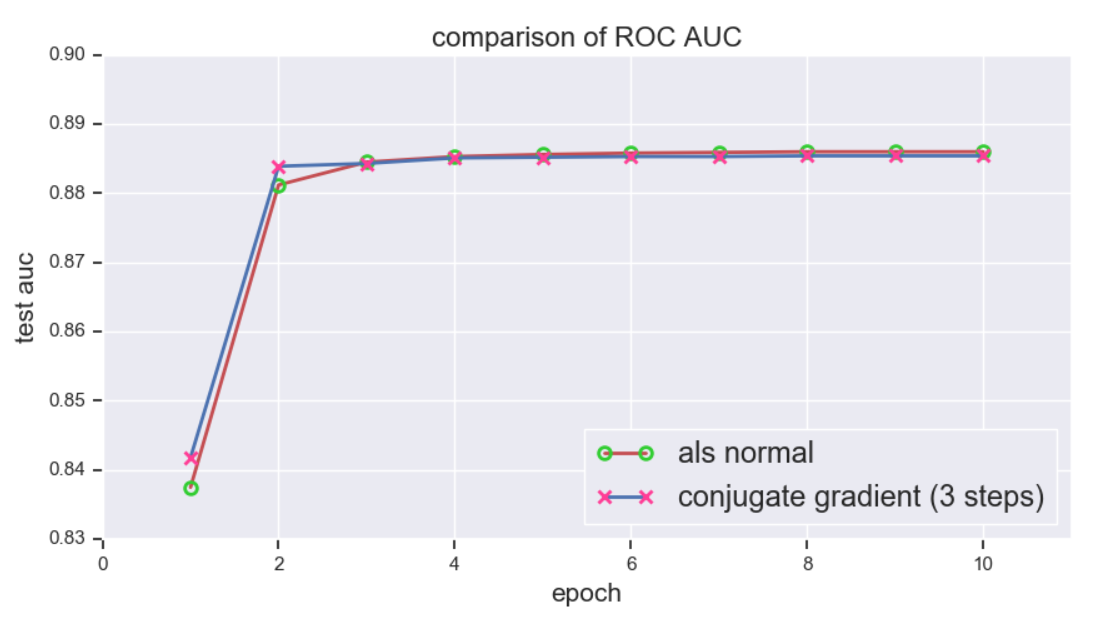
接下來對比訓練速度,共軛梯度法展現出驚人的速度,隨著 \(f\) 的增長訓練時間幾乎不變,而相比之下傳統 ALS 的訓練時間增長神速,可見 \(f\) 越大,提升越明顯: