非確定的自動機NFA確定化為DFA
摘要:
在編譯系統中,詞法分析階段是整個編譯系統的基礎。對於單詞的識別,有限自動機FA是一種十分有效的工具。有限自動機由其對映f是否為單值而分為確定的有限自動機DFA和非確定的有限自動機NFA。在非確定的有限自動機NFA中,由於某些狀態的轉移需從若干個可能的後續狀態中進行選擇,故一個NFA對符號串的識別就必然是一個試探的過程。這種不確定性給識別過程帶來的反覆,無疑會影響到FA的工作效率。因此,對於一個非確定的有限自動機NFA M,經常的做法是構造一個確定的有限自動機DFA M’。
有窮自動機(也稱有限自動機)作為一種識別裝置,能準確地識別正規集,即識別正規文法所定義的語言和正規式所表示的集合。引入有窮自動機理論,正是為詞法分析程式的自動構造尋找特殊的方法和工具。
NFA轉換為等價的DFA:在有窮自動機的理論裡,有這樣的定理:設L為一個由不確定的有窮自動機接受的集合,則存在一個接受L的確定的有窮自動機。這裡不對定理進行證明,只介紹一種演算法,將NFA轉換成接受同樣語言的DFA,這種演算法稱為子集法。寶閥為一個NFA構造相應的DFA的基本想法是讓DFA的每一個狀態對應NFA的一組狀態。也就是讓DFA使用它的狀態去記錄在NFA讀入一個輸入符號後可能達到的所有狀態,在讀入輸入符號串a1
題目:
1.設有 NFA M=( {0,1,2,3}, {a,b},f,0,{3} ),其中 f(0,a)={0,1} f(0,b)={0} f(1,b)={2} f(2,b)={3}
畫出狀態轉換矩陣,狀態轉換圖,並說明該NFA識別的是什麼樣的語言。
| a | b | |
| 0 | 0,1 | 0 |
| 1 | 2 | |
| 2 | 3 | |
| 3 |
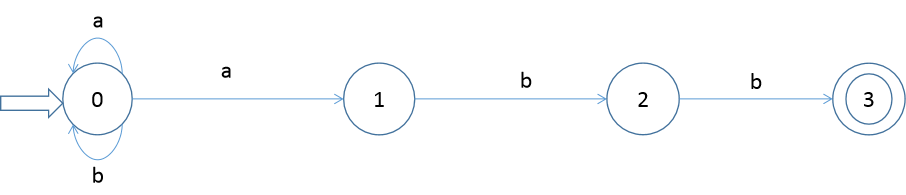
語言:(a | b)*abb
2.NFA 確定化為 DFA
1.解決多值對映:子集法
1). 上述練習1的NFA
| a | b | ||
| A | {0} | {0,1} | {0} |
| B | {0,1} | {0,1} | {0,2} |
| C | {0,2} | {0,1} | {0,3} |
| D | {0,3} | {0,1} | {0} |
DFA圖:
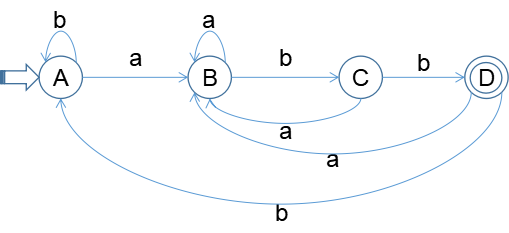
2). P64頁練習3

DFA狀態轉換矩陣
| 0 | 1 | ||
| A | {S} | {V,Q} | {Q,U} |
| B | {V,Q} | {Z,V} | {Q,U} |
| C | {Q,U} | {V} | {Q,U,Z} |
| D | {V} | {Z} | |
| E | {Z,V} | {Z} | {Z} |
| F | {Q,U,Z} | {Z} | {Q,Z} |
| G | {Z} | {Z} | {Z} |
| H | {Q,Z} | {Z} | {Q,Z} |
DFA圖:
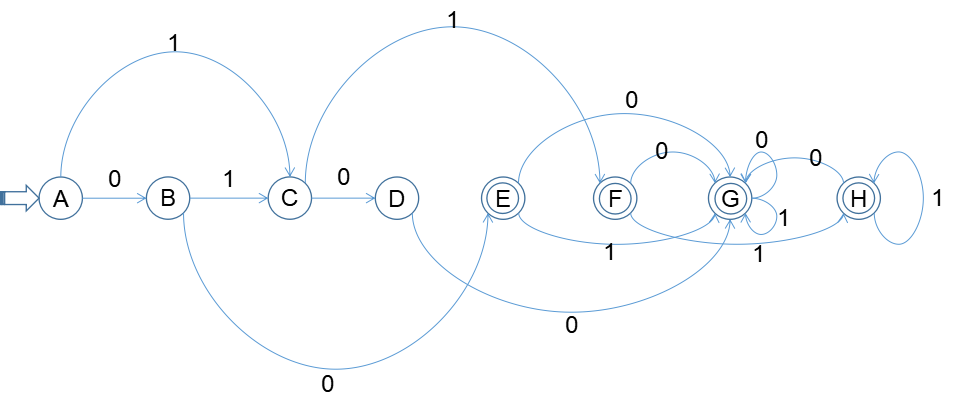
2.解決空弧:對初態和所有新狀態求ε-閉包
1). 發給大家的圖2
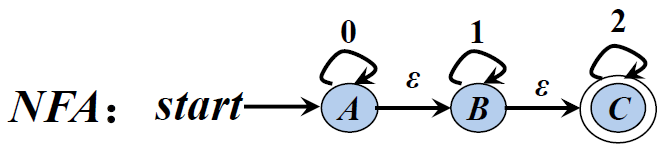
DFA狀態轉換矩陣
| 0 | 1 | 2 | ||
| X | ε{A}={ABC} | ε{A}={ABC} | ε{B}={BC} | ε{C}={C} |
| Y | ε{BC} | ε{B}={BC} | ε{C}={C} | |
| Z | ε{C} | ε{C}={C} |
DFA圖:
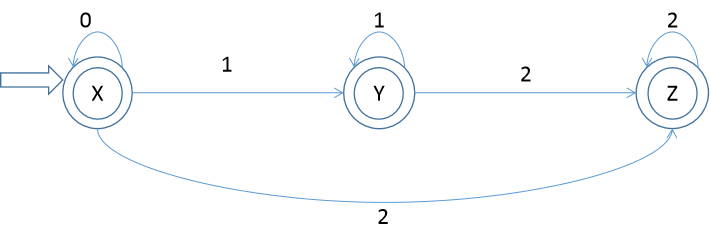
語法:(0*11* | 0*)22*
2).P50圖3.6
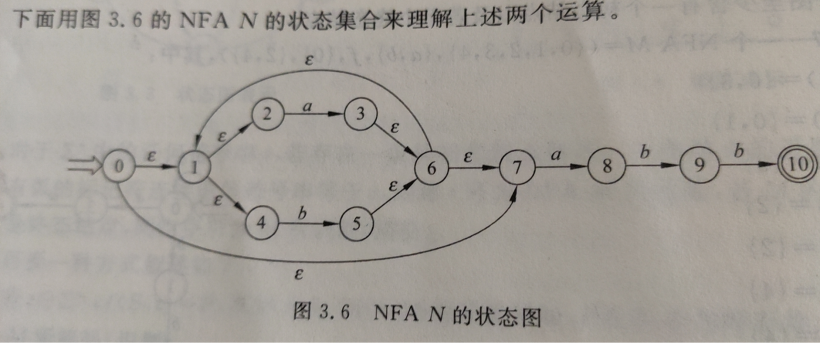
DFA狀態轉換矩陣
| a | b | ||
| 0 | ε{0}={01247} | ε{38}={3671248} | ε{5}={567124} |
| 1 | ε{1234678} | ε{38}={1234678} | ε{59}={5671249} |
| 2 | ε{124567} | ε{38}={3671248} | ε{5}={567124} |
| 3 | ε{1245679} | ε{38}={3671248} | ε{510}={56712410} |
| 4 | ε{12456710} | ε{38}={3671248} | ε{5}={567124} |
DFA圖:

子集法:
f(q,a)={q1,q2,…,qn},狀態集的子集
將{q1,q2,…,qn}看做一個狀態A,去記錄NFA讀入輸入符號之後可能達到的所有狀態的集合。
步驟:
1).根據NFA構造DFA狀態轉換矩陣
①確定DFA的字母表,初態(NFA的所有初態集)
②從初態出發,經字母表到達的狀態集看成一個新狀態
③將新狀態新增到DFA狀態集
④重複23步驟,直到沒有新的DFA狀態
2).畫出DFA
3).看NFA和DFA識別的符號串是否一
