上篇部落格我們說了感知器，這篇部落格主要記錄自適應線性神經元的實現演算法及一些其他的訓練細節，自適應線性神經元（簡稱為Adaline）由Bernard Widrow和他的博士生Tedd Hoff提出，對感知器演算法進行了改進。

當然Adaline對輸入向量x的處理和感知器是一樣的，都是使用一個權重向量w與x線性組合後得到z，再使用啟用函式將z壓縮到二元輸入（1/-1），區別在於Adaline使用梯度下降法來更新w。

因為我們的目的是準確分類，那麼我們需要來衡量分類效果的好壞，在這裡我們介紹目標函式：
\[ J(w) = \frac12 \sum_i^n(y^i - \phi(z^i))^2 \]
它也可以叫做損失函式，通過上式我們可以大致理解為什麼叫做損失函式，此函式可以計算出所有訓練樣本的真實值和預測值之間的誤差平方和（Sum of Squared Errors，簡稱SSE），式子前面的那個1/2是為了之後求導方便新增的，沒有其他意義。

有了損失函式，於是我們的目的更具體一點，就是為了選擇合適的w，使損失函式取得最小值，損失函式越小，就意味著錯誤分類的情況越少，演算法的分類效果也就越好。而因為Adaline的損失函式是一個凸函式，所以我們可以使用梯度下降來找到使損失函式取值最小的權重向量w，我們可以想象為一個小球滾下山：

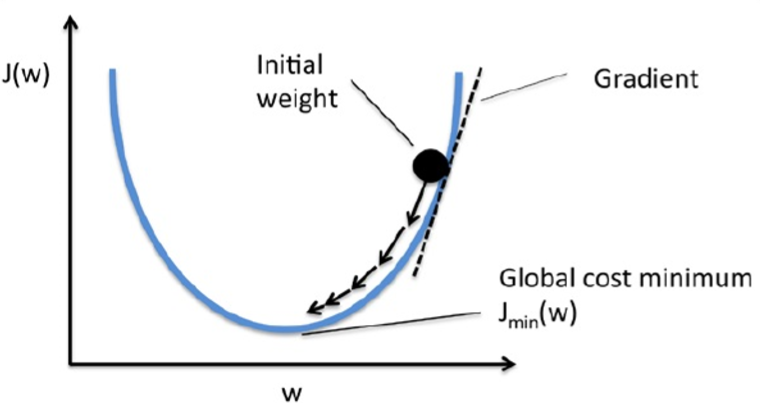
剛開始的w也許會得到一個很大的損失函式，但是由於損失函式J是w的函式，並且也是一個凸函式，它存在一個最小值，學過微積分的朋友應該知道，要找到一個函式的最值，一般的方法通過求導並使導數為零，解出的那個x就是最值，在這裡的梯度下降也就是求導，但由於w是一個權重向量，是多維的，所以需要損失函式對w求偏導，得到w中每個分量的偏導數，然後再更新整個w，具體的推導過程如下：
\[ 注意：w為向量，w_j為向量w中的某一分量\\w = w + \Delta w\\\Delta w = -\eta\Delta J(w)\\\frac{\partial J}{\partial w_j} = \frac{\partial }{\partial w_j} \frac 12 \sum_i(y^i-\phi(z^i))^2 \\= \frac 12 \frac{\partial }{\partial w_j} \sum_i(y^i-\phi(z^i))^2 \\= \frac 12 \sum_i2(y^i-\phi(z^i)) \frac{\partial }{\partial w_j}(y^i-\phi(z^i))\\= \sum_i(y^i-\phi(z^i))\frac{\partial }{\partial w_j}(y^i-\sum_i(w_j^ix_j^i))\\=\sum_i(y^i-\phi(z^i))(-x_j^i)\\=-\sum_i(y^i-\phi(z^i))x_j^i\\所以\Delta w_j = -\eta\frac{\partial J}{\partial w_j}=\eta\sum_i(y^i-\phi(z^i))x_j^i \]
一點要注意所以的權重向量w中的分量是同時更新的，而且每次更新都用到了所有的訓練樣本，所以梯度下降法也被稱為批量梯度下降（batch gradient descent）

接下來我們具體來實現自適應線性神經元，由於和感知機的學習規則很相似，所以直接在感知器的基礎上進行修改得到，其中需要修改fit方法，因為在這裡我們要使用梯度下降演算法。

class AdalineGD(object):
    """ADAptive LInear NEuron classifier.

    Parameters
    ----------
    eta:float
        Learning rate(between 0.0 and 1.0
    n_iter:int
        Passes over the training dataset.

    Attributes
    ----------
    w_:1d-array
        weights after fitting.
    errors_:list
        Number of miscalssifications in every epoch.

    """

    def __init__(self, eta=0.01, n_iter=10):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self, X, y):
        """Fit training data.

        :param X:{array-like}, shape=[n_samples, n_features]
        Training vectors,
        :param y: array-like, shape=[n_samples]
        Target values.
        :return:
        self:object

        """

        self.w_ = np.zeros(1 + X.shape[1]) # Add w_0
        self.cost_ = []

        for i in range(self.n_iter):
            output = self.net_input(X)
            errors = (y - output)
            self.w_[1:] += self.eta * X.T.dot(errors)
            self.w_[0] += self.eta * errors.sum()
            cost = (errors ** 2).sum() / 2.0
            self.cost_.append(cost)
        return self

    def net_input(self, X):
        """Calculate net input"""
        return np.dot(X, self.w_[1:]) + self.w_[0]
    
    def activation(self, X):
        """Computer linear activation"""
        return self.net_input(X)
    
    def predict(self, X):
        """Return class label after unit step"""
        return np.where(self.activation(X) >= 0.0, 1, -1)
 

分別使用不同的學習率（0.01和0.0001）訓練，觀察神經元學習過程。其中學習率、迭代次數我們稱他們為超引數（hyperparameters），我們可以手動設定，超引數設定的是否合適對於整個訓練過程都很重要。

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(8,4))
ada1 = AdalineGD(n_iter=10, eta=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epochs')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline - Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, eta=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epochs')
ax[1].set_ylabel('Sum-squared-error')
ax[1].set_title('Adaline - Learning rate 0.0001')
plt.show()

可以看出，左圖中學習率為0.01，隨著迭代次數的增加，誤差在增加，說明學習率設定的不合適，產生了很大的危害，而右圖學習率為0.0001，隨著迭代次數的增加，誤差在減少，但是減少的過於緩慢，演算法收斂的很慢，訓練的效率太低，所以我們可以看出過大或過小的學習率都是不合適的。

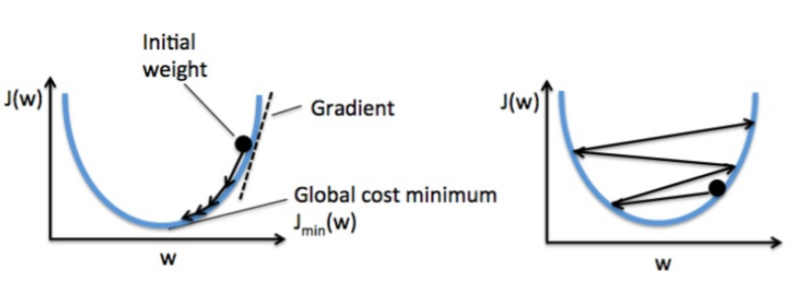
由右圖可以看出，如果學習率過大，就會導致每次梯度下降時都跳過了對應最小值的權重向量w，使得演算法無法收斂。

接下來我們介紹一種資料預處理方法，在訓練前將特徵進行某種縮放操作，這裡我們稱為特徵標準化，可以使所有特徵資料縮放成平均值為0，方差為1，加快模型的訓練速度，而且可以避免模型學習的很扭曲。

具體公式如下：
\[ x_j^, = \frac {x_j-\mu_j}{\sigma_j} \]
具體實現如下：

X_std = np.copy(X)

X_std[:, 0] = (X[:,0] - X[:,0].mean()) / X[:,0].std()

X_std[:, 1] = (X[:,1] - X[:,1].mean()) / X[:,1].std()

資料已經預處理結束，接下來我們開始訓練模型

ada = AdalineGD(n_iter=15, eta=0.01)
ada.fit(X_std, y)

plot_decision_region(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc='upper left')
plt.show()

plt.plot(range(1, len(ada.cost_) + 1), ada.cost_, marker='o')
plt.xlabel('Epoches')
plt.ylabel('Sum-squared_error')
plt.show()

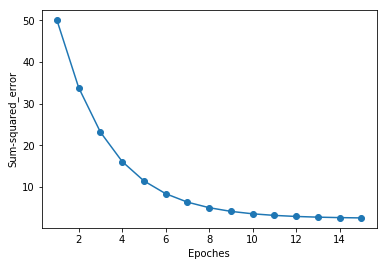
從上圖看出，隨著迭代次數的增加，誤差逐漸降低，雖然學習率為0.01，在進行標準化之前，演算法並不能收斂，但經過標準化後，演算法最終收斂