Google 的研究人員於2019年10月23號發表在Nature（《自然》《科學》及《細胞》雜誌都是國際頂級期刊，貌似在上面發文兩篇，就可以評院士了）上，關於量子計算方面（基於 Sycamore晶片）的具有里程碑式緊進展的論文，受到國內外同行及媒體的廣泛關注，包括中科大量子科學家 — 潘建偉及其團隊。特朗普的女兒Ivanka Trump（左一）也發twitter表示祝賀，如下圖：

Even as Ivanka praised the parties involved in this new quantum computing achievement, a number of social media users appeared critical of her assessment of the Trump administration's role in this endeavour.

IBM表示不服，Google不管。下面讓我們逐字逐句來看他們的論文吧，對於爭論的事務，自己下功夫下來搞清楚。

Quantum supremacy using a programmable superconducting processor

基於可程式設計的超導處理器實現的量子霸權 

 相關資源：https://doi.org/10.1038/s41586-019-1666-5

 接收日期：2019年7月20日

 核准日期：2019年9月20日

 線上釋出：2019年10月23日

Abstract

引言

量子計算機吹牛逼說，對於特定的計算任務，基於量子處理器的計算機，其速度要比經典處理器成指數級增長。根本的挑戰在於構建一個能夠在海量的計算空間上執行量子演算法的高保真處理器。我們的報告是關於，一個基於53量子位元實現的可程式設計的超導量子晶片，在2⁵³

我們用經典模擬驗證了重複實驗測量結果的取樣概率分佈。我們的Sycamore處理器取樣一個量子電路100萬次，大約花了200秒——我們的基準測試表明，同樣的任務最先進的超級計算機大約需要花費10000年。相較於所有已知的經典演算法，對於這個特定的計算任務，用實驗實現的量子優越性在速度方面的顯著提升，預示著一個期待已久的計算正規化。

Main

正文

早在20世紀80年代，有鑑於經典計算機在模擬大型量子系統時的高昂成本，理查德·費曼（Richard Feynman）就提出量子計算機將是解決物理、化學問題的有效工具。將費曼的設想付諸現實，構成了重大的實驗和理論挑戰。

首先，一個能夠在足夠巨大的計算空間（hibert）進行計算並且以低錯誤率提供量子加速的量子系統，工程上是否可行？其次，我們能否構建一個對於經典計算機很難但是對於量子計算機比較簡單的問題？通過在我們的超導量子處理器上運算這樣的一個基準任務，我們解決了這2個問題。我們的實驗實現了量子優越性，這是全面實現量子計算征程的里程碑。

在實現里程碑的過程中，我們證明了量子加速在現實世界是可達到的，也沒有被任何未知的物理定律所排除。量子優越性也預示著嘈雜的中型量子（NISQ，筆者：嘈雜意味著不穩定，噪音嚴重）技術時代的到來。我們論證的基準任務，已經立即用於生成可認證的隨機數（S. Aaronson，手稿正則準備中）；這個新的計算能力的最初應用領域可能包括優化機器學習、材料科學和化學。然而，實現完全意義的量子計算（例如，Shor的分解演算法）仍然有待於技術的飛越以製造支援容錯邏輯的量子位元。

為了達成量子優越性，我們取得了一系列的技術進步，從而為糾錯鋪平了道路。我們研製了可以同時執行跨兩個維度量子矩陣的快速高保真門。我們使用了強大的新工具：交叉熵基準，在元件和系統層面對處理器進行了校準和基準測試。最後，為了精確預測整個系統的效能，我們使用了元件級的保真度，從而進一步證明當擴充套件到大型系統時量子資訊的行為符合預期。

A suitable computational task

合適的計算任務

為了證明量子優越性，我們在取樣量子電路的偽隨機輸出任務中，比較我們的量子處理器和最新的經典計算機。隨機電路是基準測試的一個合適選擇，因為它門不具有結構，因此可以有限地保證計算硬度。我們設計的電路通過重複應用單量子和雙量子邏輯運算實現了一組量子的糾纏。取樣量子電路的輸出生成了一串位元串，例如｛0000101, 1011100, …｝。由於量子干擾的存在，位元串的概率分佈類似於在鐳射散射中的光干擾產生的強模型的斑點，因此有些位元串比其它的更容易出現。隨著量子位元的數量（寬度）和門迴圈數量（深度）的增加，概率分佈之經典計算的難度呈指數級增加。

我們使用稱為交叉熵基準測試的方法來驗證量子處理器是否正常工作，該方法將通過比較實驗觀察的每個位元串的頻率與通過經典計算機的模擬計算得出對應的理想概率。對於給定的電路，我們收集測得的位元串{xi}並且計算線性交叉熵基準的保真度（另請參見補充資訊），這是我們測得的位元串的模擬概率的平均值：

F_XEBY= 2ⁿ<P(x_i)>_i  ‐ 1

其中n是量子位元的總數，P(x_i) 是為理想的量子電路計算的位串 xi 的概率，並且平均值超過了觀察到的位元串。直觀地講，F_XEB和我們取樣高概率的位元串的頻率相關。當量子電路沒有錯誤的時候，其概率分佈呈指數分佈 （請參見補充資訊），從這個分佈取樣將使得F_XEB = 1。另一方面，從均勻分佈取樣將得到：⟨P(xi)⟩i = 1/2ⁿ ,F_XEB  = 1。F_XEB的值介於0和1之間，表示電路執行時沒有錯誤發生的概率。概率（P(x_i) ）必須從經典模擬量子電路得到，因此在至高無上的量子優越性上面計算F_XEB十分棘手。然而，通過某些簡化的電路，我們可以估計出在寬和深量子電路上滿載執行的處理器的定量保真度。

 我們的目標是通過足夠寬和深的電路實現足夠高的F_XEB，這樣經典計算的成本將高的難以承受。這是一個艱鉅的任務，因為我們的邏輯閘並不完美，我們打算構造的量子態對錯誤也很敏感。在演算法執行過程中，單個位元或相位的翻轉將徹底重構斑點圖案並且導致保真度逼近0（請參見補充資訊）。因此，為了宣稱量子的優越性，我們需要一個能夠以非常低的錯誤率執行程式的量子處理器。

Building a high-fidelity processor

構建高保真處理器

我們設計了一個名為“Sycamore”的量子處理器，它由54個特蘭蒙量子位元的二維陣列組成，其中每個量子位可調耦合到一個矩形格子的四個最近的相鄰接點。選擇這個連線是為了與使用表層程式碼之糾錯向前相容。這個裝置的一項關鍵性系統進步是它實現了單量子位元和雙量子位元運算的高保真度，不單單是孤立的，而且可以在許多量子位元上同時進行門運算和現實計算。我們接下來討論重點，也請參見補充資訊。

在一個超導量子比特里，傳導電子會凝聚成巨集觀量子態，這樣電流和電壓會機械地呈現出量子態。我們的處理器使用特蘭蒙量子位元，可以將其視為擁有5-7 G赫茲主頻的非線性超導諧振器。其量子位元被編碼為諧振電路的兩個最低量子本徵態。每個特蘭蒙都有兩個控制器：一個微波驅動器來激發量子位元，以及一個磁通量控制器來調製頻率。每個量子位元被連線到用於讀出量子位元狀態的線性諧振器。如圖1所示，每個量子位元同時通過一個新的可調耦合器連線到其相鄰的量子位元。我們的耦合器設計允許我們快速將量子位元—量子位元耦合從完全關停調整到40 M赫茲。1個量子位元無法正常運轉，所以這個裝置用了53個量子位元和86個耦合器。

 　　　　　　　　　　圖.1 : Sycamore 處理器

為了金屬化和約瑟夫森連線，處理器用鋁製造，並使用銦製造兩個矽晶片之間的凸點。晶片用引線粘合到超導電路板上，並在稀釋冰箱中冷卻至20 mK以下，以將環境熱能降低到大大低於量子位元能。處理器通過濾波器和衰減器連線到處於室溫的電子裝置，該裝置可合成控制訊號。使用頻率複用技術可以同時讀取所有量子位元的狀態。我們用兩級低溫放大器來增強訊號，該訊號被數字化（在1 G赫茲頻率時為8位元）並在室溫下通過數字化實現解複用。為了完全控制量子處理器，我們總共設計了277個數模轉換器（在1G赫茲頻率時為14位元）

 我們通過驅動25納秒的微波脈衝來執行單量子位元門，該微波脈衝會以量子頻率共振，同時關閉量子位元-量子位元耦合。脈衝經過整形，從而最大程度地避免了過渡到更高的特蘭蒙狀態。由於兩級系統缺陷，門的效能會隨頻率產生很大的變化，雜散微波模式會與控制線和讀出諧振器相耦合，量殘餘的雜散耦合於量子位元、磁通噪聲和脈衝失真。有鑑於此，我們優化了單量子位元操作頻率以減免這些錯誤機制。

我們使用上述交叉熵基準測試協議對單量子位元門的效能進行基準測試，降低到單量子位元級別（n = 1），以測量在單量子位元門期間發生錯誤的概率。在每個量子位元上，我們應用數量可變的m個隨機選擇的門，並在許多序列上測量F_XEB的平均值；隨著m的增加，誤差會累積、F_XEB的平均值會下降。我們用[1 − e₁ /（1 − 1 / D²）] ^m對該衰減建模，其中e₁是Pauli誤差概率。在這種情況下，狀態（希爾伯特）的空間量綱，D = 2ⁿ，等於2，它校正了誤差與理想態部分重疊的去極化模型。該過程類似於更典型的隨機基準測試，但支援非Clifford門的集合，並且可以將消退相干誤差與相干控制誤差區分開。然後，我們重複了所有量子位元同時執行單量子位元門的實驗（圖2），而錯誤率僅僅表現出微小的增長，表明我們裝置的微波干擾率很低。

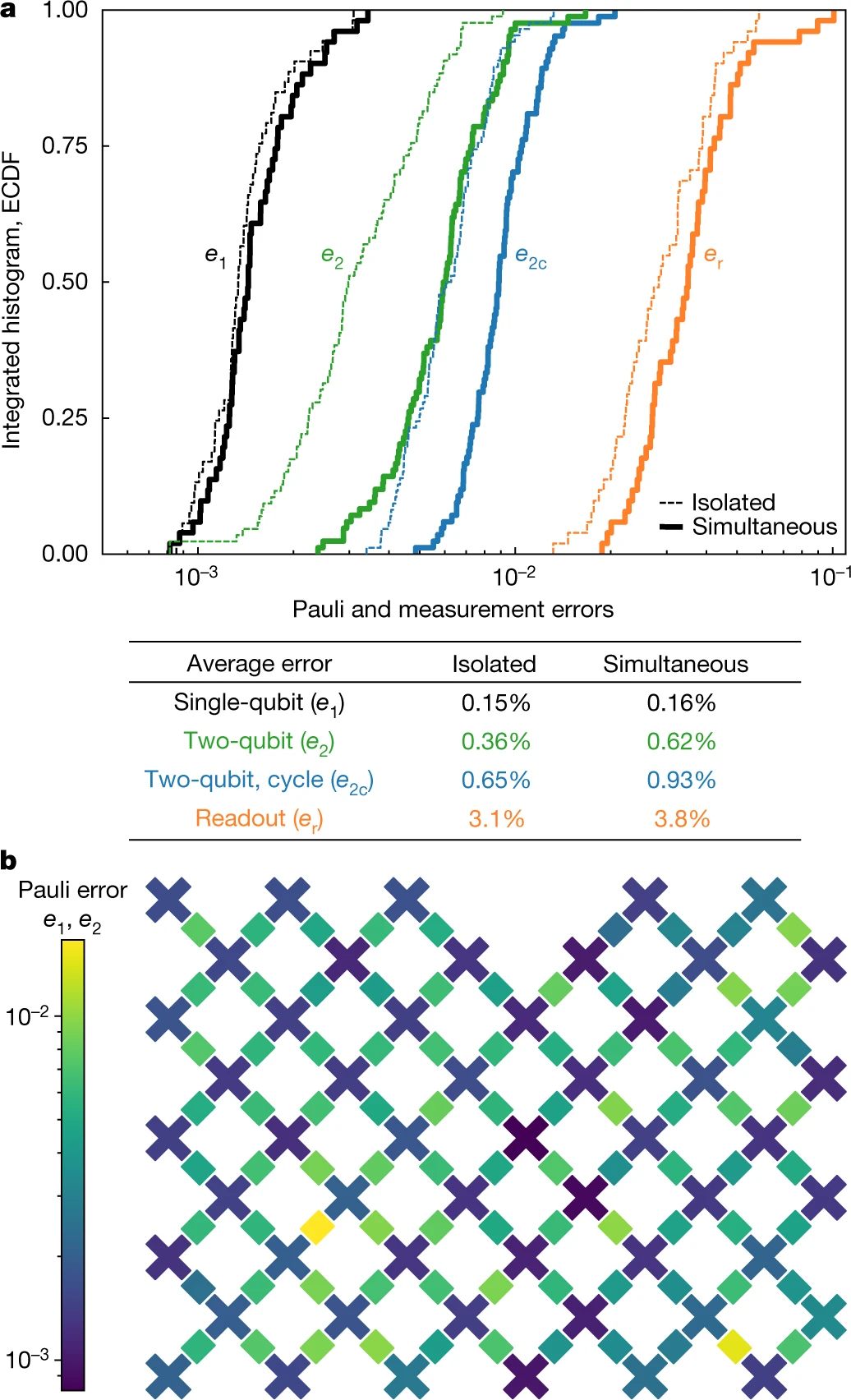
 　　　　　　　　圖.2 : 全系統的 Pauli 和 測量錯誤

我們通過持續開啟20 M赫茲耦合12 納秒,並使相鄰的量子位共振來執行類似iSWAP的兩個量子位元糾纏門，從而允許量子位元可以交換激勵。在此期間，量子位元還經歷了受控相位（CZ）的互動作用，該互動作用來自於更高級別的特蘭蒙。優化每對量子位元的兩個量子位元門限頻率軌跡，是為了減少在優化單量子位元工作頻率時所要考慮的相同錯誤機制。

為了表徵和量化兩個量子位元門，我們運行了m個週期的兩個量子位元電路，每個週期在每個雙量子位元上都包含一個隨機選擇的單量子位元門，緊跟著固定的兩個量子位元門。通過使用F_XEB作為成本函式，我們學習了兩個量子單位的引數（例如iSWAP和CZ互動的數量）。經過這次優化，我們從值為 m 的F_XEB的衰變中提取每週期錯誤e_2c，並減去兩個單量子位元的錯誤e₁來分離出兩個量子位元錯誤e₂。我們發現e₂的平均值為0.36％。 另外，我們在為整個矩陣同步執行雙量子位元電路的同時重複執行相同的過程。在為諸如，色散漂移和串擾等，考慮影響而更新單一引數後，我們發現e₂的平均值為0.62％。

對於整個實驗，我們在同步操作期間用兩個量子位元元測量每一對，而不是所有對的標準門，生成量子電路。典型的兩個量子位元門是一個全iSWAP，並且擁有1/6的全CZ。絕不使用單獨校準的門來限制演示的通用性。例如，1個量子位元門和任意給定對中的兩個唯一的量子位元門可以組成可控NOT（CNOT）門。高保真“教科書似的門”，例如CZ或√iSWAP ，的製作正在緊鑼密鼓地進行。

找到了單個門的錯誤率和讀數後，我們可以將量子電路的保真度建模為所有門和測量的0錯誤操作概率的乘積。我們最大的隨機量子電路有53個量子位元，1113個單量子位元門，430個雙量子位元門，每個量子位元一個亮度，我們估計其總保真度為0.2%。由於F_XEB的不確定度為1 /N_s-√1/ N_s（其中Ns是樣本數），因此這個保真度應該可以通過數百萬次的測量來分辨。我們的模型推測，糾纏越來越大的系統不會引入超出我們在單位元和兩位元級別上測量的誤差之外的其他錯誤源。 在下一節中，我們將瞭解該假設的成立情況。

Fidelity estimation in the supremacy regime

優越性的逼真度估算

 我們的偽隨機量子電路生成器的門序列如 圖3 所示。此演算法的一個週期由應用於所有量子的單量子（從｛√X, √Y, √Z｝隨機選擇），緊跟著的成對的量子位元上的兩個量子位元門組成。組成“優越性電路”的門序列旨在最小化為創造一個高糾纏態的電路深度，而這正是計算複雜度和經典硬度所需。

 　　　　　　　　　　　　　　　　　　圖.3 : 量子優越性電路的控制操作

儘管我們無法在至高無上的體系中計算F_XEB，但是我們可以通過降低電路的複雜度的三個變體來評估它。在“貼片電路”中，我們移除掉了兩個量子位元門的一部分（佔兩個量子位元門總數的一小部分），將電路分分割成兩個空間上隔離的，沒有相互作用的量子位元補丁。然後我們用可以輕鬆計算出保真度的補丁的乘積作為總的保真度。在“消除電路”中，我們沿切片僅去除了最初的兩個量子位元門的一小部分，允許補丁之間的糾纏，這在維持了模擬可行性的同時更緊密地模擬了整個實驗。最終，我們也可以運行同我們的優越性電路有著相同的門數的全“驗證電路”，但卻與在傳統上容易模擬的多的兩電子門序列有著不同的模式（也請參見補充資訊）。比較這些三個變體讓我們能夠在接近優越性制度的過程中追蹤系統保真度。

我們首先檢查補丁版本和刪節版本的驗證電路是否能與多達53量子位元的完整驗證電路產生相同的保真度，如圖4所示。每個資料點，我們通常在10個電路例項中採集 N_s = 5 × 10⁶的總樣本，每個例項的區別僅在於在每個週期中單個量子門的選擇不同。我們也顯示F_{XEB的預測值，}該值是通過將單量子和雙量子位元門的0錯誤率和測量值相乘而得到的（也請參見補充資訊）_。儘管在計算複雜度和糾纏存在巨大差異，這個預測值、補丁及消除的保真度都對應的全電路的保真度吻合的很好。這讓我們對消隱電路可以用於準確估計更為複雜電路的保真度充滿信心。

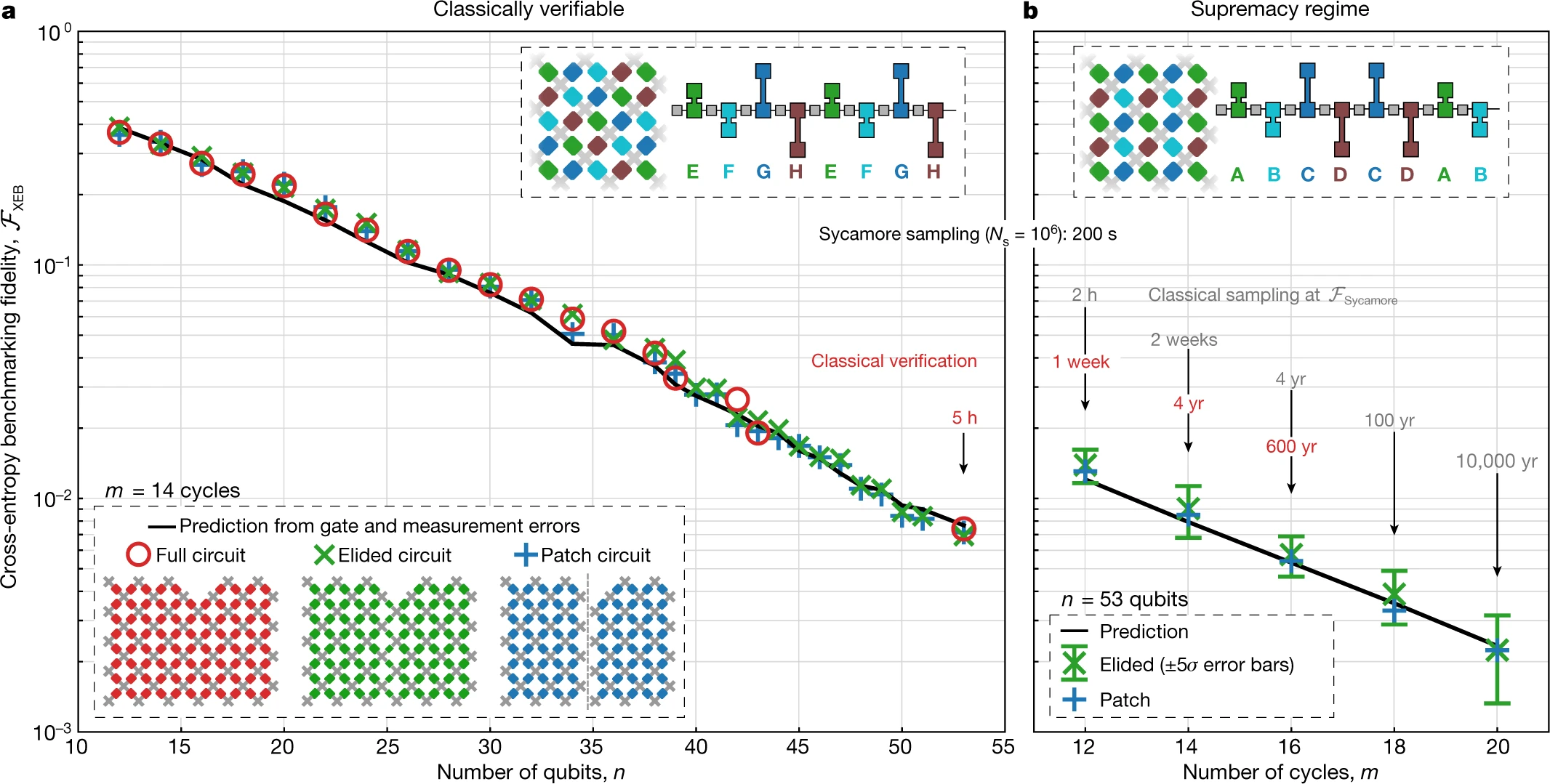
　　　　　　　　　　　　　　　　圖.4 : 量子優越性的證明

保真度仍可以直接被驗證的最大電路有53個量子位元和一個簡化處理過的閘電路。100萬個核心以0.8%的保真度對這些隨機電路進行取樣需要花費130秒，相較於單核，量子處理器有百萬倍的加速。

我們現在繼續對計算最複雜電路進行基準測試，這個只是2個位元門的重排列。在圖4中，我們顯示了通過不斷增加深度，針對53量子位元的全優越性電路的補丁版和消隱版本測得的F_XEB。對於有53個量子位元和20個週期的最大電路，我們在10個電路例項上搜集了 N_s = 30 × 10⁶

樣本，對於消隱電路得到的F_XEB = (2.24±0.21)×10⁻³。基於5σ的置信度，我們斷定在量子處理器上執行這些電路的平均保真度至少大於0.1％。我們預期 圖4b的全部資料應具有近似的保真度，但是由於模擬時間（紅色數字）需要很長時間才能檢查，我們將資料歸檔（參見“資料可用性”部分）。這部分資料因此處於量子至上的狀態。

The classical computational cost

經典計算的成本

我們在經典計算機的實驗中模擬量子電路有2個目的：（1））通過使用可能簡化的電路計算F_XEB來驗證我們的量子處理器和基準測試方法（圖4a），(2)估算F_XEB以及對最困難的電路進行取樣的經典成本（圖4b）。多達43個量子位元，我們使用Schrödinger演算法，該演算法模擬了完整量子態的演化；Jülich超級計算機（100,000核、250 TB）運行了最大的樣例。超過此大小，則沒有足夠的隨機存取儲存器（RAM）來儲存量子的狀態了。對於更多的量子位元，我們使用執行在Google資料中心的混合Schrödinger-Feynman演算法來計算單個位元串的幅度。在使用類似費曼路徑積分的方法連線它們之前，該演算法將電路拆分為兩個量子位元補丁，並使用Schrödinger方法有效地模擬每個補丁。儘管具有更高的記憶體效率，但隨著路徑深度與連線補丁的門的數量呈指數增長，隨著電路深度的增加，Schrödinger-Feynman演算法的計算量也呈指數增長。

為了估算優越性電路的經典計算成本(圖4中的灰色數字），我們在Summit超級計算機以及Google叢集上都運行了部分量子電路的模擬，從而推斷出其全部成本。在此推斷中，我們通過擴充套件F_XEB的驗證成本來認定取樣的計算成本，例如，一個0.1%減少了約1000的花費。在當今世界上功能最強大的Summit超級計算機上，我們使用了一個受費曼路徑積分啟發的方法，該方法在低深度下效率最高。當m = 20時，張量無法合理地放入節點記憶體中，因此我們只能在m=14時測量執行時間，因此我們估計以1％的保真度取樣300萬個位元串將需要一年。

在谷歌雲伺服器上，我們預估使用Schrödinger-Feynman演算法以0.1％的保真度在m = 20時執行相同的任務將耗費50萬億個核/小時，並消耗1皮瓦時的能量。從這個角度考慮，從角度來看，對量子處理器上的電路取樣三百萬次需要600秒，而取樣時間受控制硬體的通訊的限制；實際上，量子處理器的實際上，淨量子處理器的淨時間僅為30秒左右。所有電路的位元串樣本都已線上存檔（請參見“資料可用性”部分），以激勵開發和測試更高階的驗證演算法。

有人可能會懷疑演算法創新可以在多大程度上增強經典模擬效果。我們的假設基於複雜理論的認知，即演算法任務的成本是電路大小的指數。的確，在過去的幾年中，模擬演算法已經得到了穩步的提升。我們預計最終將實現比報告裡提到的更低的模擬成本，但是我們也期望更大型的量子處理器在硬體方面的改進將持續超越它們。

Verifying digital error model

驗證數字錯誤模型

基於量子錯誤校正理論的一個關鍵假設是—量子態錯誤可考慮數字化和本地化。基於這樣的一個數字模型，演化量子態中的所有錯誤都可能通過散佈在電路中的一組區域性保利誤差（位翻轉或相位翻轉）來表徵。由於持續振幅是量子力學的基礎，所以需要測試量子系統中的錯誤是否可以被視為離散的和概率的。我們實驗的觀察結果證明該模型對我們處理器確實是有效的。我們系統的保真度可以通過一個簡單的模型很好地預測，在該模型中，每個門各自的特徵保真度相乘起來（圖4）。

為了能成功被數字化誤差模型描述，系統的相關誤差得很小才行。我們通過選擇隨機化和解相關誤差的電路，優化控制以最大程度地減少系統誤差和洩漏以及設計比相關噪聲源（如1 / f磁通噪聲）執行得更快的門，從而在我們的實驗中達成了這一點。通過在高達2⁵³號希爾伯特空間對預測性不相關的誤差模型的演示，可以表明我們可以構建一個系統，在該系統中量子資源（例如糾纏）不會過於脆弱。

The future

未來

基於超導量子位元的量子處理器現在可以處理，量綱為2⁵³ ≈ 9 ×10¹⁵的希爾伯特（Hilbert）空間的計算，超出了當今最快的經典超級計算機的上限。據我們所知，此次試驗標記了只能在量子處理器執行的第一個計算。量子處理器因此達成了量子優越性的制度。我們希望他們的計算能力將繼續以雙倍指數的比率增長：模擬量子電路的經典成本隨著計算量的增加而呈指數級的增長，而硬體的提升將可能遵循量子處理器當量的摩爾定律，即每隔幾年此計算量就翻倍。為了支撐雙指數級的增長率並最終提供運算著名的，如Shor 或者Grover ，量子演算法所需的計算量，量子誤差修正的工程學將成為關注的焦點。

Bernstein 和 Vazirani 闡述的擴充套件自Church–Turing的論文，斷言任何合理的模型都可以由圖靈機器有效的模擬。

Data availability

資料可用性

用於本次研究形成和分析的資料庫可在我麼公開的樹妖（Dryad）倉庫上獲得 (https://doi.org/10.5061/dryad.k6t1rj8)。

線上內容

 任何方法、額外參考、自然研究的報告摘要、源資料、擴充套件資料、補充資訊、確認書、同行評審資訊；作者貢獻和利益衝突的詳細資訊； 以及資料和程式碼可用性均可在 https://doi.org/10.1038/s41586-019-1666-5 得到。

初次嘗試翻譯，錯誤之處必不在少，歡迎批評指正

附：

1）英文論文下載： Quantum supremacy using a programmable superconducting processor 

2）「量子霸權」真的來了：谷歌論文正式在《自然》雜誌發表；藉助 54 個量子位元的 Sycamore 晶片實現（附論文）

*****************************************************************************************************

精力有限，想法太多，專注做好一件事就行

• 我只是一個程式猿。5年內把程式碼寫好，技術部落格字字推敲，堅持零拷貝和原創
• 寫部落格的意義在於鍛鍊邏輯條理性，加深對知識的系統性理解，鍛鍊文筆，如果恰好又對別人有點幫助，那真是一件令人開心的事

*****************************************************************************************************

&n