利用Python學習線性代數 -- 1.1 線性方程組
利用Python學習線性代數 -- 1.1 線性方程組
利用Python學習線性代數系列,第一節
本節實現的主要功能函式,在原始碼檔案linear_system中,後續章節將作為基本功能呼叫。
線性方程
線性方程組由一個或多個線性方程組成,如
\[
\begin{array}\\
x_1 - 2 x_2 &= -1\\
-x_1 + 3 x_2 &= 3
\end{array}
\]
求包含兩個變數兩個線性方程的方程組的解,等價於求兩條直線的交點。
這裡可以畫出書圖1-1和1-2的線性方程組的圖形。
通過改變線性方程的引數,觀察圖形,體會兩個方程對應直線平行、相交、重合三種可能。
那麼,怎麼畫二元線性方程的直線呢?
方法是這樣的:
假如方程是 \(a x_1 + b x_2 = c\) 的形式,可以寫成 \(x_2 = (c - a x_1) / b\)。
在以 \(x_1\) 和\(x_2\)為兩個軸的直角座標系中,\(x_1\)取一組值,如 \((-3, -2.9, -2.8, \dots, 2.9, 3.0)\),
計算相應的 \(x_2\),然後把所有點 \((x_1, x_2)\) 連起來成為一條線。
當 \(b\) 為 \(0\) 時, 則在\(x_1 = c / a\)處畫一條垂直線。
# 引入Numpy和 Matplotlib庫 import numpy as np from matplotlib import pyplot as plt
Matplotlib 是Python中使用較多的視覺化庫,這裡只用到了它的一些基本功能。
def draw_line(a, b, c, start=-4, stop=5, step=0.01): """根據線性方程引數繪製一條直線""" # 如果b為0,則畫一條垂線 if np.isclose(b, 0): plt.vlines(start, stop, c / a) else: # 否則畫 y = (c - a*x) / b xs = np.arange(start, stop, step) plt.plot(xs, (c - a*xs)/b)
# 1.1 圖1-1
draw_line(1, -2, -1)
draw_line(-1, 3, 3)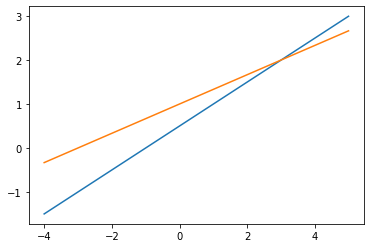
def draw_lines(augmented, start=-4,
stop=5, step=0.01):
"""給定增廣矩陣,畫兩條線."""
plt.figure()
for equation in augmented:
draw_line(*equation, start, stop, step)
plt.show()# Fig. 1-1
# 增廣矩陣用二維陣列表示
# [[1, -2, -1], [-1, 3, 3]]
# 這些數字對應圖1-1對應方程的各項係數
draw_lines([[1, -2, -1], [-1, 3, 3]])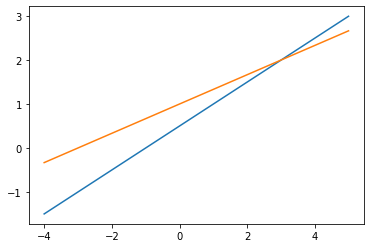
# Fig. 1-2
draw_lines([[1, -2, -2], [-1, 2, 3]])
# Fig. 1-3
draw_lines([[1, -2, -1], [-1, 2, 1]])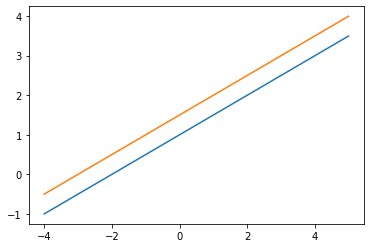
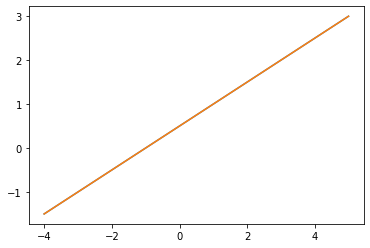
- 建議:改變這些係數,觀察直線,體會兩條直線相交、平行和重合的情況
例如
draw_lines([[1, -2, -2], [-1, 2, 9]])如果對Numpy比較熟悉,則可以採用更簡潔的方式實現上述繪圖功能。
在計算多條直線方程時,可以利用向量程式設計的方式,用更少的程式碼實現。
def draw_lines(augmented, start=-4,
stop=5, step=0.01):
"""Draw lines represented by augmented matrix on 2-d plane."""
am = np.asarray(augmented)
xs = np.arange(start, stop, step).reshape([1, -1])
# 同時計算兩條直線的y值
ys = (am[:, [-1]] - am[:, [1]]*xs) / am[:, [0]]
for y in ys:
plt.plot(xs[0], y)
plt.show()矩陣記號
矩陣是一個數表,在程式中通常用二維陣列表示,例如
# 巢狀列表表示矩陣
matrix = [[1, -2, 1, 0],
[0, 2, -8, 8],
[5, 0, -5, 10]]
matrix[[1, -2, 1, 0], [0, 2, -8, 8], [5, 0, -5, 10]]實際工程和研究實踐中,往往會採用一些專門的數值計算庫,簡化和加速計算。
Numpy庫是Python中數值計算的常用庫。
在Numpy中,多維陣列型別稱為ndarray,可以理解為n dimensional array。
例如
# Numpy ndarray 表示矩陣
matrix = np.array([[1, -2, 1, 0],
[0, 2, -8, 8],
[5, 0, -5, 10]])
matrixarray([[ 1, -2, 1, 0],
[ 0, 2, -8, 8],
[ 5, 0, -5, 10]])解線性方程組
本節解線性方程組的方法是 高斯消元法,利用了三種基本行變換。
- 把某個方程換成它與另一個方程的倍數的和;
- 交換兩個方程的位置;
- 某個方程的所有項乘以一個非零項。
假設線性方程的增廣矩陣是\(A\),其第\(i\)行\(j\)列的元素是\(a_{ij}\)。
消元法的基本步驟是:
- 增廣矩陣中有 \(n\) 行,該方法的每一步處理一行。
- 在第\(i\)步,該方法處理第\(i\)行
- 若\(a_{ii}\)為0,則在剩餘行 \(\{j| j \in (i, n]\}\)中選擇絕對值最大的行\(a_{ij}\)
- 若\(a_{ij}\)為0,返回第1步。
- 否則利用變換2,交換\(A\)的第\(i\)和\(j\)行。
- 若\(a_{ii}\)為0,則在剩餘行 \(\{j| j \in (i, n]\}\)中選擇絕對值最大的行\(a_{ij}\)
- 利用行變換3,第\(i\)行所有元素除以\(a_{ii}\),使第 \(i\) 個方程的第 \(i\)個 係數為1
- 利用行變換1,\(i\)之後的行減去第\(i\)行的倍數,使這些行的第 \(i\) 列為0
- 在第\(i\)步,該方法處理第\(i\)行
為了理解這些步驟的實現,這裡先按書中的例1一步步計算和展示,然後再總結成完整的函式。
例1的增廣矩陣是
\[ \left[ \begin{array} &1 & -2 & 1 & 0\\ 0 & 2 & -8 & 8\\ 5 & 0 & -5 & 10 \end{array} \right] \]
# 增廣矩陣
A = np.array([[1, -2, 1, 0],
[0, 2, -8, 8],
[5, 0, -5, 10]])
# 行號從0開始,處理第0行
i = 0
# 利用變換3,將第i行的 a_ii 轉成1。這裡a_00已經是1,所不用動
# 然後利用變換1,把第1行第0列,第2行第0列都減成0。
# 這裡僅需考慮i列之後的元素,因為i列之前的元素已經是0
# 即第1行減去第0行的0倍
# 而第2行減去第0行的5倍
A[i+1:, i:] = A[i+1:, i:] - A[i+1:, [i]] * A[i, i:]
Aarray([[ 1, -2, 1, 0],
[ 0, 2, -8, 8],
[ 0, 10, -10, 10]])i = 1
# 利用變換3,將第i行的 a_ii 轉成1。
A[i] = A[i] / A[i, i]
Aarray([[ 1, -2, 1, 0],
[ 0, 1, -4, 4],
[ 0, 10, -10, 10]])# 然後利用變換1,把第2行第i列減成0。
A[i+1:, i:] = A[i+1:, i:] - A[i+1:, [i]] * A[i, i:]
Aarray([[ 1, -2, 1, 0],
[ 0, 1, -4, 4],
[ 0, 0, 30, -30]])i = 2
# 利用變換3,將第i行的 a_ii 轉成1。
A[i] = A[i] / A[i, i]
Aarray([[ 1, -2, 1, 0],
[ 0, 1, -4, 4],
[ 0, 0, 1, -1]])消元法的前向過程就結束了,我們可以總結成一個函式
def eliminate_forward(augmented):
"""
消元法的前向過程.
返回行階梯形,以及先導元素的座標(主元位置)
"""
A = np.asarray(augmented, dtype=np.float64)
# row number of the last row
pivots = []
i, j = 0, 0
while i < A.shape[0] and j < A.shape[1]:
A[i] = A[i] / A[i, j]
if (i + 1) < A.shape[0]: # 除最後一行外
A[i+1:, j:] = A[i+1:, j:] - A[i+1:, [j]] * A[i, j:]
pivots.append((i, j))
i += 1
j += 1
return A, pivots這裡有兩個細節值得注意
- 先導元素 \(a_{ij}\),不一定是在主對角線位置,即 \(i\) 不一定等於\(j\).
- 最後一行只需要用變換3把先導元素轉為1,沒有剩餘行需要轉換
# 測試一個增廣矩陣,例1
A = np.array([[1, -2, 1, 0],
[0, 2, -8, 8],
[5, 0, -5, 10]])
A, pivots = eliminate_forward(A)
print(A)
print(pivots)[[ 1. -2. 1. 0.]
[ 0. 1. -4. 4.]
[ 0. 0. 1. -1.]]
[(0, 0), (1, 1), (2, 2)]消元法的後向過程則更簡單一些,對於每一個主元(這裡就是前面的\(a_{ii}\)),將其所在的列都用變換1,使其它行對應的列為0.
for i, j in reversed(pivots):
A[:i, j:] = A[:i, j:] - A[[i], j:] * A[:i, [j]]
Aarray([[ 1., 0., 0., 1.],
[ 0., 1., 0., 0.],
[ 0., 0., 1., -1.]])def eliminate_backward(simplified, pivots):
"""消元法的後向過程."""
A = np.asarray(simplified)
for i, j in reversed(pivots):
A[:i, j:] = A[:i, j:] - A[[i], j:] * A[:i, [j]]
return A至此,結合 eliminate_forward 和eliminate_backward函式,可以解形如例1的線性方程。
然而,存在如例3的線性方程,在eliminate_forward演算法進行的某一步,主元為0,需要利用變換2交換兩行。
交換行時,可以選擇剩餘行中,選擇當前主元列不為0的任意行,與當前行交換。
這裡每次都採用剩餘行中,當前主元列絕對值最大的行。
補上行交換的前向過程函式如下
def eliminate_forward(augmented):
"""消元法的前向過程"""
A = np.asarray(augmented, dtype=np.float64)
# row number of the last row
pivots = []
i, j = 0, 0
while i < A.shape[0] and j < A.shape[1]:
# if pivot is zero, exchange rows
if np.isclose(A[i, j], 0):
if (i + 1) < A.shape[0]:
max_k = i + 1 + np.argmax(np.abs(A[i+1:, i]))
if (i + 1) >= A.shape[0] or np.isclose(A[max_k, i], 0):
j += 1
continue
A[[i, max_k]] = A[[max_k, i]]
A[i] = A[i] / A[i, j]
if (i + 1) < A.shape[0]:
A[i+1:, j:] = A[i+1:, j:] - A[i+1:, [j]] * A[i, j:]
pivots.append((i, j))
i += 1
j += 1
return A, pivots行交換時,有一種特殊情況,即剩餘所有行的主元列都沒有非零元素。
這種情況下,在當前列的右側尋找不為零的列,作為新的主元列。
# 用例3測試eliminate_forward
aug = [[0, 1, -4, 8],
[2, -3, 2, 1],
[4, -8, 12, 1]]
echelon, pivots = eliminate_forward(aug)
print(echelon)
print(pivots)[[ 1. -2. 3. 0.25]
[ 0. 1. -4. 0.5 ]
[ 0. 0. 0. 1. ]]
[(0, 0), (1, 1), (2, 3)]例3化簡的結果與書上略有不同,由行交換策略不同引起,也說明同一個矩陣可能由多個階梯形。
結合上述的前向和後向過程,即可以給出一個完整的消元法實現
def eliminate(augmented):
"""
利用消元法前向和後向步驟,化簡線性方程組.
如果是矛盾方程組,則僅輸出前向化簡結果,並列印提示
否則輸出簡化後的方程組,並輸出最後一列
"""
print(np.asarray(augmented))
A, pivots = eliminate_forward(augmented)
print(" The echelon form is\n", A)
print(" The pivots are: ", pivots)
pivot_cols = {p[1] for p in pivots}
simplified = eliminate_backward(A, pivots)
if (A.shape[1]-1) in pivot_cols:
print(" There is controdictory.\n", simplified)
elif len(pivots) == (A.shape[1] -1):
print(" Solution: ", simplified[:, -1])
is_correct = solution_check(np.asarray(augmented),
simplified[:, -1])
print(" Is the solution correct? ", is_correct)
else:
print(" There are free variables.\n", simplified)
print("-"*30)eliminate(aug)[[ 0 1 -4 8]
[ 2 -3 2 1]
[ 4 -8 12 1]]
The echelon form is
[[ 1. -2. 3. 0.25]
[ 0. 1. -4. 0.5 ]
[ 0. 0. 0. 1. ]]
The pivots are: [(0, 0), (1, 1), (2, 3)]
There is controdictory.
[[ 1. 0. -5. 0.]
[ 0. 1. -4. 0.]
[ 0. 0. 0. 1.]]
------------------------------利用 Sympy 驗證消元法實現的正確性
Python的符號計算庫Sympy,有化簡矩陣為行最簡型的方法,可以用來檢驗本節實現的程式碼是否正確。
# 匯入 sympy的 Matrix模組
from sympy import MatrixMatrix(aug).rref(simplify=True)
# 返回的是行最簡型和主元列的位置(Matrix([
[1, 0, -5, 0],
[0, 1, -4, 0],
[0, 0, 0, 1]]), (0, 1, 3))echelon, pivots = eliminate_forward(aug)
simplified = eliminate_backward(echelon, pivots)
print(simplified, pivots)
# 輸出與上述rref一致[[ 1. 0. -5. 0.]
[ 0. 1. -4. 0.]
[ 0. 0. 0. 1.]] [(0, 0), (1, 1), (2, 3)]綜合前向和後向步驟,並結果的正確性
綜合前向和後向消元,就可以得到完整的消元法過程。
消元結束,如果沒有矛盾(最後一列不是主元列),基本變數數與未知數個數一致,則有唯一解,可以驗證解是否正確。
驗證的方法是將解與係數矩陣相乘,檢查與原方程的b列一致。
def solution_check(augmented, solution):
# 係數矩陣與解相乘
b = augmented[:, :-1] @ solution.reshape([-1, 1])
b = b.reshape([-1])
# 檢查乘積向量與b列一致
return all(np.isclose(b - augmented[:, -1], np.zeros(len(b))))def eliminate(augmented):
from sympy import Matrix
print(np.asarray(augmented))
A, pivots = eliminate_forward(augmented)
print(" The echelon form is\n", A)
print(" The pivots are: ", pivots)
pivot_cols = {p[1] for p in pivots}
simplified = eliminate_backward(A, pivots)
if (A.shape[1]-1) in pivot_cols: # 最後一列是主元列
print(" There is controdictory.\n", simplified)
elif len(pivots) == (A.shape[1] -1): # 唯一解
is_correct = solution_check(np.asarray(augmented),
simplified[:, -1])
print(" Is the solution correct? ", is_correct)
print(" Solution: \n", simplified)
else: # 有自由變數
print(" There are free variables.\n", simplified)
print("-"*30)
print("對比Sympy的rref結果")
print(Matrix(augmented).rref(simplify=True))
print("-"*30)測試書中的例子
aug_1_1_1 = [[1, -2, 1, 0],
[0, 2, -8, 8],
[5, 0, -5, 10]]
eliminate(aug_1_1_1)
# 1.1 example 3
aug_1_1_3 = [[0, 1, -4, 8],
[2, -3, 2, 1],
[4, -8, 12, 1]]
eliminate(aug_1_1_3)
eliminate([[1, -6, 4, 0, -1],
[0, 2, -7, 0, 4],
[0, 0, 1, 2, -3],
[0, 0, 3, 1, 6]])
eliminate([[0, -3, -6, 4, 9],
[-1, -2, -1, 3, 1],
[-2, -3, 0, 3, -1],
[1, 4, 5, -9, -7]])
eliminate([[0, 3, -6, 6, 4, -5],
[3, -7, 8, -5, 8, 9],
[3, -9, 12, -9, 6, 15]])[[ 1 -2 1 0]
[ 0 2 -8 8]
[ 5 0 -5 10]]
The echelon form is
[[ 1. -2. 1. 0.]
[ 0. 1. -4. 4.]
[ 0. 0. 1. -1.]]
The pivots are: [(0, 0), (1, 1), (2, 2)]
Is the solution correct? True
Solution:
[[ 1. 0. 0. 1.]
[ 0. 1. 0. 0.]
[ 0. 0. 1. -1.]]
------------------------------
對比Sympy的rref結果
(Matrix([
[1, 0, 0, 1],
[0, 1, 0, 0],
[0, 0, 1, -1]]), (0, 1, 2))
------------------------------
[[ 0 1 -4 8]
[ 2 -3 2 1]
[ 4 -8 12 1]]
The echelon form is
[[ 1. -2. 3. 0.25]
[ 0. 1. -4. 0.5 ]
[ 0. 0. 0. 1. ]]
The pivots are: [(0, 0), (1, 1), (2, 3)]
There is controdictory.
[[ 1. 0. -5. 0.]
[ 0. 1. -4. 0.]
[ 0. 0. 0. 1.]]
------------------------------
對比Sympy的rref結果
(Matrix([
[1, 0, -5, 0],
[0, 1, -4, 0],
[0, 0, 0, 1]]), (0, 1, 3))
------------------------------
[[ 1 -6 4 0 -1]
[ 0 2 -7 0 4]
[ 0 0 1 2 -3]
[ 0 0 3 1 6]]
The echelon form is
[[ 1. -6. 4. 0. -1. ]
[ 0. 1. -3.5 0. 2. ]
[ 0. 0. 1. 2. -3. ]
[-0. -0. -0. 1. -3. ]]
The pivots are: [(0, 0), (1, 1), (2, 2), (3, 3)]
Is the solution correct? True
Solution:
[[ 1. 0. 0. 0. 62. ]
[ 0. 1. 0. 0. 12.5]
[ 0. 0. 1. 0. 3. ]
[-0. -0. -0. 1. -3. ]]
------------------------------
對比Sympy的rref結果
(Matrix([
[1, 0, 0, 0, 62],
[0, 1, 0, 0, 25/2],
[0, 0, 1, 0, 3],
[0, 0, 0, 1, -3]]), (0, 1, 2, 3))
------------------------------
[[ 0 -3 -6 4 9]
[-1 -2 -1 3 1]
[-2 -3 0 3 -1]
[ 1 4 5 -9 -7]]
The echelon form is
[[ 1. 1.5 -0. -1.5 0.5]
[-0. 1. 2. -3. -3. ]
[-0. -0. -0. 1. -0. ]
[ 0. 0. 0. 0. 0. ]]
The pivots are: [(0, 0), (1, 1), (2, 3)]
There are free variables.
[[ 1. 0. -3. 0. 5.]
[-0. 1. 2. 0. -3.]
[-0. -0. -0. 1. -0.]
[ 0. 0. 0. 0. 0.]]
------------------------------
對比Sympy的rref結果
(Matrix([
[1, 0, -3, 0, 5],
[0, 1, 2, 0, -3],
[0, 0, 0, 1, 0],
[0, 0, 0, 0, 0]]), (0, 1, 3))
------------------------------
[[ 0 3 -6 6 4 -5]
[ 3 -7 8 -5 8 9]
[ 3 -9 12 -9 6 15]]
The echelon form is
[[ 1. -2.33333333 2.66666667 -1.66666667 2.66666667 3. ]
[ 0. 1. -2. 2. 1.33333333 -1.66666667]
[ 0. 0. 0. 0. 1. 4. ]]
The pivots are: [(0, 0), (1, 1), (2, 4)]
There are free variables.
[[ 1. 0. -2. 3. 0. -24.]
[ 0. 1. -2. 2. 0. -7.]
[ 0. 0. 0. 0. 1. 4.]]
------------------------------
對比Sympy的rref結果
(Matrix([
[1, 0, -2, 3, 0, -24],
[0, 1, -2, 2, 0, -7],
[0, 0, 0, 0, 1, 4]]), (0, 1, 4))
------------------------------
