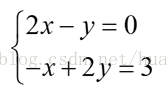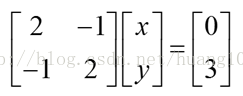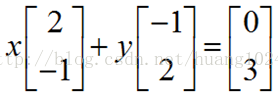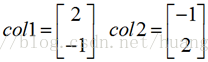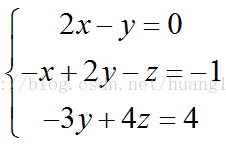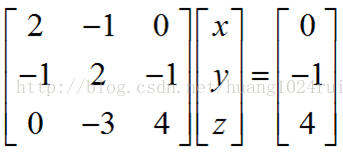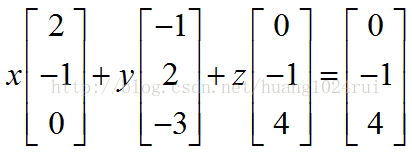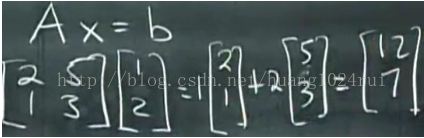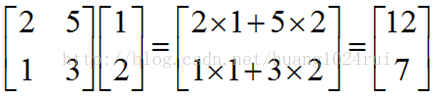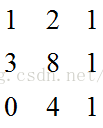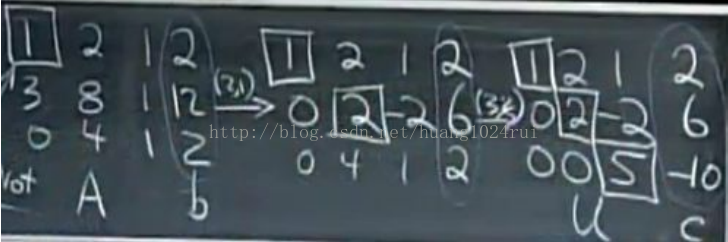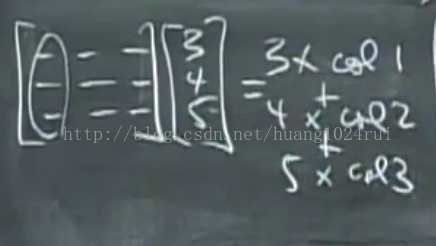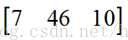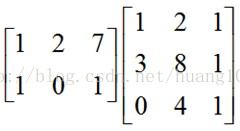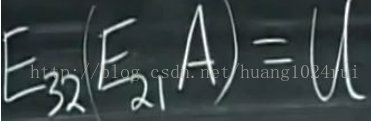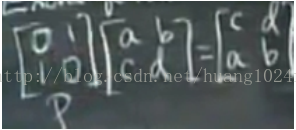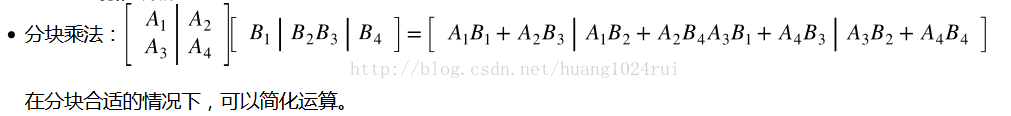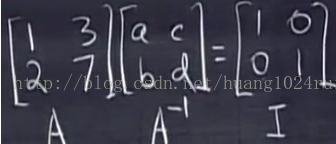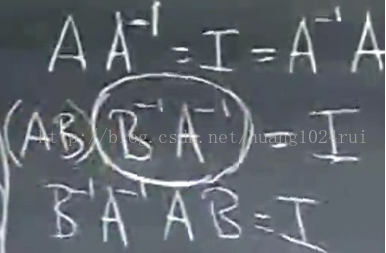MIT 線性代數(1—3)讀書筆記
幾年前把MIT Gilbert Strang教授的線性代數看完了,不過沒做筆記,很多東西都忘了,現在打算重新看一遍,邊寫邊做筆記。不足之處請指教。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
第一講:方程組的幾何解釋
1. 方程組
對於方程組:
我們可以用矩陣進行表示:
係數矩陣 A,未知數向量 x,右側向量為b,則可寫成Ax=b。
1.1 行影象的理解方式
試圖將每一個完整方程所表示的影象表示出來。
交點即方程的解為(1,2)
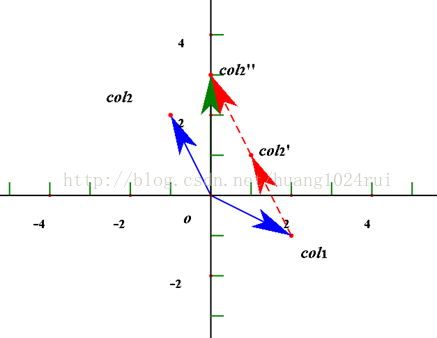
1.2 列影象的理解方式
關注矩陣的列所表示的向量,把兩個方程組放在一起考慮:
這樣做的目的是找到兩個列向量的正確的線性組合為右側向量 ,現在需要求 x,y 這兩個數值,來製造向量
(0,3),其幾何形式,影象如下
選取所有的 x 和 y,即所有的線性組合即為整個座標平面。可以求出右側任意的 b 向量。
思考的範圍擴充套件到3維:
如果以行(row)
而對應其以列(column)的形式進行展開:
其所表示的意義為三個向量的線性組合。
2.方程組解的情況
對於上面 3 維空間的例子,
保證左側矩陣不變,然後考慮所有右側向量,任意 b,是否每個 b 都有對應解?
換種說法:列的線性組合是否能覆蓋整個三維空間?
非奇異矩陣,可逆矩陣可以做到。
如果是奇異矩陣,即不可逆矩陣,在行影象中看即至少有兩個方程組所表示的平面是平行的,在列影象中
看即至少有兩個列向量是指向同一方向的(即不相互獨立,相當於同一個向量),此時,只有 b 處在這個
向量和另一個非共線向量所表示的平面內時,方程組才有解。
3. 矩陣與向量相乘的方法
3.1. 將矩陣 A 與向量 x
的相乘,看著 A 各列的線性組合,這是極力推薦的。
矩陣乘以右側列向量可看成矩陣各列向量的線性組合,結果為列向量
左側行向量乘以矩陣可看成矩陣各行向量的線性組合,結果為行向量!
3.2 以方程形式進行運算(常規的矩陣乘法)
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
第二講: 矩陣消元
本課時的目標是用矩陣變換描述消元法。核心概念是矩陣變換。
1. 消元法(Elimination)
消元法:將主對角線上的主元固定(0 不能做主元),把主元下面的元素消為 0。過程:先完成左側矩陣的消元(變成上三角矩陣 upper triangular system),再回代運算右側向量,最後即可求出解完成整個消元過程。(matlab 也是先計算左側矩陣,再回頭計算右側向量的)
1.1 消元法(success)

左側矩陣的消元過程:U 矩陣是 A 矩陣的最終消元結果,最終得到上三角矩陣(upper triangular system)
1.2 消元法(failure)
消元法失效的情況(指不能得到三個主元):當主元上為 0 時,就通過交換行將主元位置變為非 0,當通過交換行還不能解決 0 主元的時候,消元法就失效了。(不能解決 0 主元的矩陣是不可逆矩陣)。
2. 回代(back substritution)
在方程組進行消元后,想要求出其解還需進行回代這一步。為了表示方便我們仍然使用係數矩陣,同時在這裡引入新的矩陣為增廣矩陣。引入增廣矩陣的目的是為了使Ax = b中的b也隨著係數矩陣的變換而變換,從而實現回代。
上圖右側向量回代過程:A 中加入 b 列向量變成增廣矩陣,增廣就是增加的意思,增加了新列,左側矩陣消元時,右側向量也會跟著變化。c 向量是b 向量的最終結果(c is what happens tob, andU is what happens toA)
求解:將 U 和 c 代入原式子可得解,利用上面解出的Ux=c
3. Elimination matrices(消元矩陣,row 是行,column 是列)
(引入矩陣描述這些(消元步驟的)變化(消元矩陣),用矩陣語言描述整個消元過程。)
回憶下我們應該怎樣看待矩陣乘法(左行右列):
矩陣乘以列向量是矩陣列的線性組合,結果為列向量;行向量乘以矩陣式矩陣行的線性組合,結果為行向
量。
這兩張圖是重點,是做矩陣消元的基礎。
下面給一個例子:
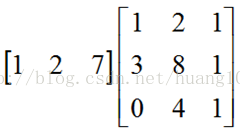

然後:
的結果是:
下面用消元矩陣來對矩陣進行消元,注意變換過程我們應該始終用線性組合的方式進行思考。同時注意到:
單位矩陣是一個不會對任何矩陣有任何變換作用的矩陣。
3.1 第一步
第一步消元:我們要對中間的矩陣進行消元,得到右側矩陣,第一步為 row2=row2-3*row1。依次考慮左側矩陣的行,第一行與中間矩陣的各個行向量進行線性組合,右側矩陣的第一個行向量就是這個線性組合的結果,可觀察容易得出左側消元矩陣第一行為(1 0 0)。其實只需要由變換(row2=row2-3*row1)可得,消元矩陣中只有第二行有不同於單位矩陣的數值,即(-3 1 0)。
E_21是elementary矩陣,對第二行第一個數進行處理。
3.2 第二步
以上每一步消元都使用到一個初等矩陣進行變換,我們將這些初等矩陣變換步驟綜合起來(為什麼綜合起
來?原因之一是更節省空間),即
4. Matrix multiplication(矩陣乘法)
4.1 逆矩陣初知
有什麼矩陣可以一次性完成 E32 和 E21 的消元任務呢?可以用結合律將 E32 和 E21 乘起來得到,但我們不這樣做。
更好的方法:不是關於 A 怎麼變換成 U,而是 U 如何變成 A,逆變換。下一課時將詳細講解。逆矩陣,右側消元矩陣表示的變換是 row2 減去 3 倍 row1,將右側向量從(2 12 2)變成(2 6 2)。現在需要將(2 6 2)通過找到某矩陣取消這次消元,減去多少就加回來多少,變回(2 12 2),即該矩陣乘以初等矩陣得到單位矩陣。
即:原矩陣是 A,E_1 A=B,E_2 E_1 A=E_2 B,A=E_2 B(E_2 會將B 變回A),I_A=E_2B,E_2 E_1=I,E_2 與E_1 互為逆矩陣。
4.2 置換(permutation)矩陣
置換(permutation)矩陣:即交換行或交換列的變換矩陣,用P表示。
行交換:
列交換:
總結:
本課的重點內容是:1. 怎樣形成上三角矩陣;
2. 左行右列的真正含義。
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
第三講:矩陣的乘法和逆矩陣(非奇異矩陣)
本課時先講解矩陣乘法運算,然後是逆矩陣及如何通過增廣矩陣求逆。
一、矩陣乘法:5種方法
A(m×n), B(n×p) =C(m×p),A 列必須等於 B 的行數,C=AB。
1.1 常規方法,行列點乘法
C=AB,C 中的第 i 行 j 列結果來自A 的第 i 行向量與 B 的第 j 列向量的點乘。整行整列的進行。即:
1.2 列方法,整列考慮,列的線性組合方式
B 的一個列向量乘以 A(矩陣A 各列向量的線性組合)得到C 的對應列向量,此過程其餘列向量暫不參與計算。即:
1.3 行方法,整行考慮,行的線性組合方式
A 的一個行向量乘以 B(矩陣 B 各行向量的線性組合)得到C的對應行向量,此過程其餘行向量暫不參與計算。
1.4 列×行法:AB 等於 A 各列與 B 各行乘積之和
A 中列乘以 B 中行,如 A 第一列乘以 B 第一行得一個矩陣(這樣的矩陣很特殊,行向量和列向量都是單個向量的線性組合,第四講會講到有關行空間,列空間的概念),最後將得到的各矩陣相加。我們就看一列和一行相乘的例子:
1.5 分塊乘法
將矩陣 A,B 分成能夠相互匹配的塊,然後對應進行分塊行點乘分塊列。
二. 矩陣的逆
2.1 定義
2.2 判定逆矩陣
1)行列式為 0。
2)列影象思考,假設 A 可逆,那 A 乘以他的逆矩陣得單位矩陣,A 矩陣乘以其逆矩陣的第一列得單位矩陣的第一列(1 0),因為其列的線性組合始終在(1 2)這條直線上,所以不可能得到(1 0)向量。
3)如果存在非 0 向量
x,使的 Ax=0,即 x 對
A 的列向量的線性組合可以得到 0 向量(有一列線上性組合中不起作用),那麼 A 是不可逆的。證明:假設存在可逆矩陣 A^-1,那麼有A^-1Ax=0,得 Ix=0,得x=0,與x是非 0 向量相違背。
結論:不可逆矩陣,奇異矩陣,其列能通過線性組合得到 0 向量。
2.3 求解矩陣的逆
1)利用列的線性組合思想,矩陣 A 乘以該求的逆矩陣得到單位矩陣,這樣,求逆和求方程組是一個意思
2)將兩個方程組放在一起考慮,如下,可理解為係數矩陣不變,分別求兩個方程組的解,即可求得矩陣的逆。我們把下面兩個放在一起考慮,形成增廣矩陣,使得消元變換對兩個方程組的作用是一樣的。將增廣矩陣的左側變換消元為單位矩陣,右側就變成其逆矩陣了。這是高斯-若爾當思想消元。
為什麼增廣矩陣的右側變成的是矩陣 A 的逆,以下變換給予證明:E 為一次性的消元矩陣,EA=I,那麼E=A^-1 了。
2.4 A 和 B 都存在逆,那麼 AB 的逆是多少?
答案是: B 的逆乘以 A 的逆得到的矩陣。為什麼相乘的順序要反過來?因為逆即是逆操作。
2.5 可逆矩陣轉置的逆是什麼?
A 乘以 A 的逆等於單位矩陣,兩側同時轉置,右側單位矩陣轉置仍然得單位矩陣,左側分別轉置兩個矩陣,
然後以相反順序相乘,因此 A 的逆的轉置乘以 A 的轉置得到單位陣。A 轉置的逆即是 A 的逆的轉置。因
此,要求 A 轉置的逆,只需要先求 A 的逆,然後求該逆的轉置即可。轉置和逆兩種乘法運算,對於單個矩
陣而已,其順序可以顛倒。
總結:
1. 矩陣乘法的五種形式。
2. 矩陣逆的定義和求法。
3. 矩陣AB的逆和A轉置的逆。
----------------------------------------------------------------------------------------------------------------------------------------------------------