前言

　　先說下目的：對在頻域計算FIR自適應濾波器，同時避免使用長濾波器時產生的大延遲的技術進行詳細的分解。即要對濾波器分塊又分段的過程進行細緻的分析。這裡假設讀者有相應的LMS自適濾波器的基礎

一、濾波器分析準備

　　先從時域LMS濾波器說起，設列向量

\[{\bf{x}}(n) = {\left[ {x(n),x(n - 1),...,x(n - M + 1)} \right]^T}\]
\[{\bf{w}}(n) = {\left[ {{w_0}(n),{w_1}(n),...,{w_{M - 1}}(n)} \right]^T}\]

　　這裡列向量長度為M。考慮通過係數為w(n)的FIR濾波器對序列x(n)濾波，用卷積運算表示為\[y(n) = \sum\limits_{i = 0}^{M - 1} {{w_i}x(n - i)} \]

　　寫成向量形式：

\[y(n) = {{\bf{w}}^T}(n){\bf{x}}(n)\]

　　簡單從公式上，初學者其實不容易理解FIR濾波器的工作過程，這裡換一種表達方式：把向量和矩陣用時間序列索引與符號來表示。應該就會比較好理解一些，對於序列：7，2，-3，-6，12，8，-7，-5，4，6。通過一個長度為4的FIR濾波器，輸入向量 隨時間序列的迭代變化表示為

\[\begin{array}{*{20}{c}}
{n = 0} \hfill & {{\bf{x}} = {{\left[ {\begin{array}{*{20}{c}}
7 & 0 & 0 & 0 \\
\end{array}} \right]}^T}} \hfill \\
{n = 1} \hfill & {{\bf{x}} = {{\left[ {\begin{array}{*{20}{c}}
2 & 7 & 0 & 0 \\
\end{array}} \right]}^T}} \hfill \\
{n = 2} \hfill & {{\bf{x}} = {{\left[ {\begin{array}{*{20}{c}}
{ - 3} & 2 & 7 & 0 \\
\end{array}} \right]}^T}} \hfill \\
{n = 3} \hfill & {{\bf{x}} = {{\left[ {\begin{array}{*{20}{c}}
{ - 6} & { - 3} & 2 & 7 \\
\end{array}} \right]}^T}} \hfill \\
{n = 4} \hfill & {{\bf{x}} = {{\left[ {\begin{array}{*{20}{c}}
{12} & { - 6} & { - 3} & 2 \\
\end{array}} \right]}^T}} \hfill \\
\end{array}\]

二、濾波器分塊處理

　　下面準備寫成時間序列索引的形式(向量各元素用時間序列對應的索引號代替，如：[0 -1 -2 -3]^T)，這樣有利於在接下來的分析中看的更清楚一些，對於矩陣，也會沿用這樣的方式。

　　先從頻域矩陣分塊處理說起，分塊方法是一種批處理方法，為了說的更清楚一些，這裡用一個示例來說明，設濾波器長度M = 6，塊長度N = 4，表示每次批處理4個單元

\[\left[ {\begin{array}{*{20}{c}}
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_0}} \hfill \\
{{w_1}} \hfill \\
{{w_2}} \hfill \\
{{w_3}} \hfill \\
{{w_4}} \hfill \\
{{w_5}} \hfill \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{y_0}} \hfill \\
{{y_1}} \hfill \\
{{y_2}} \hfill \\
{{y_3}} \hfill \\
\end{array}} \right]\]

　　觀察輸入向量組成的矩陣可以發現，這是一個Toeplitz矩陣。要轉到頻域進行處理，一個比較可行的方式是把Toeplitz矩陣轉為迴圈矩陣。再利用DFT把迴圈矩陣對角化。

　　那這個迴圈矩陣的大小是多少比較合適呢，由卷積過程可知，卷積後輸出長度為L = M + N – 1 = 9，也就是說，用M + N – 1個卷積長度完全可以表達出來，也就是說迴圈矩陣C的大小為LxL應該是足夠的。用迴圈矩陣表示如下：

\[\left[ {\begin{array}{*{20}{c}}
\hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} \\
\hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} \\
\hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} \\
\hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} \\
\hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 \\
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 & \hfill 1 \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 & \hfill 2 \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill 3 \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_0}} \\
{{w_1}} \\
{{w_2}} \\
{{w_3}} \\
{{w_4}} \\
{{w_5}} \\
0 \\
0 \\
0 \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
\times \\
\times \\
\times \\
\times \\
\times \\
{{y_0}} \\
{{y_1}} \\
{{y_2}} \\
{{y_3}} \\
\end{array}} \right]\]

　　這裡輸出向量中的X部分是迴圈卷積的結果，是要捨棄的部分。重寫以上過程

 \[{\bf{y}}(n) = P_{L \times L}^{01}C{\bf{\hat w}}(n) = P_{L \times L}^{01}{F^{ - 1}}FC{F^{ - 1}}F{\bf{\hat w}}(n)\]

　　分解為4步：

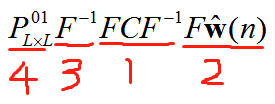
1. 是一個對角矩陣，在程式設計實現中，可以取迴圈矩陣C的第一列變換到頻域來代替
2. 是把後面補0後的濾波器係數變換到頻域
3. 是一個逆FFT變換
4. 是為了只選取最後N個做為濾波器的輸出結果，程式設計中做到這點很方便

　　再看濾波器的更新過程，這裡把步長引數省去

\[w(n + 1) = w(n) + \left[ {\begin{array}{*{20}{c}}
\hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 \\
\hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 \\
\hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 \\
\hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 \\
\hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} \\
\hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{e_0}} \\
{{e_1}} \\
{{e_2}} \\
{{e_3}} \\
\end{array}} \right]\]

　　用迴圈矩陣表示梯度向量的計算過程

\[\left[ {\begin{array}{*{20}{c}}
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
\hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 \\
\hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 \\
\hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 \\
\hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 \\
\hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} \\
\hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} & \hfill { - 2} \\
\hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} & \hfill { - 3} \\
\hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} & \hfill { - 4} \\
\hfill { - 4} & \hfill { - 3} & \hfill { - 2} & \hfill { - 1} & \hfill 0 & \hfill 1 & \hfill 2 & \hfill 3 & \hfill { - 5} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
0 \\
0 \\
0 \\
0 \\
0 \\
{{e_0}} \\
{{e_1}} \\
{{e_2}} \\
{{e_3}} \\
\end{array}} \right]\]

　　重寫濾波器係數更新公式如下： 

\[\begin{array}{l}
w(n + 1) = w(n) + P_{L \times L}^{10}{C^T}{{\bf{e}}_L} = w(n) + P_{L \times L}^{10}{F^{ - 1}}F{C^T}{F^{ - 1}}F{{\bf{e}}_L} \\
W(n + 1) = W(n) + FP_{L \times L}^{10}{F^{ - 1}}F{C^T}{F^{ - 1}}E \\
\end{array}\]

這裡W向量是濾波器係數的頻域表示。同樣做4步分解：

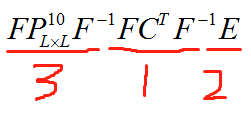
1.  仍然是一個對解矩陣，可取迴圈矩陣C的第一列變換到頻域後再取共軛來實現
2. E是把前面補0後的誤差訊號變換到頻域
3. 這步是比較麻煩的地方。如果為了計算量忽略這一步（webrtc的做法），就是不對梯度做約束，而speex是通過變換到時域再置後面部分為0來避免直接矩陣運算的，個人比較喜歡speex的實現方式。當然，由於這是一個定值，不考慮計算量的話，也可以直接在頻域進行矩陣的乘法
4. 與W(n)在頻域相加

　　至此，已經完成了濾波器分塊的頻域處理分析，但要注意的是，這裡濾波器的長度是L = M + N – 1，分塊處理轉到頻域雖然計算上方便了，但隨著時域濾波器係數長度M和分塊長度N越來越大，延時也會隨之線性增大，接下來，就著手解決這個問題。

三、對濾波器進行分割（分段）

　　當濾波器長度M很大，且使用一個比M小很多的塊長度時，可以把卷積和的運算過程分割為多個塊的和，用多個分塊濾波器的和來合成最終的結果，這樣處理就可以使濾波器的延時大幅度的縮短。以M = 8，P = 2，N = 4為例進行說明這個分割過程。也就是說，如果對一個長度M = 8的濾波器，把濾波器分成2個塊，每塊4個數據，可以把卷積過程寫為

\[\begin{array}{l}
y(n) = \sum\limits_{l = 0}^{P - 1} {{y_l}(n)} \\
{y_l}(n) = \sum\limits_{i = 0}^{N - 1} {{w_{i + lN}}x(n - lN - i)} \\
\end{array}\]

　　用矩陣的方式表示出來：

\[\left[ {\begin{array}{*{20}{c}}
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill | & \hfill { - 4} & \hfill { - 5} & \hfill { - 6} & \hfill { - 7} \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill | & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill { - 6} \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill | & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill | & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} \\
\end{array}} \right]\left[ {\frac{{\begin{array}{*{20}{c}}
{{w_0}} \\
{{w_1}} \\
{{w_2}} \\
{{w_3}} \\
\end{array}}}{{\begin{array}{*{20}{c}}
{{w_4}} \\
{{w_5}} \\
{{w_6}} \\
{{w_7}} \\
\end{array}}}} \right] \Rightarrow \begin{array}{*{20}{c}}
{\left[ {\begin{array}{*{20}{c}}
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_0}} \\
{{w_1}} \\
{{w_2}} \\
{{w_3}} \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{y_{\begin{array}{*{20}{c}}
0 & 0 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 1 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 2 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 3 \\
\end{array}}}} \\
\end{array}} \right]} \\
{\left[ {\begin{array}{*{20}{c}}
\hfill { - 4} & \hfill { - 5} & \hfill { - 6} & \hfill { - 7} \\
\hfill { - 3} & \hfill { - 4} & \hfill { - 5} & \hfill { - 6} \\
\hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill { - 5} \\
\hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_4}} \\
{{w_5}} \\
{{w_6}} \\
{{w_7}} \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{y_{\begin{array}{*{20}{c}}
1 & 0 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
1 & 1 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
1 & 2 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
1 & 3 \\
\end{array}}}} \\
\end{array}} \right]} \\
\end{array}\]

\[\begin{array}{*{20}{c}}
{{y_0} = {y_{\begin{array}{*{20}{c}}
0 & 0 \\
\end{array}}} + {y_{\begin{array}{*{20}{c}}
1 & 0 \\
\end{array}}}} \\
{{y_1} = {y_{\begin{array}{*{20}{c}}
0 & 1 \\
\end{array}}} + {y_{\begin{array}{*{20}{c}}
1 & 1 \\
\end{array}}}} \\
{{y_2} = {y_{\begin{array}{*{20}{c}}
0 & 2 \\
\end{array}}} + {y_{\begin{array}{*{20}{c}}
1 & 2 \\
\end{array}}}} \\
{{y_3} = {y_{\begin{array}{*{20}{c}}
0 & 3 \\
\end{array}}} + {y_{\begin{array}{*{20}{c}}
1 & 3 \\
\end{array}}}} \\
\end{array}\]

　　接下來再分別把這兩個分割出來的NxN矩陣塊分別轉換為迴圈矩陣的形式。（這裡只寫出第一個，第二個塊有興趣的朋友自己推吧）

\[\left[ {\begin{array}{*{20}{c}}
\hfill { - 3} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} \\
\hfill { - 2} & \hfill { - 3} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} \\
\hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 \\
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill 3 & \hfill 2 & \hfill 1 \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill 3 & \hfill 2 \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill 3 \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_0}} \\
{{w_1}} \\
{{w_2}} \\
{{w_3}} \\
0 \\
0 \\
0 \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
\times \\
\times \\
\times \\
{{y_{\begin{array}{*{20}{c}}
0 & 0 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 1 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 2 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 3 \\
\end{array}}}} \\
\end{array}} \right]\]

　　這樣就可以方便的轉到頻域進行處理，再把每塊的處理結果相加，就完成了分段分塊的頻域卷積運算。濾波器的係數更新也是同理

　　另外，雖然2N-1個長度的頻域復向量足以完成必要的卷積過程，實際演算法中FFT長度通常取2N，這樣計算更方便，這時分割後的第一個塊的迴圈矩陣如下所示：

\[\left[ {\begin{array}{*{20}{c}}
\hfill { - 4} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} \\
\hfill { - 3} & \hfill { - 4} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} \\
\hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} \\
\hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 \\
\hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill 3 & \hfill 2 & \hfill 1 \\
\hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill 3 & \hfill 2 \\
\hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} & \hfill 3 \\
\hfill 3 & \hfill 2 & \hfill 1 & \hfill 0 & \hfill { - 1} & \hfill { - 2} & \hfill { - 3} & \hfill { - 4} \\
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{w_0}} \\
{{w_1}} \\
{{w_2}} \\
{{w_3}} \\
0 \\
0 \\
0 \\
0 \\
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
\times \\
\times \\
\times \\
\times \\
{{y_{\begin{array}{*{20}{c}}
0 & 0 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 1 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 2 \\
\end{array}}}} \\
{{y_{\begin{array}{*{20}{c}}
0 & 3 \\
\end{array}}}} \\
\end{array}} \right]\]

　　另一個分割塊也是同理，這裡不再詳細列出來，有興趣的朋友可以自己手畫一遍玩玩，上圖有一個小細節的哦，迴圈矩陣的對角元素可以是任意的，不影響最終效果，但通常大家都取前一個塊的第一個元素。

　　剩下的活，就是前面轉到頻域的處理過程了，不再詳述。

　　最後還有一個問題，是不是分割（段）越多越好，也不再詳細分析了，直接給出結果：不是分割數P越大越好。由於分割過程改變了輸入向量，也就改變了輸入向量相關矩陣特徵值的擴散度（條件數）。當P越大時，特徵值的擴散度就越大，演算法收斂就越慢，也更容易出現發散的可能。

參考文獻：

1. Advances in Network and Acoustic Echo Cancellation
2. Adaptive Filters Theory and Applications Second Edition
3. Adaptive Signal Processing Applications to Real-World Problems