本篇將舉三個重要的理論或領域，以展示之前訊號理論的應用和意義。其中濾波理論和通訊系統是非常大的應用領域，這裡僅對基礎的概念和方法做個介紹，以作入門之用。

1. 濾波系統

1.1 濾波器

　　在系統函式的性質中，我們看到訊號在時域上的微分、積分、卷積等複雜運算，在頻域都變成了代數運算。這說明分析和使用訊號的頻域，有其天然的優勢，也會帶來更廣泛的應用。當然，頻域的操作最終都體現在時域上，注意討論其相互關係和平衡，有時也是必需的。濾波系統主要就是以訊號的頻域為操作物件，具體來說就是調整不同基波的波幅、相位，以使輸出訊號滿足具體需求，這樣的系統也叫濾波器（Filter）。

　　在討論具體濾波器之前，有必要先說清楚系統對訊號的頻域究竟產生了什麼影響。訊號的頻譜系數\(X(j\omega)\)是一個復值函式，模\(|X(j\omega)|\)表示基波峰谷的高度，它稱為頻譜的幅度；角度\(\sphericalangle X(j\omega)\)表示基波初始位置，它稱為頻譜的相位。LIT系統就是將訊號的頻譜乘上了系統函式\(H(j\omega)\)，把影響按幅度和相位分開講，\(|H(j\omega)|\)稱為系統的增益（gain），\(\sphericalangle H(j\omega)\)叫系統的相移（phase shift）。

　　將頻譜的幅度、相位分開展示的座標圖（橫座標為\(\omega\)）叫模-相圖，根據對稱性，它們僅需顯示正頻率部分。為了展示更多的基波頻率，以及在系統中經常出現\(\log_{10}\omega\)，橫座標一般用對數值。另外，從圖中表示相移對相位的影響是簡單的，只需在相位上增加相移即可。為了讓增益的影響也同樣直觀，一般把幅度座標用對數表示，改乘法為加法。其實在現實中，人們對幅度的感知也是對數形式的，比如音量和功率\(\log_{10}|X|^2\)成正比。一般把\(\log_{10}|X|^2\)的單位叫做Bel，更常用的單位分貝（dB）是其十分之一，也即模座標的值是\(20\log_{10}|X(j\omega)|\)。使用以上所有方法的圖示稱為Bode圖。

　　濾波器一般通過修改幅度的方法，選擇性保留部分頻率的基波、而削弱其它頻率的基波，增益恆為\(1\)的叫全通系統。根據保留頻率的不同，有很多直觀的術語，這裡就不一一闡述了，比如低通/高通/帶通濾波、以及濾波的截止頻率/通帶/阻帶。另外，系統的相移會造成基波的時移，這在關心時移的場景裡（比如圖片），同樣是不可忽略的影響。所有不期望發生的增益和相移，都被稱為訊號的失真。根據訊號時移的性質，相同的時移\(t_0\)對應相移\(\omega t_0\)，相移要和頻率成正比訊號才不失真，\(t_0\)稱為系統的群時延。在一般系統的區域性，也有近似的群時延\(\tau(\omega)\)（式（1））。

\[\sphericalangle H(j\omega)=\omega\cdot\tau(\omega)+\phi(\omega),\;\;\tau(\omega)=\dfrac{\text{d}[\sphericalangle H(j\omega)]}{\text{d}\,\omega}\tag{1}\]

1.2 濾波函式

　　理想的濾波器的系統函式只有\(0\)和\(1\)兩種值，這裡就舉例不同場景的低通濾波，高通/帶通濾波可由其轉變而來。為方便敘述，先定義方波函式\(U_T(x)\)，它僅在\(|x|\leqslant T\)時取\(1\)。如果設低通濾波器\(X(j\omega)\)為\(U_W(\omega)\)，不難得到其單位衝激響應\(x(t)\)（式（2）左）。你可以記憶\(\text{sinc}\,\pi t\overset{F}{\leftrightarrow}U_{\pi}(\omega)\)，另外在\(t=0\)處就取周邊極限值。利用對偶性，就可以得到方波衝激響應的系統函式（式（2）右）。

\[\dfrac{\sin Wt}{\pi t}\;\overset{F}{\leftrightarrow}\;U_W(\omega);\;\;U_T(t)\;\overset{F}{\leftrightarrow}\;\dfrac{2\sin T\omega}{\omega}\tag{2}\]

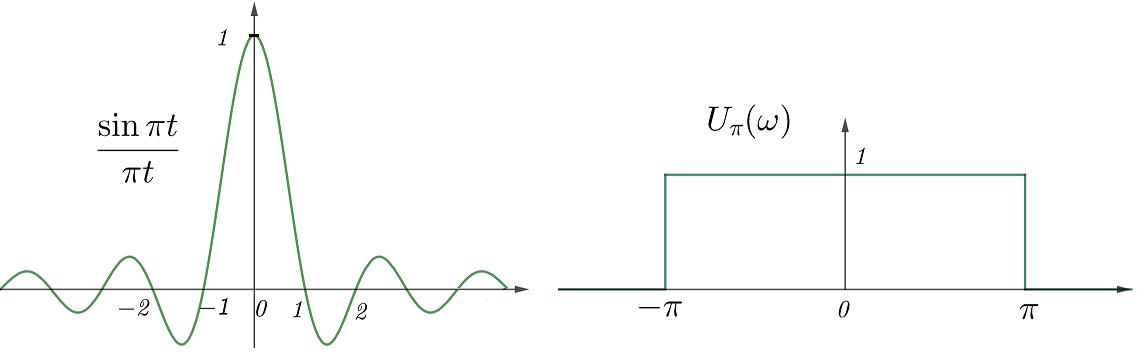
　　如果記\(\text{sinc}(t)=\sin t/t\)，則式（2）左就是\(W\text{sinc}(Wt)/\pi\)。對於比較大的\(W\)，它就是\(\text{sinc}(t)\)的橫向壓縮以及縱向拉昇，且能量都集中在原點附近。當\(W\to\infty\)時，可知左式在\(t=0\)處趨於無窮，利用三角積分的值還能算得原點附近的積分趨於\(1\)。這非常類似\(\delta(t)\)，其實\(W\to\infty\)時\(U_W(\omega)\)是全通濾波，故它的單位衝激響應就是\(\delta(t)\)（即恆等變換）。同樣道理，式（2）右中\(T\to\infty\)時的系統函式近似\(2\pi\delta(\omega)\)，這與周期函式的FT相一致。

　　為討論離散訊號，對於週期\(T\)，先定義週期方波\(U_{\theta}(x)\)，它僅在\(|x-kT|\leqslant \theta T/2\)時為\(1\)。對離散訊號的FT，設低通濾波器\(X(j\omega)\)為\(U_{\theta}(\omega)\)，不難得到其單位脈衝響應\(x(t)\)（式（3）左），其中\(a_0=\theta\)。濾波\(U_{\theta}(\omega)/(2\theta\pi)\)每個週期的積分恆為\(1\)，當\(\theta\to 0\)時即為單位衝激串，左邊恆有極限\(1/(2\pi)\)，與定值的FT一致。然後利用對偶性，也能得到週期方波的FS（式（3）右），以及單位衝激串的FS恆為\(1/T\)。最後還有離散方波的FT，以及週期離散方波的FS（式（4）），這裡暫不考慮FS上的濾波。

\[\dfrac{\sin(n\theta\pi)}{n\pi}\;\overset{F}{\leftrightarrow}\;U_{\theta}(\omega);\;\;U_{\theta}(t)\;\overset{FS}{\leftrightarrow}\;\dfrac{\sin(k\theta\pi)}{k\pi}\tag{3}\]

\[U_{n_0}(n)\;\overset{F}{\leftrightarrow}\;\dfrac{\sin[\omega(n_0+1/2)]}{\sin(\omega/2)};\;\;U_{\theta}[n]\;\overset{FS}{\leftrightarrow}\;\dfrac{\sin(k\theta\pi)}{N\sin(k\pi/N)}\tag{4}\]

　　一個濾波器不光要考慮頻域的效果，還要顧及時域帶來的特性，一般用單位階躍響應考察濾波器的時域特徵。它逐步收斂於單位衝激響應的極限值，收斂過程中，有幾個引數比較影響系統的好壞。首先上升到穩態的時間，表示系統響應的快慢（或當前訊號對後續輸出的影響大小），一般越快越好。然後還有進入穩態前的超量（超出穩定值）、以及進入穩態時的震盪，它們都影響了系統的穩定速度，可能降低系統實時性。

　　式（2）左的理想濾波不光有超量和震盪，現實中還很難實現（不是有理系統），另外還需要整個輸入訊號才行（非因果系統），實際上很少使用。非理想濾波在通帶和阻帶之間沒有明顯的界限，而是有一定長度的過渡帶，並且通帶/阻帶上都可能有一些起伏，以此可以換來時域更好的特性。一般越小的過渡帶、越小的起伏，會帶來更大的超量和震盪、以及更長的上升時間，使用中需要注意平衡。更多具體的濾波要到後續課程中討論了。

2. 取樣定理

2.1 取樣與插值

　　離散時間訊號更方便處理，經常要把連續訊號\(x(t)\)取樣成離散序列\(x[nT]\)，為此需要從理論上分析這兩種訊號的關係。首先自然地想把取樣表示成\(x(t)s(t)\)，其中\(s(t)\)僅在\(t=nT\)處有非零值\(1\)，但由於\(s(t)\)沒有正常的分析性質（微積分），頻域分析無法進行。為此可以把\(s(t)\)換成單位衝激串函式\(p(t)\)（式（5）左），上一節已經知道它的FS頻譜是\(1/T\)，故它的FT頻譜系數是式（5）右（\(\omega_s=2\pi/T\)）。

\[p(t)=\sum_{k\in\Bbb{Z}}\delta(t-kT)\;\overset{F}{\leftrightarrow}\;P(j\omega)=\omega_s\sum_{k\in\Bbb{Z}}\delta(\omega-k\omega_s)\tag{5}\]

　　記取樣訊號為\(x_p(t)=x(t)p(t)\)，根據乘法性質知其頻譜系數為\(X_p(j\omega)=\dfrac{1}{2\pi}X(j\omega)*P(j\omega)\)。式（5）帶入便知，\(X_p(j\omega)\)是多個\(X(j\omega)*\delta(\omega-k\omega_s)/T\)的累加，而後者是\(X(j\omega)/T\)平移\(k\omega_s\)得到，故\(X_p(\omega)\)就是\(X(j\omega)/T\)以\(\omega_s\)為週期的疊加。如果\(x(t)\)的頻寬滿足\(\omega_c<\omega_s\)，它們在\(X_p(j\omega)\)中的疊加不會出現混疊，可以用低通濾波完整截取出來。也就是說從\(x_p(t)\)中可以完全恢復出\(x(t)\)，這個結論稱為取樣定理。

　　取樣定理是個理想化的模型，首先衝激串函式根本無法生成，其次理想濾波器也很難實現，但它從理論上說明了，足夠密度的取樣是可以儲存特定訊號的所有資訊的。需要說明的是，帶限訊號往往表現出一定平滑性，但反過來平滑訊號卻不一定是、甚至很少是帶限的（平滑不是來自低頻正弦函式）。但這並不妨礙取樣定理的實用性，一般訊號的高頻部分都足夠小，高密度的取樣可以獲得訊號的大部分資訊，足以近似恢復出原訊號。當\(\omega_c>\omega_s\)時，訊號恢復會出現不可預知的結果，比如對訊號\(\cos\omega_0 t\)低速度取樣時，恢復訊號的頻率總會下降到\(|\omega_s-k\omega_0|\)（自行證明），這個可以解釋視訊中風扇倒轉的現象。

　　現在就來討論從取樣函式\(x_p(t)\)恢復出\(x(t)\)的一般性方法，這裡\(x_p(t)\)是個數學工具，它代表了取樣資訊\(x[nT]\)。記恢復系統的單位衝激響應為\(h(t)\)，則恢復訊號\(x_r(t)\)為式（6）。不難看出，滿足\(h(0)=1,h(nT)=0,(n\ne 0)\)的系統都能準確恢復出取樣值\(x[nT]\)，這時的\(x_r(t)\)就好像\(x[nT]\)的內插函式。取樣定理中的低通方波就滿足插值條件，其它恢復訊號的插值法也要滿足插值條件，而且在頻譜上都是低通方波的一種近似，即便只是粗略的近似。

\[x_r(t)=x_p(t)*h(t)=\sum_{n\in\Bbb{Z}}x(nT)h(t-nT)\tag{6}\]

　　把式（6）看成\(x(nT)\)影響的疊加，選擇適當的\(h(t)\)便可以構造不同的恢復系統。比如記\(h_0(t)\)僅在\([0,T)\)上有非零值\(1\)，這時\(x_r(t)\)在\([nT,(n+1)T)\)上的值都是\(x(nT)\)，這樣的階梯函式叫取樣的零階保持。為了讓恢復訊號連續，最簡單的就是線性插值（相鄰兩點直線相連，也叫一階保持），不難得知\(h(t)\)是一個\((-T,T)\)上面的三角形函式。類似地可以有更平滑的高階保持，那裡\(h(t)\)要更平滑，每個點的影響範圍也更大。

2.2 數模轉換

　　連續訊號（也叫模擬訊號（analog））離散化的優點並不僅限於儲存和傳輸，數字（digital）訊號的在處理上有更多有效便捷的方法。所以經常會把模擬訊號先做個模-數轉換（A/D），通過數字訊號處理（DSP）後，再進行數-模轉換（D/A）輸出模擬訊號。在這個過程中，要想使用統一的FT理論就非常困難了，而不得不直接尋找連續FT和離散FT之間的關係，也即衝激取樣\(x_p(t)\)能否由脈衝取樣\(x_d[n]=x[nT]\)替代。

　　把\(x_p(t)\)看成衝激串的疊加，並根據\(\delta(t-nT)\)的（連續FT）頻譜，可得到\(x_p(t)\)的頻譜為式（7）左。然後直接用離散FT的公式，可得到\(x_d[n]\)的頻譜為式（7）右，這裡的\(X_d(e^{j\omega})\)已經展開為周期函式。這兩個頻譜系數雖然來自不同的變換，但卻有式（8）左的聯絡，\(X_d(e^{j\omega})\)是\(X_p(j\omega)\)在橫軸拉昇\(T\)倍，使週期成為\(2\pi\)。這個結論不僅說明了\(x_p(t)\)和\(x_d[n]\)在資訊量上的等價性，還是連續頻譜和離散頻譜之間的橋樑。

\[X_p(j\omega)=\sum_{n\in\Bbb{Z}}x(nT)e^{-j\omega nT};\;\;X_d(j\omega)=\sum_{n\in\Bbb{Z}}x(nT)e^{-j\omega n}\tag{7}\]

\[X_p(j\omega/T)=X_d(e^{j\omega});\;\;H(j\omega)=H_d(e^{j\omega T}),\,(|\omega|<\omega_p/2)\tag{8}\]

　　假設\(x_d[n]\)經過系統\(H_d(e^{j\omega})\)後變成\(y_d[n]\)，再把它衝激取樣化為\(y_p(t)\)，不難求得最後的頻譜是\(Y_p(j\omega)=X_p(j\omega)H_d(e^{j\omega T})\)，這就好比\(x_p(t)\)通過了連續系統\(H_d(e^{j\omega T})\)。如果回到連續函式，相當於\(x(t)\)經過連續系統\(H(j\omega)\)（式（8）右）後變成了\(y(t)\)，這就說明了數字訊號處理對連續系統的影響。當然還要強調一下，要想\(H(j\omega)\)等價於原離散系統，還要求\(x(t)\)是帶限的（否則只是近似系統）。更進一步講，帶限連續訊號脈衝取樣並通過離散LIT系統後，就相當於通過了一個連續LIT系統。

　　這個結論其實更適合反過來用，由於連續訊號有更好的分析性質，那些在離散訊號上“無意義”的概念（比如微分），可以先在連續訊號上設計系統，再通過式（8）得到對應的離散系統。比如連續訊號的微分器是\(H(j\omega)=j\omega\)，那麼其取樣訊號的微分器\(H_d(e^{j\omega})\)就是\(j\omega/T\)在\(|\omega|<\pi\)上的週期拓展。再比如時移系統的微分器是\(e^{-j\omega t_0}\)，其取樣訊號的微分器就是\(e^{-j\omega t_0/T}\)在\(|\omega|<\pi\)上的週期拓展。它們的單位脈衝響應可以用逆變換計算，也可以通過特殊訊號的響應直接求得。函式\(\text{sinc}(\pi t)\)在整數點上的取樣就是單位脈衝（注意此時\(T=1\)），且頻寬\(2\pi=\omega_s\)剛好沒有混疊，對它做變換（比如微分、時移）再在整數點取樣，即可得到離散系統的單位脈衝響應。

2.3 抽取和內插

　　對於高頻取樣的訊號，實際使用時往往不需要這麼高的精度，或者資料量相對資訊量是有冗餘的，這時就需要考慮離散訊號的抽取（減取樣）。記脈衝串\(p[n]\)僅在\(n=kN\)時有非零值\(1\)，易知它的頻譜系數為式（9），其中\(\omega_s=2\pi/N\)。同樣用週期卷積分析\(x_p[n]=x[n]p[n]\)的頻譜，它是\(X(e^{j\omega})/N\)以\(\omega_s\)為週期的疊加，\(2\pi\)內共有\(N\)個。當\(x[n]\)的頻寬滿足\(\omega_c<\omega_s\)時，從\(x_p[n]\)可以完全恢復出\(x[n]\)。以及把抽取值重組為訊號\(x_b[n]=x_p[nN]\)，根據縮放性質可有關係式\(X_b(e^{j\omega})=X_p(e^{j\omega/N})\)，兩者在資訊量上是等價的。

\[p[n]=\sum_{k\in\Bbb{Z}}\delta[n-kN]\;\overset{F}{\leftrightarrow}\;P(e^{j\omega})=\omega_s\sum_{k\in\Bbb{Z}}\delta(\omega-k\omega_s)\tag{9}\]

　　對比\(x[n]\)和\(x_b[n]\)的頻譜，後者相當於前者在每個\(2\pi\)內拉伸\(N\)倍（同時幅值降低到\(1/N\)）。以上過程的逆過程，即先拉昇補零再方波擷取，可以看成是把\(x_b[n]\)內插（增取樣）成\(x[n]\)，同時頻譜收縮\(N\)倍。我們希望減取樣的頻譜能正好填滿週期\(2\pi\)，以充分利用頻譜而降低取樣資料量，這個過程往往需要先增取樣，以使\(2\pi/\omega_c\)儘量接近整數。另外，縮放的過程也許可以更直觀地解釋式（5）和（9），\(x_b[n]\)完整擁有\(x[n]\)的頻譜，\(x_p[n]\)本質上是個延展函式，延展過程中其它週期的頻譜都被壓縮至\(2\pi\)內。式（9）則可以解釋成，無窮處的頻譜被壓縮至實軸內了。

3. 通訊系統

3.1 基本概念

　　現代通訊是以電磁波為資訊載體的，在空氣中波長越長（頻率越低），無線電波的傳播距離越遠（速度同光速）；而高頻部分頻寬更寬，可以容納更多的資訊。在工業上，長波（0~300kHz）可傳播國際廣播，中波（300k~3MHz）多用於AM，短波（3m~300MHz）多用於高保真傳輸（比如FM廣播、手機通訊、Wifi等）。各種不同的訊號想要通過電磁波傳輸，就必須把資訊“嵌入”到一個高頻訊號中，前者稱為調製訊號、後者稱為載波訊號，嵌入和解析訊號的方法分別叫調製和解調。

　　載波訊號多為正弦波，根據載波被修改的內容，調製方法和大致分為幅度調製（AM）和頻率調製（FM）。頻率調製直接修改載波的頻率\(\omega_c\)（式（10）），由於FM使用的高頻，區域性的頻率\(\omega_c+kx(t)\)近乎不變，可由此解調出\(x(t)\)。頻率幾乎不會衰減，因此FM可以高保真傳輸資訊，缺點則是需要佔用較大的頻寬。幸好高頻的頻寬足夠寬，甚至可以劃分為多個頻段，以供多路FM訊號傳輸，這個方法就叫頻分多路複用（FDM）。

\[A\cos\theta(t),\;\;\dfrac{\text{d}\theta(t)}{\text{d}t}=\omega_c+kx(t)\tag{10}\]

　　幅度調製直接把調製波乘上載波，週期載波的頻譜是可數個衝激串，根據乘法性質可知，調製後的頻譜是原頻譜的平移疊加，可使用帶通濾波解調出來。一類常用的AM載波是週期方波，方波無需持續很久、而只要頻率夠高，即可傳輸近似的訊號。效果相當於是高頻、有短暫持續的取樣，也被叫做脈衝幅度調製（PAM）。另外可想而知，一個取樣週期內可以有多路訊號並存，這個方法就叫時分多路複用（TDM）。

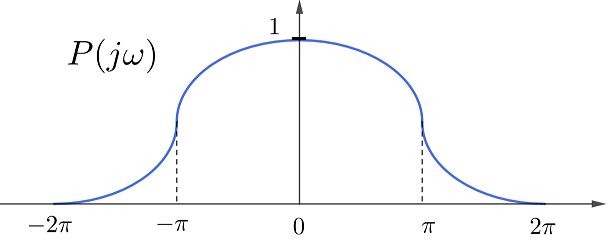
　　值得注意的是，PAM所使用的方波載波，其頻譜是無限的，在傳輸中必定會失真。而失真的訊號在TDM中會造成碼間干擾，導致所有訊號都變形。為此PAM的載波要選擇特殊的週期脈衝，它是帶限的、並在其它通道時間上還是過零的。為討論方便，把PAM的時隙設為\(1\)，脈衝\(p(t)\)要在\(k\ne 0\)上過零，即頻譜\(P(j\omega)\)有界且\(P(j\omega)e^{-jk\omega}\)的積分為零。假定脈衝對稱、並利用三角函式的性質，可以構造如式（11）的頻譜函式，其中最有代表性的是方波\(U_{\pi}(\omega)\)，它的脈衝函式是\(\text{sinc}\,\pi t\)。當然如果把脈衝數據都數字化（二進位制），也就沒有碼間干擾的問題了，它被稱為脈衝編碼調製（PCM）。

\[P(j\omega)=P(-j\omega);\;\;P(j\omega)+P(j(2\pi-\omega))=1,\;(0\leqslant\omega\leqslant\pi)\tag{11}\]

3.2 正弦幅度調製

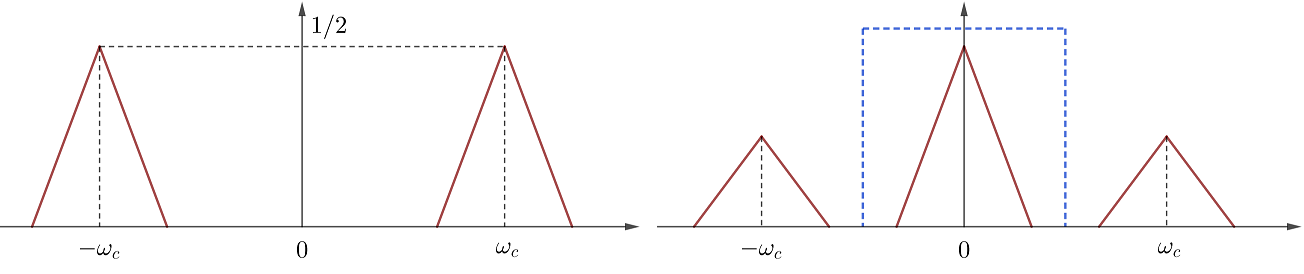
　　幅度調製更常用的載波還是正弦函式，它更易於產生，也有更好的分析性質和頻譜系數。AM的主要目的是要把訊號嵌入到某個傳輸頻段，比較自然地可以想到頻域的平移性質，即如式（12）用覆載波\(e^{j\omega_c t}\)將\(X(j\omega)\)整體右移\(\omega_c\)。在接收端，只需用覆載波\(e^{-j\omega_c t}\)即可解調出\(x(t)\)，覆載波可以用兩路訊號\(x(t)\cos\omega_c t\)和\(x(t)\sin\omega_c t\)來表示。如果只想使用單通道也是可以的，式（13）表明載波\(\cos\omega_c t\)將\(X(j\omega)\)產生了兩份疊加。接收端如果還用\(\cos\omega_c t\)解調，便可以得到右圖中的三份頻譜，使用低通濾波器即可保留單個\(x(t)\)的頻譜。

\[x(t)e^{j\omega_c t}\;\overset{F}{\leftrightarrow}\;X(j(\omega-\omega_c))\tag{12}\]

\[x(t)\cos\omega_c t\;\overset{F}{\leftrightarrow}\;\dfrac{1}{2}[X(j(\omega-\omega_c))+X(j(\omega+\omega_c))]\tag{13}\]

　　在實現中還有一個棘手的問題需要解決，即調製載波和解調載波（不論是單雙通道）需要是同相的，這稱為同步解調，需要較高的成本。而現實中兩者往往有相位差\(\phi(t)\)，並且隨時間不穩定地變化。如果使用的是覆載波，解調出來的訊號其實是\(x(t)e^{j\phi}\)，在\(x(t)\)恆為正的情況下，取其範數即可得到\(x(t)\)。為了讓調製波恆為正，有時需要將波幅同步提升，這將帶來額外的功率消耗。如果使用的是正弦載波，解調的訊號將是\(x(t)\cos\phi t\)，好像無計可施了。其實如果\(x(t)\)恆為正、且\(\omega_c\)足夠大，\(x(t)\cos\omega_c t\)的所有波峰就好像是對\(x(t)\)的取樣（使用包絡檢測器），從它們也可以恢復出\(x(t)\)的近似值。

　　正弦載波調製佔用了\(x(t)\)兩倍量的頻寬，這對有限的頻寬是一種浪費，它稱為雙邊帶調製（DSB）。\(x(t)\)的頻譜按\(\omega\)的正負分為兩個邊帶，調製後靠近原點的兩個分支叫下邊帶（否則叫上邊帶），僅保留上/下邊帶的調製稱為單邊帶調製（SSB）。SSB需要用理想帶通濾波實現，我們知道這個難以實現。其實利用兩個頻譜分支的平移對稱性、以及三角函式的對稱性，可以設計出式（14）的調製系統（90度相移網路），請自行證明它僅保留了上邊帶（以及設計保留下邊帶的系統）。

\[x(t)\cos\omega_c t+x_h(t)\sin\omega_c t,\;\;x_h(t)\;\overset{F}{\leftrightarrow}\;jX(j\omega)\cdot\text{sign}\omega\tag{14}\]

　　離散訊號的幅度調製非常類似，可以用覆載波\(e^{j\omega_c n}\)將頻譜移向高頻，然後用\(e^{-j\omega_c n}\)解調。如果用正弦函式調製，也會產生正負兩個頻譜分支，這時需要防止不同週期上頻譜的混疊。記訊號頻寬為\(\omega_m\)，首先要讓兩個分支分開，即要\(\omega_c>\omega_m/2\)；然後週期間也不能混疊，即要\(\omega_c+\omega_m/2<\pi\)。綜合便要求式（15）成立，這就要求\(\omega_m\)越小越好。其實在之前的取樣理論中我們知道，只要對訊號增取樣，即可壓縮訊號的頻譜。

\[\omega_m<2\omega_c<2\pi-\omega_m\tag{1