​

導讀：
3D點雲配準是計算機視覺的關鍵研究問題之一，在多領域工程應用中具有重要應用，如逆向工程、SLAM、影象處理和模式識別等。點雲配準的目的是求解出同一座標下不同姿態點雲的變換矩陣，利用該矩陣實現多視掃描點雲的精確配準，最終獲取完整的3D數字模型、場景。本質上，關於六自由度(旋轉和平移)的3D點雲配準問題是典型的非凸優化問題，其目標函式在六維可行域空間中具有多個波峰波谷，即優化求解過程中受初始變換矩陣影響，容易陷入區域性最優解。點雲配準結果雖然受限於其初始位置，但是早期的一些區域性的配准算法對解決點雲配準問題具有重要的應用、啟示意義。因此，本文重點介紹一些魯棒性或效率較好的區域性、全域性3D點雲配准算法。

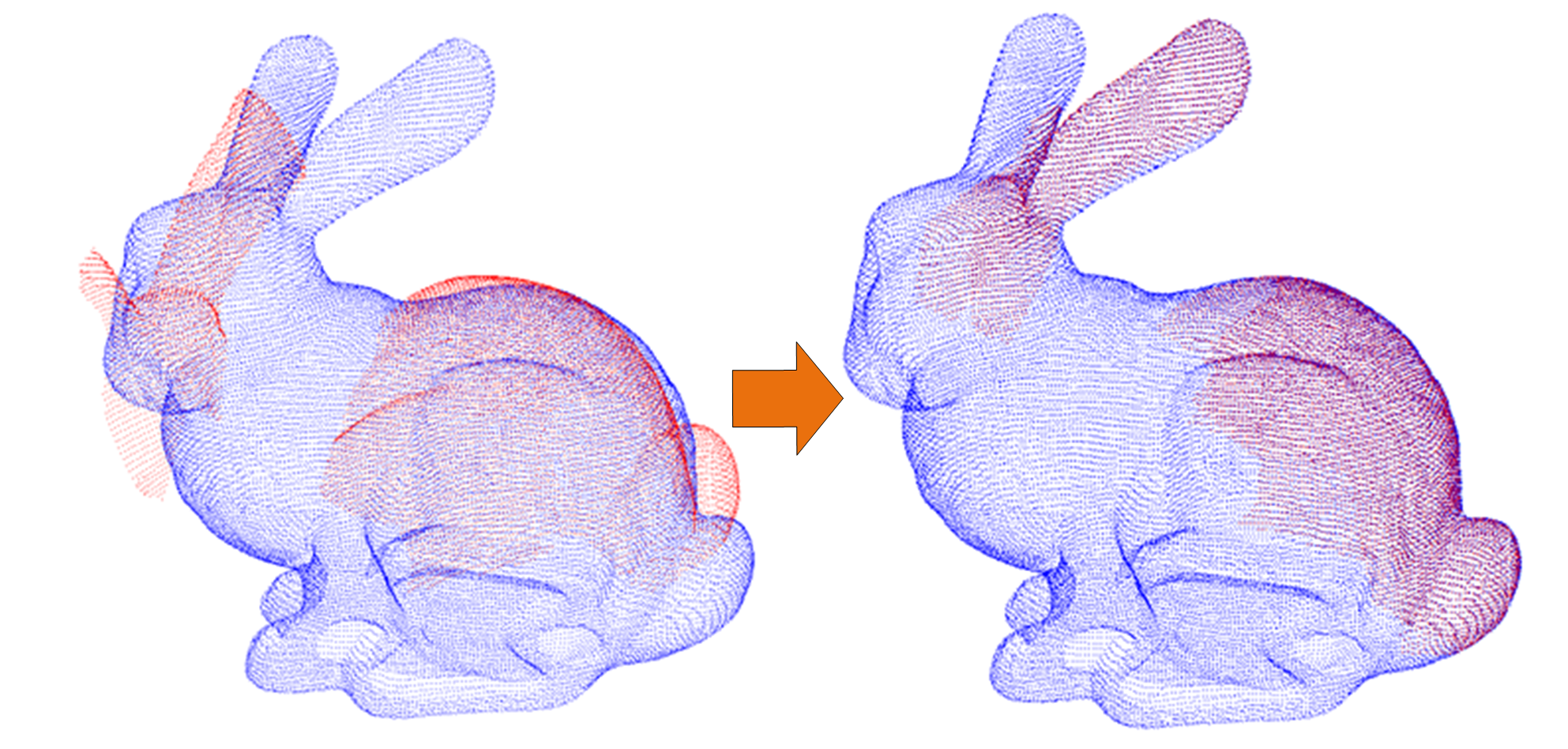
--區域性的3D點雲配准算法--

ICP（Iterative Closest Point）演算法是應用最廣泛的3D點雲配准算法之一, 其通過歐式變換求解出兩片點雲的旋轉平移矩陣及對應的配準誤差。
ICP演算法的核心思想可以簡述為:假設資料點雲 。向源點雲 移動配準，ICP演算法通過不斷求解估計的變換矩陣，直到RMSE(Root Mean Square Error)配準誤差收斂於區域性最優解 (每一次迭代過程可以描述為：在 中搜索關於 的最近鄰點集，構造協方差矩陣，奇異值分解獲得單位四元數，進而求解旋轉矩陣，平移向量則由對應點雲的質心確定，由此實現資料點雲的旋轉平移變換)。其中，關於RMSE的配準模型可以表示為：

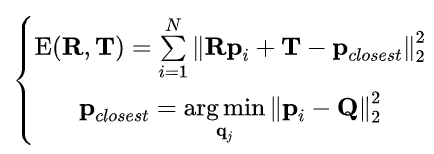
在對旋轉、平移可行域進行引數化的前提下，關於 範數配準模型的點雲配準問題可以轉化為關於旋轉和平移的非凸優化問題。ICP雖然具有簡單、收斂性好等優點，但其受限於點雲初始位置且在解決具有離群值的點雲配準問題，容易陷入區域性最優解。
為了提高ICP演算法的魯棒性，學者提出了一系列的變種ICP演算法。LM-ICP演算法提出利用Levenberg-Marquardt演算法對ICP配準模型進行求解，並利用DT（Distance-Transform）演算法替代KD-tree搜尋最近鄰點時，減小點雲初始位置對其配準結果的影響，並提高了配準效率。Chetverikov等。在ICP演算法的基礎上，提出了魯棒性更好、更實用的Trimmed ICP 演算法，對每次迭代匹配得到的最近鄰點進行篩選，即對兩兩估計的匹配點的歐式距離進行排序，摒棄其中距離較大的點集，懲罰的百分率由核函式動態計算。Trimmed ICP 演算法應用於具有離群值、噪聲的點雲配準問題時，能獲得良好的配準精度。然而，高佔比的離群值對點雲配准算法的魯棒性要求仍然是巨大的挑戰。Bouaziz等提出Sparse ICP演算法利用稀疏表示理論對進一步改進ICP演算法的魯棒性，即在 範數配準模型上增加p範數的懲罰項，提高每次迭代中求解匹配點的準確性，但其利用增廣拉格朗日求解大規模點雲配準問題時效率較差。Mavridis等結合模擬退火演算法提出了更為高效的Efficient Sparse ICP演算法，加速點雲配準的收斂速度。

為了進一步提高配準效率，Li等利用CAD模型的三角切片性質，高效求解最近鄰點，保證了配準精度，並進一步提出動態步長試探性配準，避免收斂曲線出現震盪。但實際掃描點雲的分佈並非均勻，基於CAD 模型的配準方法僅適用性於理想點雲配準問題。Zhu等通過設定硬、軟指標實現點雲的高效精確配準，即在每次迭代過程中利用雙向匹配的方式對噪聲及離群值進行懲罰。但是配準結果受限於核函式中引數的預設值。上述基於 範數的迭代最近點配准算法主要包括ICP演算法及其變種演算法，該類區域性的配准算法受限於點雲初始位置，僅適用於小角度錯開的點雲配準問題。在人機互動獲得較好點雲初始位置的前提下，迭代最近點演算法在解決點雲配準問題時具有良好的魯棒性，但也存在一些可以繼續優化的不足，可以總結為三點：
（一）受限於主成分分析、奇異值分解演算法，迭代最近點演算法雖然具有良好的收斂性，但其迭代次數較多，後期收斂緩慢。
（二）受限於資料結構，迭代最近點演算法在每次迭代過程中搜索最近鄰點的成本較高，KD-tree雖然搜尋效率較高，但仍無法滿足於解決大規模點雲的配準問題。
（三）受限於點雲的稀疏特性，並且實際應用中主要通過對點雲進行下采樣以提高配準效率，迭代最近點演算法無法實現精確配準。
針對上述不足點，學者區別於迭代最近點的配准算法構建新的配準模型，如概率密度模型、隱式最小二乘函式和高斯混合模型等，並結合其它優化演算法提高點雲配準的效率和精度。Biber等基於概率密度模型提出了Normal Distribute Transform（NDT）演算法，即使用D維的高斯函式作為配準模型：

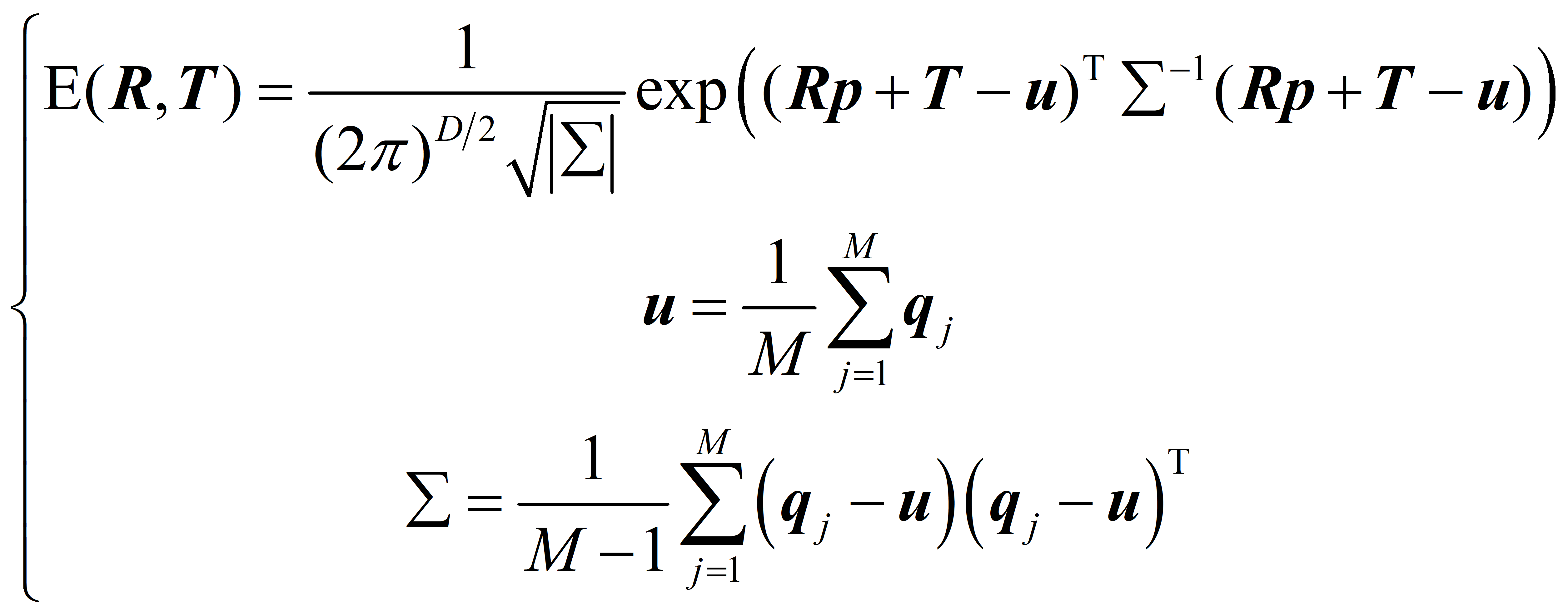
NDT演算法通過對源點雲Q進行體素劃分，即求解點雲Q的包圍盒，並對該包圍盒進行細分，對包含於不同體素的源點雲分別構建高斯模型。該演算法最大的優勢是迭代過程中不需要求解最近鄰匹配點，其計算複雜度較低。其中體素的劃分方式與點雲配準的精度和效率相關，可利用迴環控制點雲配準精度，主要應用於機器人的實時Simultaneous Localization And Mapping（SLAM）環節。Jian等提出利用混合高斯模型替代單一的高斯模型。為了提高配準模型的魯棒性，體素高斯模型被分別進行加權計算，其中多尺度的點雲配準方法應用較為廣泛，如NDT、EM-ICP等。上述基於概率模型的點雲配准算法只需在每次迭代中求解雅可比矩陣，計算複雜度大大降低，且Magnusson等指出NDT演算法較ICP演算法能更好地避免點雲初始位置對配準結果的影響。
針對點雲配準的精度問題，部分學者提出了點到面的點雲配准算法，利用曲線、曲面擬合求解出源點雲的顯、隱式表達，並利用法向量求解每次迭代中的對應點對，如下圖所示

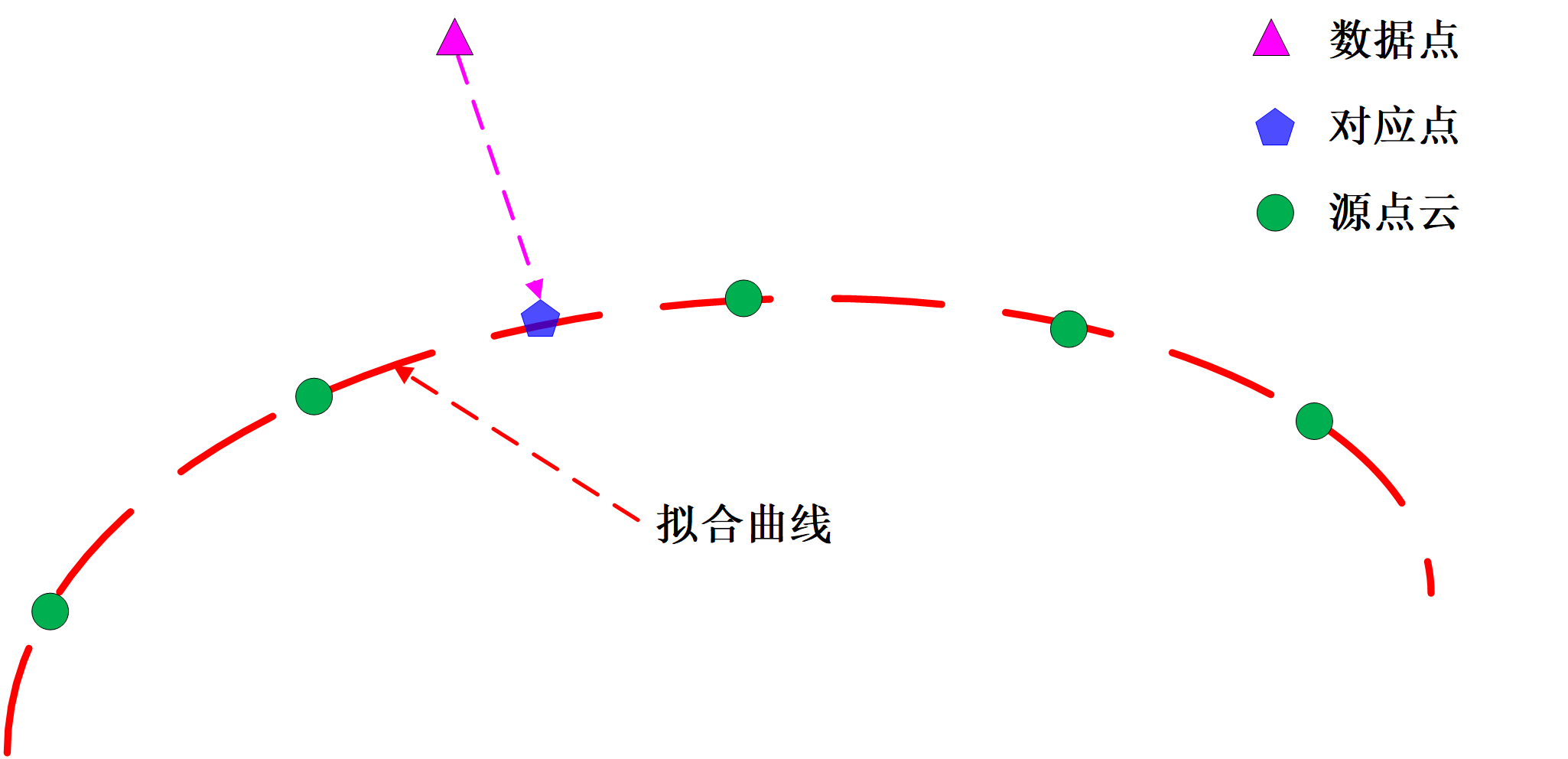
Liu等提出利用動曲面構建源點雲的拓撲外形實現點雲配準，主要應用於簡單形狀組合而成的零件點雲配準問題，如圓錐、圓柱、旋轉掃掠螺旋曲面等。為了解決複雜外形點雲的配準問題，學者提出了魯棒性更強的曲面擬合方法，如B樣條模型、八叉樹結點等。該類配准算法的實用性更強且應用範圍更廣。在此基礎上，張等分析了移動最小二乘法在曲面擬合應用中的發展及其優越性，並提出該方法能實現精確的點雲配準且對噪聲具有良好的魯棒性。但是此類演算法其需要預先設定較好的引數，如分支數、權值等。
相較之下，迭代最近點的點雲配准算法的魯棒性更強，因其不需設定冗餘的優化引數，但其它演算法則在提高效率和精度方面更具優勢。上述區域性演算法及其變種廣泛應用於解決點雲配準問題，且可有效避免噪聲和離群值對配準結果的影響。但是，此類配准算法受限於點雲初始位置，容易陷入區域性最優。區別於此類具有魯棒性的區域性配准算法，學者針對點雲初始配準位置的優化問題提出了一系列全域性優化的配准算法。

--全域性的3D點雲配准算法--

Silva等將點雲配準問題轉換為多變數的非凸優化問題，並結合遺傳演算法求解出全域性優化的變換矩陣，能有效避免點雲初始位置對配準結果的影響。其他應用於點雲全域性配準的智慧演算法還包括粒子群演算法、模擬退火等。然而，此類啟發式演算法需多次呼叫配準模型進行優化求解，在處理大規模點雲配準問題時效率較低，且其全域性解並未有嚴格的證明。為了提高點雲配準效率，部分學者提出通過構造幾何不變數匹配對應點對（理論上三組匹配點對就可求解出點雲配準的變換矩陣），該類方法同樣不受點雲初始位置影響，且計算複雜度更低。Wyngaerd等通過曲率特徵求解對應點對，實現點雲全域性配準；Gelfand等則通過構造積分體積特徵計算匹配點對求解變換矩陣；Rusu等提出構造點特徵直方圖作為區域性描述符。RANSAC方法被直接應用於點雲配準，但受限於其配準效率，一開始主要應用於解決二維的點雲配準問題。隨後，Aiger等利用4點法構造幾何特徵進而提取稀疏的匹配點對，使得RANSAC方法能有效地應用於三維點雲配準。當點雲的特徵不變數較為明顯時，基於幾何不變數的點雲配準方法可以作為效能優異的演算法使用。
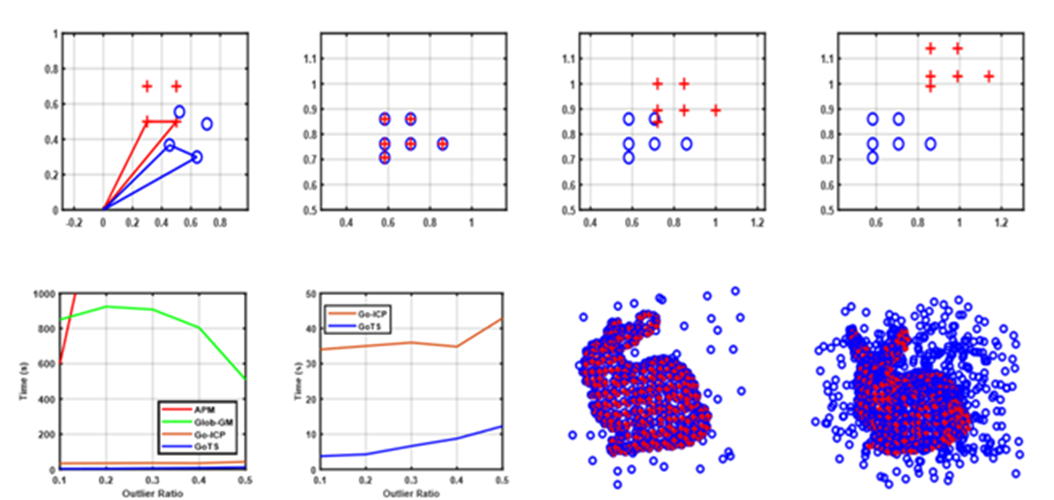
Yang等基於 範數配準模型首次推匯出了關於六維變換域的上下界函式，並利用分支定界演算法提出了全域性優化的Go-ICP演算法，且該演算法有效地證明了所求解變換矩陣的全域性最優性。但是，Go-ICP演算法需結合DT演算法才可能高效地實現點雲配準，而DT演算法的初始化較為耗時。Lian等提出了更為高效的AMP演算法進行點雲全域性優化配準，但其主要適用於影象處理領域。為了提高點雲配準效率，Chin等提出了Glob-GM-ML演算法將六維的點雲配準問題分解為兩個獨立的三維平移、旋轉問題，該演算法通過構建特徵不變數求解平移引數並認為其在配準問題中是先驗的，即六維的點雲配準問題有效地轉化為關於旋轉的三維非凸優化問題。該方法利用解耦的思想高效地實現點雲全域性優化配準，是近些年研究的熱點之一，Liu和Li等基於旋轉不變數並利用分支定界方法求解出全域性優化的平移引數，進而實現高效的點雲全域性優化配準。

為了解決構造旋轉不變數是的超引數設定問題，Yang等利用多項式時間提出了TEASER演算法對解決具有極高離群值的點雲全域性配準問題具有良好的魯棒性。區別於應用於CPU常規硬體的全域性點雲配准算法，GOGMA演算法等基於混合高斯模型構建了適用於GPU框架的高效點雲全域性優化配准算法，即在全域性優化過程中可利用GPU框架實現平行計算，提高加速點雲全域性優化配準效率。

參考文獻

[1] Besl P J, Mckay N D. A Method for Registration of 3-D Shapes[M]. 1992: 239-256.
[2] Yang J, Li H, Campbell D, et al. Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2016, 38(11): 2241-2254.
[3] Fitzgibbon A W. Robust registration of 2D and 3D point sets[J]. Image & Vision Computing, 2001, 21(13): 1145-1153.
[4] Moré J J. The Levenberg-Marquardt algorithm: Implementation and theory[J]. Lecture Notes in Mathematics, 1978, 630: 105-116.
[5] Chetverikov D, Svirko D, Stepanov D, et al. The Trimmed Iterative Closest Point algorithm[J], 2002.
[6] Bouaziz S, Tagliasacchi A, Pauly M. Sparse iterative closest point[C]. Eleventh Eurographics/acmsiggraph Symposium on Geometry Processing, 2013.
[7] Mavridis P, Andreadis A, Papaioannou G. Efficient Sparse ICP[J]. Computer Aided Geometric Design, 2015, 35-36(C): 16-26.
[8] Li W, Song P. A modified ICP algorithm based on dynamic adjustment factor for registration of point cloud and CAD model[J]. Pattern Recognition Letters, 2015, 65(65): 88-94.
[9] Zhu J, Jin C, Jiang Z, et al. Robust point cloud registration based on both hard and soft assignments[J]. Optics & Laser Technology, 2019, 110: 202-208.
[10] Biber P, Strasser W. The normal distributions transform: a new approach to laser scan matching[J]. Proc.of IEEE/RSJ Intl Conf.on Intelligent Robots & Systems, 2003, 3: 2743-2748 vol.3.
[11] Engel J, Schöps T, Cremers D. LSD-SLAM: Large-Scale Direct Monocular SLAM[M]. 2014.
[12] Jian B, Vemuri B C. A Robust Algorithm for Point Set Registration Using Mixture of Gaussians[C]. Tenth IEEE International Conference on Computer Vision, 2005.
[13] Granger S, Pennec X. Multi-scale EM-ICP: A Fast and Robust Approach for Surface Registration[C]. Computer Vision - ECCV 2002, 7th European Conference on Computer Vision, Copenhagen, Denmark, May 28-31, 2002, Proceedings, Part IV, 2002.
[14] Magnusson M, Nuchter A, Lorken C, et al. Evaluation of 3D Registration Reliability and Speed - A Comparison of ICP and NDT[C]. IEEE International Conference on Robotics & Automation, 2009.
[15] Liua Y. Constrained 3D shape reconstruction using a combination of surface fitting and registration[J]. Computer-Aided Design, 2006, 38(6): 572-583.
[16] Huang Y, Qian X, Chen S. Multi-sensor calibration through iterative registration and fusion[J]. Computer-Aided Design, 2009, 41(4): 240-255.
[17] Huang Q-X, Adams B, Wand M. Bayesian Surface Reconstruction via Iterative Scan Alignment to an Optimized Prototype[J]. Proc Eurographics Symposium on Geometry Processing, 2007, (2007): 213-223.
[18] Levin, David. The approximation power of moving least-squares [J]. Mathematics of Computation, 67(224): 1517-1532.
[19] Zuppa C. Good quality point sets and error estimates for moving least square approximations[J]. Applied Numerical Mathematics, 47(3-4): 575-585.
[20] Dey T K, Sun J. . An Adaptive MLS Surface for Reconstruction with Guarantees[C]. Third Eurographics Symposium on Geometry Processing, Vienna, Austria, July 4-6, 2005, 2005.
[21] Ahn S J, Yoo J, Lee B G, et al. 3D Surface Reconstruction from Scattered Data Using Moving Least Square Method[C]. Image Analysis and Processing - ICIAP 2005, 13th International Conference, Cagliari, Italy, September 6-8, 2005, Proceedings, 2005.
[22] Silva L, Bellon O R P, Boyer K L. Multiview range image registration using the surface interpenetration measure ☆[J]. Image & Vision Computing, 2007, 25(1): 114-125.
[23] Sandhu R, Dambreville S, Tannenbaum A. Point set registration via particle filtering and stochastic dynamics[J]. IEEE transactions on pattern analysis and machine intelligence, 2010, 32(8): 1459-1473. [24] Wachowiak M P, Smolíková R, Zheng Y, et al. An Approach to Multimodal Biomedical Image Registration Utilizing Particle Swarm Optimization[J]. Evolutionary Computation IEEE Transactions on, 2004, 8(3): 289-301.
[25] Papazov C, Burschka D. Stochastic global optimization for robust point set registration[J]. Computer Vision & Image Understanding, 2011, 115(12): 1598-1609.
[26] Wyngaerd J V, Gool L V. Automatic Crude Patch Registration: Toward Automatic 3D Model Building[J]. Computer Vision & Image Understanding, 2002, 87(1–3): 8-26.
[27] Desbrun M, Pottmann H, Gelfand N, et al. Robust Global Registration[J]. Proceedings of Eurographics Symposium on Geometry Processing, 2008: 197.
[28] Rusu R B, Blodow N, Beetz M. Fast Point Feature Histograms (FPFH) for 3D registration[C]. Robotics and Automation, 2009. ICRA '09. IEEE International Conference on, 2009.
[29] Fischler M A, Bolles R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography[M]. ACM, 1981: 726-740.
[30] Irani S, Raghavan P. Combinatorial and experimental results for randomized point matching algorithms[C], 1996.
[31] Aiger D, Mitra N J, Cohenor D. 4-points congruent sets for robust pairwise surface registration[J]. Acm Transactions on Graphics, 2011, 27(3): 1-10.
[32] Lian W, Zhang L, Yang M H. An Efficient Globally Optimal Algorithm for Asymmetric Point Matching[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2017, 39(7): 1281-1293.
[33] Chin T J, Suter D. Fast Rotation Search with Stereographic Projections for 3D Registration[C]. IEEE Conference on Computer Vision and Pattern Recognition, 2014: 3930-3937.
[34] Liu Y, Wang C, Song Z, et al. Efficient Global Point Cloud Registration by Matching Rotation Invariant Features Through Translation Search: 15th European Conference, Munich, Germany, September 8–14, 2018, Proceedings, Part XII[M]. 2018.
[35] Li X, Liu Y, Wang Y, et al. Fast and Globally Optimal Rigid Registration of 3D Point Sets by Transformation Decomposition[J], 2018.
[36] Yang H, Carlone L. A Polynomial-time Solution for Robust Registration with Extreme Outlier Rates[J].
[37] Campbell D, Petersson L. GOGMA: Globally-Optimal Gaussian Mixture Alignment[J].
[38] Straub J, Campbell T, How J P, et al. Efficient Global Point Cloud Alignment using Bayesian Nonparametric Mixtures[J].

更多精彩內容請關注訂閱號優化與演算法和加入QQ討論群1032493483獲取更多資料

原文連結：https://mp.weixin.qq.com/s?__biz=Mzg5MjI1NTAzOA==&mid=2247484207&idx=1&sn=7a1e1e4885ea86bdab8267246f34ef38&chksm=cfc1ad7ef8b6246864034b56d4a18b814876b55673f4fa934d198820f3d0ae39792e9d62594e&token=1727301402&lang=zh_CN