每一個遊戲可以呈現炫麗效果的背後，需要進行一系列的複雜計算，同時也伴隨著各種各樣的頂點空間變換。渲染遊戲的過程可以理解成是把一個個頂點經過層層處理最終轉化到螢幕上的過程，本文就旨在說明，頂點是經過了哪些座標空間後，最終被畫在了我們的螢幕上。 ## 空間變換的原理 首先，我們來看一個簡單的問題：當給定一個座標空間以及其中一點(a, b, c)時，我們是如何知道該點的位置的呢？ 1. 從座標空間的原點開始 2. 向x軸方向移動a個單位 3. 向y軸方向移動b個單位 4. 向z軸方向移動c個單位 座標空間的變換就蘊含在上面的4個步驟中。現在，我們已知座標空間C的3個座標軸在座標空間P下的表示X_c, Y_c, Z_c，以及其原點位置O_c。當給定座標空間C中的一點A_c = (a, b, c)，我們同樣可以依照上面4個步驟來確定其在座標空間P下的位置A_p 1. 從座標空間的原點開始，即 O_c 2. 向x軸方向移動a個單位，即 O_c + aX_c 3. 向y軸方向移動b個單位，即 O_c + aX_c + bY_c 4. 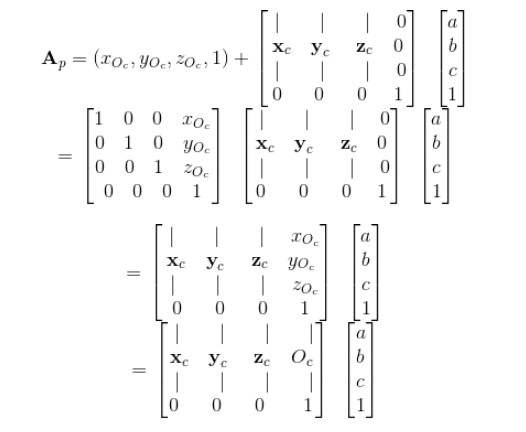向z軸方向移動c個單位，即 O_c + aX_c + bY_c + cZ_c 對得到的表示式做如下變換，其中“|”符號表示按列展開  繼續對其中的加法表示式做變換，即擴充套件到齊次座標空間做平移變換  現在，我們得到了座標空間C到座標空間P的變換矩陣M_c->p  可以看出M_c->p實際上是通過座標空間C在座標空間P中的原點和座標軸的矢量表示構建出來的：把3個座標軸依次放入矩陣的前3列，把原點向量放到最後一列，再用0和1填充最後一行即可。 我們可以利用反向思維，從這個變換矩陣中提取出座標空間C的原點和座標軸在座標空間P的表示。例如，當我們已知從模型空間到世界空間的4×4變換矩陣，我們可以提取出它的第一列，再進行歸一化（為了消除縮放的影響）來得到模型空間的x軸在世界空間下的單位矢量表示。同樣的方法可以提取y軸和z軸。 當對方向向量進行座標空間變換時，由於向量是沒有位置的，因此座標空間的原點變換是可以忽略的。那麼對方向向量的座標空間變換就可以使用3×3的矩陣來表示，即  在Shader中，我們常常看到擷取變換矩陣的前3行前3列來對法線方向，光照方向進行空間變化，這正是原因所在。 一旦求出來M_c->p，M_p->c就可以通過求逆矩陣的方式求出來，因為從座標空間C變換到座標空間P與從座標空間P變換到座標空間C是互逆的兩個過程。當M_c->p是一個**正交矩陣**時，M_c->p的逆矩陣就等於它的轉置矩陣，即  此時，我們還可以通過M_c->p反推出座標空間P的座標軸在座標空間C中的表示X_p, Y_p, Z_p，這些座標軸對應的就是M_c->p的每一行。 ## 模型空間 模型空間，是和某個模型或者說是物件有關的，模型空間也被稱為物件空間或區域性空間。 每個模型都有自己獨立的座標空間，當它移動或旋轉的時候，模型空間也會跟著移動和旋轉。 Unity在模型空間中使用的是左手座標系，因此在模型空間中，+x軸，+y軸，+z軸分別對應的是模型的右，上，前向。 模型空間的原點和座標軸通常是由美術人員在建模軟體裡確定好的。當匯入到Unity中後，我們可以在頂點著色器中訪問到模型的頂點資訊，其中就包含了每個頂點的座標。這些座標都是相對於模型空間中的原點（通常位於模型的重心）定義的。 ## 世界空間 世界空間是一個特殊的座標系，因為它建立了我們所關心的最大空間，即整個遊戲空間 在Unity中，世界空間同樣使用了左手座標系。它的x軸，y軸，z軸是固定不變的。 頂點變換的第一步，就是將頂點座標從模型空間轉換到世界空間中，這個變換通常叫做**模型變換** 在Unity中，我們可以通過Transform元件中的值得知模型做了哪些變換。這個值是根據Transform的父節點的模型座標空間中的原點定義的，如果這個Transform沒有任何父節點，那麼這個值就是相對於世界座標空間定義的。 要將模型空間中的一點轉換到其父空間中，需要獲取M_子->父，這個矩陣可以通過模型的Transform值得到。Transform中包含了旋轉，縮放和平移值，則M_子->父 = M_translation M_rotate M_scale。而從模型空間轉換到世界空間的變換矩陣M_{模型->世界}可以通過子空間到父空間變換矩陣，父空間到爺爺空間變換矩陣，連乘，直到世界空間為止得到。 ## 觀察空間 觀察空間也被稱為攝像機空間，可以認為是模型空間的一個特例，即攝像機的模型空間。 在Unity中，觀察空間使用的是右手座標系，即+x軸指向右方，+y軸指向上方，+z軸指向攝像機後方 頂點變換的第二步就是將頂點座標從世界空間變換到觀察空間中。這個變換通常叫做**觀察變換**。 從觀察空間到世界空間的變換矩陣我們同樣可以通過Transform中的值得到，再對該矩陣求逆得到從世界空間到觀察空間的變換矩陣。我們還可以使用另一種方法，對Transform元件中的值直接取反（做逆向變換），然後得到從世界空間到觀察空間的變換矩陣。注意，由於觀察空間使用的是右手座標系，因此還需要對變換矩陣的z分量進行取反操作。 ## 裁剪空間 頂點接下來要從觀察空間轉換到裁剪空間中，這個變換可以被稱為**投影變換**。這個用於變換的矩陣叫做**裁剪矩陣**或是**投影矩陣** 裁剪空間的目的是能夠方便地對渲染圖元進行裁剪：完全位於這塊空間內部的圖元將會被保留，完全位於這塊空間外部的圖元將會被剔除，與這塊空間邊界相交的圖元就會被裁剪。而這塊空間就是由視椎體來決定的。 視椎體有兩種型別，分別對應兩種投影型別：透視投影（下圖左）和正交投影（下圖右）。透視投影模擬了人眼看世界的方式，而正交投影則完全保留了物體的距離和角度。  投影矩陣雖然叫做投影矩陣，但並沒有真正進行投影，而是為投影做準備。目的是對x，y，z分量進行縮放，經過投影矩陣的縮放後，我們可以直接使用w分量作為範圍值，只有x，y，z分量都位於這個範圍內的頂點才認為是在裁剪空間內。並且w分量在真正的投影時也會用到。 透視投影和正交投影分別對應了不同的投影矩陣。還需要注意的是投影矩陣會改變空間的旋向性：空間從右手座標系變換到了左手座標系 ### 透視投影  其中FOV表示視椎體垂直方向的張開角度，而Near和Far分別控制了近裁剪平面和遠裁剪平面距離攝像機的遠近。這樣我們可以求出近裁剪平面的高度，如下所示。遠裁剪平面類似。  而根據攝像機的橫縱比資訊，我麼就可以得到近裁剪平面的寬度  一個頂點和透視投影的投影矩陣相乘後得到的結果如下  視椎體的變化如下所示  此時我們就可以按如下不等式來判斷一個變換後的頂點是否位於視椎體內  ### 正交投影  其中Size表示視椎體豎直方向上高度的一半，而Near和Far同樣分別控制了近裁剪平面和遠裁剪距離攝像機的遠近。則近裁剪平面的高度如下所示。遠裁剪平面類似。  近裁剪平面的高度同樣可以通過攝像機的縱橫比得到  一個頂點和正交投影的投影投影矩陣相乘後得到的結果如下  視椎體的變化如下所示  判斷一個變換後的頂點是否位於視椎體內使用的不等式和透視投影中的一樣，這種通用性也是為什麼要使用投影矩陣的原因之一。 ## 螢幕空間 當完成了所有的裁剪工作後，就需要進行真正的投影了，即把視椎體投影到螢幕空間中，這個過程可以被稱為**螢幕對映**。經過這一步變換，我們會得到真正的畫素位置，對應的2D座標，而不是虛擬的三維座標。這個過程可以理解成有兩步： 1. 進行標準**齊次除法**，也被稱為透視除法。就是把齊次座標系的x，y，z分量都除以w分量。在OpenGL中把這一步得到的座標叫做歸一化的裝置座標（NDC）。經過透視投影變換後的裁剪空間會變換到一個立方體內，而正交投影的裁剪空間本身就是一個立方體（它的w分量是1，齊次除法不會對它產生影響）。在Unity中這個立方體的x，y，z分量的範圍都是[-1, 1]，和OpenGL保持一致。  2. 經過齊次除法後，透視投影和正交投影的視椎體都變換到一個相同的立方體內。現在，我們可以根據變換後的x，y座標來對映輸出視窗對應的畫素座標。 在Unity中，螢幕空間左下角的畫素是(0, 0)，右上角的畫素座標是(pixelWidth, pixelHeight)。齊次除法和螢幕對映的過程可以使用下面的公式來表示 $$screen_x = \frac{clip_x * pixelWidth}{2 * clip_w} + \frac{pixelWidth}{2}$$ $$screen_y = \frac{clip_y * pixelHeight}{2 * clip_w} + \frac{pixelHeight}{2}$$ 在Unity中，從裁剪空間到螢幕空間的轉換是由底層幫我們完成的。我們的頂點著色器只需要把頂點轉換到裁剪空間即可（模型空間-世界空間-觀察空間-裁剪空間，對應的矩陣通常會串聯成一個MVP矩陣）。 ## 法線變換 最後，我們再來看一種特殊的變換：法線變換。在遊戲中，模型的一個頂點往往會攜帶額外的資訊，而頂點法線和切線就是其中的兩種資訊，切線和法線是互相垂直的。 由於切線是由兩個頂點之間的差值計算得到的，因此我們可以直接使用變換頂點的矩陣M_A->B來變換切線。但如果直接使用M_A->B來變換法線，得到的新法線可能就不會和切線垂直了。例如下圖所示.  那麼應該使用哪個矩陣來變換法線呢？我們可以通過數學約束條件推出這個矩陣。由於頂點法線N_A和切線T_A垂直，則T_AN_A = 0。給定變換矩陣M_A->B，我們已知T_B = M_A->BT_A。現在我們要找到一個矩陣G來變換法線N_A，使得變換後的法線仍然與切線垂直，即  通過一些推導可得  由於T_AN_A = 0，因此可得  即  這說明使用原變換矩陣的逆轉置矩陣來變換法線就可以得到正確的結果。 值得注意的是，如果矩陣M_A->B是正交矩陣，則我們可以直接使用原變換矩陣作為法線的變換矩陣。如果變換隻包含旋轉和統一縮放，我們可以利用統一縮放係數k來得到變換矩陣M_A->B的逆轉置矩陣，這樣可以避免計算逆矩陣的過程。  ## 視口空間 視口空間中的座標被稱為視口座標，就是把螢幕歸一化，這樣螢幕左下角就是(0, 0)，右上角就是(1, 1)。如果已知螢幕座標的話，我們只需要把x，y分量除以螢幕解析度即可得到視口座標。如果已知裁剪空間中的座標，可以通過以下公式得到視口座標 ![](https://img2020.cnblogs.com/blog/1673734/202003/1673734-20200322193444929-7012011