線上優化演算法 FTRL 的原理與實現
線上學習想要解決的問題
線上學習 ( \(\it{Online \;Learning}\) ) 代表了一系列機器學習演算法,特點是每來一個樣本就能訓練,能夠根據線上反饋資料,實時快速地進行模型調整,使得模型及時反映線上的變化,提高線上預測的準確率。相比之下,傳統的批處理方式需要一次性收集所有資料,新資料到來時重新訓練的代價也很大,因而更新週期較長,可擴充套件性不高。
一般對於線上學習來說,我們致力於解決兩個問題: 降低 regret 和提高 sparsity。其中 regret 的定義為:
\[\text{Regret} = \sum\limits_{t=1}^T \ell_t(\bold{w}_t) - \min_\bold{w}\sum\limits_{t=1}^T\ell_t(\bold{w}) \]其中 \(t\) 表示總共 \(T\) 輪中的第 \(t\) 輪迭代,\(\ell_t\) 表示損失函式,\(\bold{w}\) 表示要學習的引數。第二項 \(\min_\bold{w}\sum_{t=1}^T\ell_t(\bold{w})\) 表示得到了所有樣本後損失函式的最優解,因為線上學習一次只能根據少數幾個樣本更新引數,隨機性較大,所以需要一種穩健的優化方式,而 regret 字面意思是 “後悔度”,意即更新完不後悔。
在理論上可以證明,如果一個線上學習演算法可以保證其 regret 是 \(t\) 的次線性函式,則:
\[\lim_{t \to \infty}\frac{\text{Regret}(t)}{t} = 0 \]那麼隨著訓練樣本的增多,線上學習出來的模型無限接近於最優模型。而毫不意外的,FTRL 正是滿足這一特性。
另一方面,現實中對於 sparsity,也就是模型的稀疏性也很看中。上億的特徵並不鮮見,模型越複雜,需要的儲存、時間資源也隨之升高,而稀疏的模型會大大減少預測時的記憶體和複雜度。另外稀疏的模型相對可解釋性也較好,這也正是通常所說的 L1 正則化的優點。
後文主要考察 FTRL 是如何實現降低 regret 和提高 sparsity 這兩個目標的。
FTRL 原理
網上很多資料都是從 FTRL 的幾個前輩,FOBOS、RDA 等一步步講起,本篇就不繞那麼大的圈子了,直接從最基本的 OGD 開路到 FTRL 。OGD ( \(\it{online \;gradient \; descent}\) ) 是傳統梯度下降的 online 版本,引數更新公式為:
\(t\) 表示第 \(t\) 輪迭代,注意上式中的學習率 \(\eta_t\) 每輪都會變,一般設為 \(\eta_t = \frac{1}{\sqrt{t}}\)
OGD 在準確率上表現不錯,即 regret 低,但在上文的另一個考量因素 sparsity 上則表現不佳,即使加上了 L1 正則也很難使大量的引數變零。一個原因是浮點運算很難讓最後的引數出現絕對零值;另一個原因是不同於批處理模式,online 場景下每次 \(\bold {w}\) 的更新並不是沿著全域性梯度進行下降,而是沿著某個樣本的產生的梯度方向進行下降,整個尋優過程變得像是一個“隨機” 查詢的過程,這樣 online 最優化求解即使採用 L1 正則化的方式, 也很難產生稀疏解。正因為 OGD 存在這樣的問題,FTRL 才致力於在準確率不降低的前提下提高稀疏性。
相信大部分人對於 \((1.1)\) 式都不陌生,然而其實際等價於下式:
\[\bold{w}_{t+1} = \mathop{\text{argmin}}_\bold{w} \left(\bold{g}_t \cdot \bold{w} + \frac{1}{2\eta_t}||\bold{w} - \bold{w}_t||_2^2 \right) \tag{1.2} \]對 \((1.2)\) 式直接求導即可,\(\bold{g}_t + \frac{1}{\eta_t}(\bold{w} - \bold{w}_t) = 0 \;\;\implies\;\; \bold{w} = \bold{w}_t - \eta_t \bold{g}_t\) 。有了 \((1.2)\) 式的基礎後,後面 FTRL 的那些奇奇怪怪的變換就能明瞭了,目的無非也是降低 regret 和提高 sparsity 。
首先,為了降低 regret,FTRL 用 \(\bold{g}_{1:t}\) 代替 \(\bold{g}_t\) ,\(\bold{g}_{1:t}\) 為前 1 到 t 輪損失函式的累計梯度,即 \(\bold{g}_{1:t} = \sum_{s=1}^t \bold{g}_s = \sum_{s=1}^t \nabla \ell_s(\bold{w}_s)\) 。由於線上學習隨機性大的特點,累計梯度可避免由於某些維度樣本區域性抖動太大導致錯誤判斷。這是從 FTL ( \(\it{Follow \; the\; Leader}\) ) 那借鑑而來的,而 FTRL 的全稱為 \(\it{Follow \; the\; Regularized \;Leader}\) ,從名字上看其實就是在 FTL 的基礎上加上了正則化項,即 \((1.2)\) 式中的
\(||\bold{w} - \bold{w}_t||_2^2\) 項。這意味著每次更新時我們不希望新的 \(\bold{w}\) 離之前的 \(\bold{w}_t\) 太遠 (這也是有時其被稱為 FTRL-proximal 的原因),這同樣是為了降低 regret,線上學習噪音大,若一次更新錯得太遠後面難以收回來,沒法輕易“後悔”。
其次,為提高 sparsity ,最直接的方法就是無腦加 L1 正則。但這裡的問題是上文中 OGD 加了 L1 正則不能產生很好的稀疏性,那麼 FTRL 為什麼就能呢?這在後文的具體推導中會逐一顯現,耐心看下去就是。另外 FTRL 2013 年的工程論文中也加上了 L2 正則,所以綜合上述幾點,FTRL 的更新公式變為:
\[\bold{w}_{t+1} = \mathop{\text{argmin}}_{\bold{w}}\left(\bold{g}_{1:t} \cdot \bold{w} + \frac12 \sum\limits_{s=1}^t \sigma_s ||\bold{w} - \bold{w}_s||_2^2 + \lambda_1||\bold{w}||_1 + \frac12 \lambda_2||\bold{w}||_2^2\right) \tag{1.3} \]其中 \(\sigma_s = \frac{1}{\eta_s} - \frac{1}{\eta_{s-1}}\) ,則 \(\sigma_{1:t} = \sum_{s=1}^t \sigma_s = \frac{1}{\eta_s}\) ,主要是為了後面推導和實現方便而這麼設定,後文再述。
下面可以推導 FTRL 的演算法流程,將 \((1.3)\) 式中的 \(||\bold{w} - \bold{w}_s||_2^2\) 展開:
\[\bold{w}_{t+1} = \mathop{\text{argmin}}_{\bold{w}} \left\{ \left(\bold{g}_{1:t} - \sum\limits_{s=1}^t\sigma_s\bold{w}_s \right) \cdot \bold{w} + \lambda_1||\bold{w}||_1 + \frac12 \left(\lambda_2 + \sum\limits_{s=1}^t \sigma_s \right) \cdot ||\bold{w}||_2^2 + \frac12 \sum\limits_{s=1}^t \sigma_s||\bold{w}_s||_2^2 \right\} \tag{1.4} \]由於 \(\frac12 \sum\limits_{s=1}^t \sigma_s||\bold{w}_s||_2^2\) 相對於要優化的 \(\bold{w}\) 是一個常數可以消去,並令 \(\bold{z}_t = \bold{g}_{1:t} - \sum\limits_{s=1}^t \sigma_s\bold{w}_s\) ,於是 \((1.4)\) 式變為:
\[\bold{w}_{t+1} = \mathop{\text{argmin}}_{\bold{w}} \left\{ \bold{z}_t \cdot \bold{w} + \lambda_1||\bold{w}||_1 + \frac12 \left(\lambda_2 + \sum\limits_{s=1}^t \sigma_s \right) \cdot ||\bold{w}||_2^2 \right\} \tag{1.5} \]將特徵的各個維度拆開成獨立的標量最小化問題,\(i\) 為 第 \(i\) 個特徵:
\[w_{t+1,i} = \mathop{\text{argmin}}_{w_i \in \mathbb{R}} \left\{ z_{t,i} \, w + \lambda_1 |w_i| + \frac12 \left(\lambda_2 + \sum\limits_{s=1}^t \sigma_s \right) \cdot w_i^2 \right\} \tag{1.6} \]\((1.6)\) 式是一個無約束的非平滑引數優化問題,其中第二項 \(\lambda_1|w_i|\) 在 \(w_i = 0\) 處不可導,因而常用的方法是使用次導數 (詳見附錄1),這裡直接上結論: 定義 \(\phi \in \partial |w_i^*|\) 為 \(|w_i|\) 在 \(w_i^*\) 處的次導數,於是有:
\[\partial |w_i^*| = \begin{cases} \quad\quad\{1\} &\quad \text{if}\;\; w_i^* > 0 \\[1ex] -1 < \phi < 1 & \quad \text{if}\;\; w_i^* = 0 \\[1ex] \tag{1.7} \quad\;\;\{-1\} &\quad \text{if}\;\; w_i^* < 0 \end{cases} \]有了 \(|w_i|\) 的次導數定義後,對 \((1.6)\) 式求導並令其為零:
\[z_{t,i} + \lambda_1 \phi + \left(\lambda_2 + \sum\limits_{s=1}^t \sigma_s\right)\cdot w_i = 0 \tag{1.8} \]上式中 \(\lambda_1 > 0\, , \;\; \left(\lambda_2 + \sum_{s=1}^t \sigma_s \right) > 0\) ,下面對 \(z_{t,i}\) 的取值分類討論:
(1) \(|z_{t, i}| < \lambda_1\) ,那麼 \(w_i = 0\) 。因為若 \(w_i > 0\) ,根據 \((1.7)\) 式 \(\phi = 1\) ,則 \((1.8)\) 式左側 \(> 0\) ,該式不成立;同樣若 \(w_1 < 0\),則 \((1.8)\) 式左側 \(< 0\),不成立。
(2) \(z_{t, i} > \lambda_1\),則 \(\phi = -1 \implies w_i = -\frac{1}{\lambda_2 + \sum_{s=1}^t \sigma_s} (z_{t, i} - \lambda_1) < 0\) 。因為若 \(w_i > 0\),\(\phi = 1\),\((1.8)\) 式左側 \(> 0\),不成立;若 \(w_i = 0\),由 \((1.8)\) 式 \(\phi = -\frac{z_{t,i}}{\lambda_1} < -1\) ,與 \((1.7)\) 式矛盾。
(3) \(z_{t,i} < -\lambda_1\),則 \(\phi = 1 \implies w_i = -\frac{1}{\lambda_2 + \sum_{s=1}^t \sigma_s} (z_{t, i} + \lambda_1) > 0\) 。因為若 \(w_i < 0\),\(\phi = -1\),\((1.8)\) 式左側 $ < 0$,不成立;若 \(w_i = 0\),由 \((1.8)\) 式 \(\phi = -\frac{z_{t,i}}{\lambda_1} > 1\) ,與 \((1.7)\) 式矛盾。
綜合這幾類情況,由 $(1.8) $ 式得到 \(w_{t,i}\) 的更新公式:
\[w_{t+1,i} = \begin{cases} \qquad\qquad \large{0} & \text{if}\;\; |z_{t,i}| < \lambda_1 \\[2ex] -\frac{1}{\lambda_2 + \sum_{s=1}^t\sigma_s} \left(z_{t,i} - \text{sgn}(z_{t,i})\cdot\lambda_1 \right) & \text{otherwise} \tag{1.9} \end{cases} \]可以看到當 \(z_{t,i} = \left(g_{1:t, i} - \sum_{s=1}^t \sigma_s w_{s, i} \right) < \lambda_1\) 時,引數置為零,這就是 FTRL 稀疏性的由來。另外加入 L2 正則並沒有影響模型的稀疏性,從 \((1.9)\) 式看只是使得分母變大,進而 \(w_i\) 更趨於零了,這在直覺上是符合正則化本身的定義的。
觀察 \((1.9)\) 式還遺留一個問題,$\sigma $ 的值是什麼呢?這牽涉到 FTRL 的學習率設定。當然嚴格意義上的學習率是 \(\eta_t\) ,而 \(\sigma_t = \frac{1}{\eta_t} - \frac{1}{\eta_{t-1}}\) ,論文中這樣定義可能是為了推導和實現的方便。前文 \((1.1)\) 式中 OGD 使用的是一個全域性學習率 \(\eta_t = \frac{1}{\sqrt{t}}\) ,會隨著迭代輪數的增加而遞減,但該方法的問題是所有特徵維度都使用了一樣的學習率。
FTRL 採用的是 Per-Coordinate Learning Rate,即每個特徵採用不同的學習率,這種方法考慮了訓練樣本本身在不同特徵上分佈的不均勻性。如果一個特徵變化快,則對應的學習率也會下降得快,反之亦然。其實近年來隨著深度學習的流行這種操作已經是很常見了,常用的 AdaGrad、Adam 等梯度下降的變種都蘊含著這類思想。FTRL 中第 \(t\) 輪第 \(i\) 個特徵的學習率為:
\[\eta_{t, i} = \frac{\alpha}{\beta + \sqrt{\sum_{s=1}^t g_{s, i}^2}} \tag{1.10} \]這樣 \((1.9)\) 式中的 \(\sum_{s=1}^t \sigma_s\) 為:
\[\begin{align*} \sum\limits_{s=1}^t \sigma_s &= (\frac{1}{\eta_t} - \frac{1}{\eta_{t-1}}) + (\frac{1}{\eta_{t-1}} - \frac{1}{\eta_{t-2}}) + \cdots + (\frac{1}{\eta_1} - \frac{1}{\eta_0}) \\ &=\;\; \frac{1}{\eta_t} \;\;=\;\; \frac{\beta + \sqrt{\sum_{s=1}^tg_{s,i}^2}}{\alpha} \tag{1.11} \end{align*} \]其中 \(\alpha, \beta\) 為超引數,論文中建議 \(\beta\) 設為 1,而 \(\alpha\) 則根據情況選擇。\(g_{s,i}\) 為第 \(s\) 輪第 \(i\) 個特徵的偏導數,於是 \((1.9)\) 式變為:
\[w_{t+1,i} = \begin{cases} \qquad\qquad \large{0} & \quad\text{if}\;\; |z_{t,i}| < \lambda_1 \\[2ex] - \left(\lambda_2 + \frac{\beta + \sqrt{\sum_{s=1}^t g_{s,i}^2}}{\alpha} \right)^{-1} \left(z_{t,i} - \text{sgn}(z_{t,i})\cdot\lambda_1 \right) & \quad \text{otherwise} \tag{1.12} \end{cases} \]綜合 \((1.10)\) 式和 \((1.12)\) 式可以看出,學習率 \(\eta_{t,i}\) 越大,則引數 \(w\) 更新幅度越大,這與學習率的直覺定義相符。
FTRL 實現
完整程式碼見 ( https://github.com/massquantity/Ftrl-LR ) ,實現了多執行緒版本 FTRL 訓練 Logistic Regression 。
對於演算法的實現來說,首先需要得到完整的演算法流程。仔細審視 \((1.12)\) 式,要在 \(t + 1\) 輪更新 \(w_{t+1, i}\) 需要哪些值? 需要 \(\{ \;z_{t,i}, \,g_{t,i}, \,\alpha, \,\beta, \,\lambda_1, \,\lambda_2 \; \}\) ,後四個為預先指定的超引數,對於 \(z_{t,i}\) ,注意其定義有可以累加的特性 :
\[\begin{aligned} z_{t,i} &= g_{1:t, i} - \sum\limits_{s=1}^t \sigma_{s, i} w_{s,i} \\ &= \sum\limits_{s=1}^t g_{s,i} - \sum\limits_{s=1}^t \sigma_{s, i} w_{s,i} \\ &= z_{t-1,i} + g_{t,i} - \sigma_{t,i}w_{t,i} \\[1ex] &= z_{t-1,i} + g_{t,i} - \left(\frac{1}{\eta_{t,i}} - \frac{1}{\eta_{t-1, i}} \right) w_{t,i} \\[1ex] &= z_{t-1,i} + g_{t,i} - \frac{\sqrt{\sum_{s=1}^t g_{s,i}^2} - \sqrt{\sum_{s=1}^{t-1} g_{s,i}^2}}{\alpha} w_{t,i} \end{aligned} \]所以我們只需儲存上一輪迭代得到的三個量 : \(z_{t-1,i}, \, w_{t,i}, \sqrt{\sum_{s=1}^t g_{s,i}^2}\) ,並在本輪迭代中計算 \(g_{t,i}\) ,就能不斷更新引數了。\(g_{t,i}\) 為損失函式對第 \(i\) 個特徵的偏導數,\(\text{Logistic Regression}\) 的損失函式是 \(\text{Log Loss}\),這裡直接給出結論,具體推導見附錄 2:
\[g_{t,i} = y_t (S(y_t f(\bold{x}_t)) - 1) x_i = y_t \left(\frac{1}{1 + e^{- y_t f(\bold{x}_t)}} - 1 \right) x_i \tag{2.1} \]其中 \(S(\cdot)\) 為 Sigmoid函式,\(x_i\) 為第 \(i\) 個特徵值, \(y \in \{-1, + 1\}\) 為標籤,\(f(\bold{x}_t) = \sum_{i=1}^I w_ix_i\) 。下面就可以給出完整的演算法流程了,其中為方便表示定義了 \(n_i = \sqrt{\sum_{s=1}^t g_{s,i}^2}\) :
輸入: 引數 \(\alpha, \,\beta, \,\lambda_1, \,\lambda_2\)
初始化: \(\bold{z}_0 = \bold{0}, \; \bold{n}_0 = \bold{0}\)
$\text{for t = 1 to T} : $
\(\qquad\) 收到一個樣本 \(\{\bold{x}_t, y_t\}\) ,\(y_t \in \{-1, + 1\}\) 。令 \(I\) 為所有不為零的特徵集合,即 \(I = \{i \,|\, x_i \neq 0\}\)
\(\qquad\) \(\text{for} \;\;i \in I\) 更新 \(w_{t,i}\) :
\[w_{t,i} = \begin{cases} \qquad\qquad \large{0} & \quad\text{if}\;\; |z_{i}| < \lambda_1 \\[2ex] - \left(\lambda_2 + \frac{\beta + \sqrt{n_i}}{\alpha} \right)^{-1} \left(z_{i} - \text{sgn}(z_{i})\cdot\lambda_1 \right) & \quad \text{otherwise} \end{cases} \] \(\qquad\) 使用更新後的 \(\bold{w}_t\) 計算 \(f(\bold{x}_t) = \bold{w}_t \cdot \bold{x}_t\)
\(\qquad\) \(\text{for all} \; i \in I :\)
\(\qquad\qquad\) \(g_i = y_t (S(y_t f(\bold{x}_t)) - 1) x_i\)
\(\qquad\qquad\) \(\sigma_i = \frac{\sqrt{n_i + g_i^2} - \sqrt{n_i}}{\alpha}\)
\(\qquad\qquad\) \(z_i \leftarrow z_i + g_i - \sigma_i w_{t,i}\)
\(\qquad\qquad\) \(n_i \leftarrow n_i + g_i^2\)
\(\qquad\) \(\text{end for}\)
\(\text{end for}\)
如上文所述,程式碼中使用了一個 ftrl_model_unit 類來儲存三個量 \(z_{i}, \, w_{i}, n_i\) :
class ftrl_model_unit
{
public:
double wi;
double w_ni;
double w_zi;
ftrl_model_unit()
{
wi = 0.0;
w_ni = 0.0;
w_zi = 0.0;
}
ftrl_model_unit(double mean, double stddev)
{
wi = utils::gaussian(mean, stddev);
w_ni = 0.0;
w_zi = 0.0;
}
}
更新引數的核心步驟為:
void ftrl_trainer::train(int y, const vector<pair<string, double> > &x)
{
ftrl_model_unit *thetaBias = pModel->getOrInitModelUnitBias();
vector<ftrl_model_unit *> theta(x.size(), nullptr);
int xLen = x.size();
for (int i = 0; i < xLen; ++i) {
const string &index = x[i].first;
theta[i] = pModel->getOrInitModelUnit(index); // 獲取相應的 ftrl_model_unit
}
for (int i = 0; i <= xLen; ++i) {
ftrl_model_unit &mu = i < xLen ? *(theta[i]) : *thetaBias;
if (fabs(mu.w_zi) <= w_l1)
mu.wi = 0.0;
else {
mu.wi = (-1) *
(1 / (w_l2 + (w_beta + sqrt(mu.w_ni)) / w_alpha)) *
(mu.w_zi - utils::sgn(mu.w_zi) * w_l1); // 更新 wi
}
}
double bias = thetaBias->wi;
double p = pModel->forecast(x, bias, theta); // 計算 f(x)
double mult = y * (1 / (1 + exp(-p * y)) - 1);
for (int i = 0; i <= xLen; ++i) {
ftrl_model_unit &mu = i < xLen ? *(theta[i]) : *thetaBias;
double xi = i < xLen ? x[i].second : 1.0;
double w_gi = mult * xi; // 更新 gi
double w_si = 1 / w_alpha * (sqrt(mu.w_ni + w_gi * w_gi) - sqrt(mu.w_ni));
mu.w_zi += w_gi - w_si * mu.wi; // 更新 zi
mu.w_ni += w_gi * w_gi; // 更新 ni
}
}
Appendix 1: 次導數
\((1.7)\) 式中使用了 \(f(x) = |x|\) 的次導數,這裡做一下具體推導。首先次導數的定義 —— 凸函式 \(f: \text{I} \rightarrow \mathbb{R}\) 在開區間 \(\text{I}\) 內的點 \(x_0\) 的次導數 \(c\) 滿足:
\[f(x) - f(x_0) \geq c(x - x_0) \]其物理含義是通過 \(x_0\) 下方的直線的斜率,如下圖,\(f(x)\) 在 \(x_0\) 處不可導,則經過 \(x_0\) 畫一條紅線,總是位於 \(f(x)\) 下方,其斜率就是次導數 \(c\) 。可以看出很多時候次導數並不唯一。
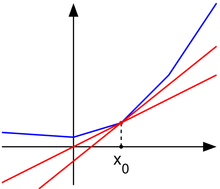
對於 \(f(x) = |x|\) 來說,\(x < 0\) 時,次導數為單元素集合 \(\{-1\}\) ,\(x > 0\) 時為 \(\{1\}\) 。而在 \(x = 0\) 處則不連續,根據次導數的定義,\(f(x) - f(0) \geqslant c\,(x - 0), \; f(x) \geqslant c\,x\) ,則滿足該式的 \(c \in [-1, 1]\) ,因而 \(f(x) = |x|\) 的次導數為 (如下圖所示):
\[\partial f(x) = \begin{cases} &\;\;\{1\} &\text{if}\;\; x > 0 \\[1ex] &[-1,1] & \text{if}\;\; x = 0 \\[1ex] &\;\{-1\} &\text{if}\;\; x < 0 \end{cases} \]
Appendix 2: $\text{Log Loss} $
FTRL 的演算法流程中每一輪更新都要計算損失函式對每個特徵分量的偏導數, 論文 中寫的是使用梯度,但實際上是梯度的一個分量,即偏導數,這裡就不作區分了。\(\text{Log Loss}\) 即 \(\text{Logistic Loss}\) ,其具體由來可參閱前文 《常見迴歸和分類損失函式比較》。僅考慮一個特徵的引數 \(w_i\) ,\(y \in \{-1, + 1\}\) 為標籤,$\text{Log Loss} $ 的形式為:
\[\mathcal{L}(y, \bold{w}) = \text{log}(1 + e^{-y\,f(\bold{x})}) = \text{log}(1 + e^{-y\,\sum_{i=1}^Iw_ix_i}) \tag{3.1} \]其中 \(f(\bold{x}_t) = \sum_{i=1}^I w_ix_i\) ,對 \(w_i\) 的偏導數為:
\[\begin{align*} \frac{\partial \mathcal{L}}{\partial w_i} &= \frac{e^{-y\,f(\bold{x})}}{1 + e^{-y\,f(\bold{x})}} (-yx_i) \\[1ex] &= y\left(\frac{1}{1 + e^{-yf(\bold{x})}} - 1 \right)x_i \\[1ex] &= y(S(yf(\bold{x})) - 1)x_i \end{align*} \]FTRL 論文 中採用的標籤形式是 \(y \in \{0,1\}\) ,因而損失函式的形式稍有不同:
\[\mathcal{L}(y, \bold{w}) = -y \, \text{log} \,p(\bold{w}^T\bold{x}) - (1-y) \, \text{log}(1-p(\bold{w}^T\bold{x})) \tag{3.2} \]其中 \(p(\bold{w}^T\bold{x}) = \frac{1}{1 + e^{- \bold{w}^T \bold{x}}}\) 為 Sigmoid 函式,其導數為:
\[p'(z) = - \frac{-e^{-z}}{(1 + e^{-z})^2} = \frac{1}{1 + e^{-z}} \cdot \frac{e^{-z}}{1 + e^{-z}}= p(z)(1 - p(z)) \tag{3.3} \]因而利用這個性質我們可以求出 \((3.2)\) 式關於 \(w_i\) 的偏導數:
\[\begin{align*} \frac{\partial{\mathcal{L}}}{\partial w_i} &= \left(-y \frac{1}{p(\bold{w}^T\bold{x})} + (1-y)\frac{1}{1 - p(\bold{w}^T\bold{x})} \right) \frac{\partial p(\bold{w}^T \bold{x})}{\partial w_i} \\[1ex] &= \left(-y \frac{1}{p(\bold{w}^T\bold{x})} + (1-y)\frac{1}{1 - p(\bold{w}^T\bold{x})} \right)p(\bold{w}^T\bold{x}) (1 - p(\bold{w}^T\bold{x})) x_i \qquad\text{利用(3.3)式} \\[1ex] &= \left(-y(1 - p(\bold{w}^T\bold{x}) + (1-y)p(\bold{w}^T\bold{x})\right) x_i \\[1ex] &= (p(\bold{w}^T\bold{x}) - y) x_i \end{align*} \]