python資料統計分析
1. 常用函式庫
scipy包中的stats模組和statsmodels包是python常用的資料分析工具,scipy.stats以前有一個models子模組,後來被移除了。這個模組被重寫併成為了現在獨立的statsmodels包。
scipy的stats包含一些比較基本的工具,比如:t檢驗,正態性檢驗,卡方檢驗之類,statsmodels提供了更為系統的統計模型,包括線性模型,時序分析,還包含資料集,做圖工具等等。
2. 小樣本資料的正態性檢驗
(1) 用途
夏皮羅維爾克檢驗法 (Shapiro-Wilk) 用於檢驗引數提供的一組小樣本資料線是否符合正態分佈,統計量越大則表示資料越符合正態分佈,但是在非正態分佈的小樣本資料中也經常會出現較大的W值。需要查表來估計其概率。由於原假設是其符合正態分佈,所以當P值小於指定顯著水平時表示其不符合正態分佈。
正態性檢驗是資料分析的第一步,資料是否符合正態性決定了後續使用不同的分析和預測方法,當資料不符合正態性分佈時,我們可以通過不同的轉換方法把非正太態資料轉換成正態分佈後再使用相應的統計方法進行下一步操作。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) x = stats.norm.rvs(loc=5, scale=10, size=80) # loc為均值,scale為方差 print(stats.shapiro(x)) # 執行結果:(0.9654011726379395, 0.029035290703177452)
(3) 結果分析
返回結果 p-value=0.029035290703177452,比指定的顯著水平(一般為5%)小,則拒絕假設:x不服從正態分佈。
3. 檢驗樣本是否服務某一分佈
(1) 用途
科爾莫戈羅夫檢驗(Kolmogorov-Smirnov test),檢驗樣本資料是否服從某一分佈,僅適用於連續分佈的檢驗。下例中用它檢驗正態分佈。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) x = stats.norm.rvs(loc=0, scale=1, size=300) print(stats.kstest(x,'norm')) # 執行結果:KstestResult(statistic=0.0315638260778347, pvalue=0.9260909172362317)
(3) 結果分析
生成300個服從N(0,1)標準正態分佈的隨機數,在使用k-s檢驗該資料是否服從正態分佈,提出假設:x從正態分佈。最終返回的結果,p-value=0.9260909172362317,比指定的顯著水平(一般為5%)大,則我們不能拒絕假設:x服從正態分佈。這並不是說x服從正態分佈一定是正確的,而是說沒有充分的證據證明x不服從正態分佈。因此我們的假設被接受,認為x服從正態分佈。如果p-value小於我們指定的顯著性水平,則我們可以肯定的拒絕提出的假設,認為x肯定不服從正態分佈,這個拒絕是絕對正確的。
4.方差齊性檢驗
(1) 用途
方差反映了一組資料與其平均值的偏離程度,方差齊性檢驗用以檢驗兩組或多組資料與其均值偏離程度是否存在差異,也是很多檢驗和演算法的先決條件。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) rvs1 = stats.norm.rvs(loc=5,scale=10,size=500) rvs2 = stats.norm.rvs(loc=25,scale=9,size=500) print(stats.levene(rvs1, rvs2)) # 執行結果:LeveneResult(statistic=1.6939963163060798, pvalue=0.19337536323599344)
(3) 結果分析
返回結果 p-value=0.19337536323599344, 比指定的顯著水平(假設為5%)大,認為兩組資料具有方差齊性。
5. 圖形描述相關性
(1) 用途
最常用的兩變數相關性分析,是用作圖描述相關性,圖的橫軸是一個變數,縱軸是另一變數,畫散點圖,從圖中可以直觀地看到相關性的方向和強弱,線性正相關一般形成由左下到右上的圖形;負相關則是從左上到右下的圖形,還有一些非線性相關也能從圖中觀察到。
(2) 示例
import statsmodels.api as sm import matplotlib.pyplot as plt data = sm.datasets.ccard.load_pandas().data plt.scatter(data['INCOMESQ'], data['INCOME'])
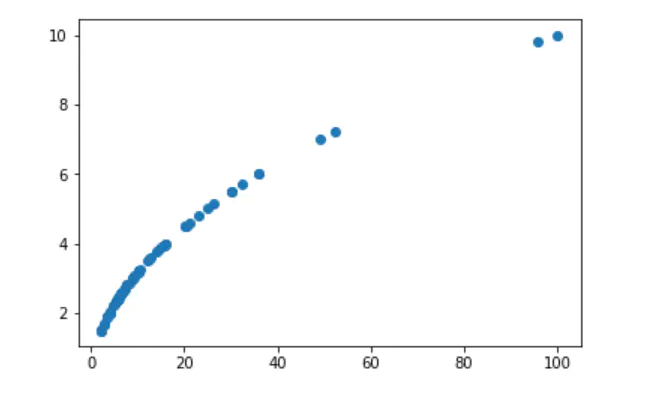
(3) 結果分析
從圖中可以看到明顯的正相關趨勢。
6. 正態資料的相關分析
(1) 用途
皮爾森相關係數(Pearson correlation coefficient)是反應倆變數之間線性相關程度的統計量,用它來分析正態分佈的兩個連續型變數之間的相關性。常用於分析自變數之間,以及自變數和因變數之間的相關性。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) a = np.random.normal(0,1,100) b = np.random.normal(2,2,100) print(stats.pearsonr(a, b)) # 執行結果:(-0.034173596625908326, 0.73571128614545933)
(3) 結果分析
返回結果的第一個值為相關係數表示線性相關程度,其取值範圍在[-1,1],絕對值越接近1,說明兩個變數的相關性越強,絕對值越接近0說明兩個變數的相關性越差。當兩個變數完全不相關時相關係數為0。第二個值為p-value,統計學上,一般當p-value<0.05時,可以認為兩變數存在相關性。
7. 非正態資料的相關分析
(1) 用途
斯皮爾曼等級相關係數(Spearman’s correlation coefficient for ranked data ),它主要用於評價順序變數間的線性相關關係,在計算過程中,只考慮變數值的順序(rank, 秩或稱等級),而不考慮變數值的大小。常用於計算型別變數的相關性。
(2) 示例
from scipy import stats import numpy as np print(stats.spearmanr([1,2,3,4,5], [5,6,7,8,7])) # 執行結果:SpearmanrResult(correlation=0.82078268166812329, pvalue=0.088587005313543812)
(3) 結果分析
返回結果的第一個值為相關係數表示線性相關程度,本例中correlation趨近於1表示正相關。第二個值為p-value,p-value越小,表示相關程度越顯著。
8. 單樣本T檢驗
(1) 用途
單樣本T檢驗,用於檢驗資料是否來自一致均值的總體,T檢驗主要是以均值為核心的檢驗。注意以下幾種T檢驗都是雙側T檢驗。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) rvs = stats.norm.rvs(loc=5, scale=10, size=(100,2)) print(stats.ttest_1samp(rvs, [1, 5])) # 執行結果:Ttest_1sampResult(statistic=array([ 5.12435977, 1.07927393]), pvalue=array([ 1.47820719e-06, 2.83088106e-01]))
(3) 結果分析
本例中生成了2列100行的陣列,ttest_1samp的第二個引數是分別對兩列估計的均值,p-value返回結果,第一列1.47820719e-06比指定的顯著水平(一般為5%)小,認為差異顯著,拒絕假設;第二列2.83088106e-01大於指定顯著水平,不能拒絕假設:服從正態分佈。
9. 兩獨立樣本T檢驗
(1) 用途
有於比較兩組資料是否來自於同一正態分佈的總體。注意:如果要比較的兩組資料不滿足方差齊性, 需要在ttest_ind()函式中新增引數equal_var = False。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) rvs1 = stats.norm.rvs(loc=5,scale=10,size=500) rvs2 = stats.norm.rvs(loc=6,scale=10,size=500) print(stats.ttest_ind(rvs1,rvs2)) # 執行結果:Ttest_indResult(statistic=-1.3022440006355476, pvalue=0.19313343989106416)
(3) 結果分析
返回結果的第一個值為統計量,第二個值為p-value,pvalue=0.19313343989106416,比指定的顯著水平(一般為5%)大,不能拒絕假設,兩組資料來自於同一總結,兩組資料之間無差異。
10. 配對樣本T檢驗
(1) 用途
配對樣本T檢驗可視為單樣本T檢驗的擴充套件,檢驗的物件由一群來自正態分佈獨立樣本更改為二群配對樣本觀測值之差。它常用於比較同一受試物件處理的前後差異,或者按照某一條件進行兩兩配對分別給與不同處理的受試物件之間是否存在差異。
(2) 示例
from scipy import stats import numpy as np np.random.seed(12345678) rvs1 = stats.norm.rvs(loc=5,scale=10,size=500) rvs2 = (stats.norm.rvs(loc=5,scale=10,size=500) + stats.norm.rvs(scale=0.2,size=500)) print(stats.ttest_rel(rvs1,rvs2)) 執行結果:Ttest_relResult(statistic=0.24101764965300979, pvalue=0.80964043445811551)
(3) 結果分析
返回結果的第一個值為統計量,第二個值為p-value,pvalue=0.80964043445811551,比指定的顯著水平(一般為5%)大,不能拒絕假設。
11. 單因素方差分析
(1) 用途
方差分析(Analysis of Variance,簡稱ANOVA),又稱F檢驗,用於兩個及兩個以上樣本均數差別的顯著性檢驗。方差分析主要是考慮各組之間的均數差別。
單因素方差分析(One-wayAnova),是檢驗由單一因素影響的多組樣本某因變數的均值是否有顯著差異。
當因變數Y是數值型,自變數X是分類值,通常的做法是按X的類別把例項成分幾組,分析Y值在X的不同分組中是否存在差異。
(2) 示例
from scipy import stats a = [47,56,46,56,48,48,57,56,45,57] # 分組1 b = [87,85,99,85,79,81,82,78,85,91] # 分組2 c = [29,31,36,27,29,30,29,36,36,33] # 分組3 print(stats.f_oneway(a,b,c)) # 執行結果:F_onewayResult(statistic=287.74898314933193, pvalue=6.2231520821576832e-19)
(3) 結果分析
返回結果的第一個值為統計量,它由組間差異除以組間差異得到,上例中組間差異很大,第二個返回值p-value=6.2231520821576832e-19小於邊界值(一般為0.05),拒絕原假設, 即認為以上三組資料存在統計學差異,並不能判斷是哪兩組之間存在差異 。只有兩組資料時,效果同 stats.levene 一樣。
12. 多因素方差分析
(1) 用途
當有兩個或者兩個以上自變數對因變數產生影響時,可以用多因素方差分析的方法來進行分析。它不僅要考慮每個因素的主效應,還要考慮因素之間的互動效應。
(2) 示例
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
import pandas as pd
X1 = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2]
X2 = [1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2]
Y = [76,78,76,76,76,74,74,76,76,55,65,90,65,90,65,90,90,79,70,90, 88,76,76,76,56,76,76,98,88,78,65,67,67,87,78,56,54,56,54,56]
data = {'T':X1, 'G':X2, 'L':Y}
df = pd.DataFrame(data)
formula = 'L~T+G+T:G' # 公式
model = ols(formula,df).fit()
print(anova_lm(model))
'''
執行結果:
df sum_sq mean_sq F PR(>F)
T 1.0 265.225 265.225000 2.444407 0.126693
G 1.0 207.025 207.025000 1.908016 0.175698
T:G 1.0 1050.625 1050.625000 9.682932 0.003631
Residual 36.0 3906.100 108.502778 NaN NaN
'''
(3) 結果分析
上述程式定義了公式,公式中,"~"用於隔離因變數和自變數,”+“用於分隔各個自變數, ":"表示兩個自變數互動影響。從返回結果的P值可以看出,X1和X2的值組間差異不大,而組合後的T:G的組間有明顯差異。
13. 卡方檢驗
(1) 用途
上面介紹的T檢驗是引數檢驗,卡方檢驗是一種非引數檢驗方法。相對來說,非引數檢驗對資料分佈的要求比較寬鬆,並且也不要求太大資料量。卡方檢驗是一種對計數資料的假設檢驗方法,主要是比較理論頻數和實際頻數的吻合程度。常用於特徵選擇,比如,檢驗男人和女人在是否患有高血壓上有無區別,如果有區別,則說明性別與是否患有高血壓有關,在後續分析時就需要把性別這個分類變數放入模型訓練。
基本資料有R行C列, 故通稱RC列聯表(contingency table), 簡稱RC表,它是觀測資料按兩個或更多屬性(定性變數)分類時所列出的頻數表。
(2) 示例
import numpy as np
import pandas as pd
from scipy.stats import chi2_contingency
np.random.seed(12345678)
data = np.random.randint(2, size=(40, 3)) # 2個分類,50個例項,3個特徵
data = pd.DataFrame(data, columns=['A', 'B', 'C'])
contingency = pd.crosstab(data['A'], data['B']) # 建立列聯表
print(chi2_contingency(contingency)) # 卡方檢驗
'''
執行結果:
(0.36556036556036503, 0.54543425102570975, 1,
array([[ 10.45, 8.55],
[ 11.55, 9.45]]))'''
(3) 結果分析
卡方檢驗函式的引數是列聯表中的頻數,返回結果第一個值為統計量值,第二個結果為p-value值,p-value=0.54543425102570975,比指定的顯著水平(一般5%)大,不能拒絕原假設,即相關性不顯著。第三個結果是自由度,第四個結果的陣列是列聯表的期望值分佈。
14. 單變數統計分析
(1) 用途
單變數統計描述是資料分析中最簡單的形式,其中被分析的資料只包含一個變數,不處理原因或關係。單變數分析的主要目的是通過對資料的統計描述瞭解當前資料的基本情況,並找出資料的分佈模型。
單變數資料統計描述從集中趨勢上看,指標有:均值,中位數,分位數,眾數;從離散程度上看,指標有:極差、四分位數、方差、標準差、協方差、變異係數,從分佈上看,有偏度,峰度等。需要考慮的還有極大值,極小值(數值型變數)和頻數,構成比(分類或等級變數)。
此外,還可以用統計圖直觀展示資料分佈特徵,如:柱狀圖、正方圖、箱式圖、頻率多邊形和餅狀圖。
15. 多元線性迴歸
(1) 用途
多元線性迴歸模型(multivariable linear regression model ),因變數Y(計量資料)往往受到多個變數X的影響,多元線性迴歸模型用於計算各個自變數對因變數的影響程度,可以認為是對多維空間中的點做線性擬合。
(2) 示例
import statsmodels.api as sm
data = sm.datasets.ccard.load_pandas().data
model = sm.OLS(endog = data['AVGEXP'], exog = data[['AGE','INCOME','INCOMESQ','OWNRENT']]).fit()
print(model.summary())
'''
執行結果:
OLS Regression Results
==============================================================================
Dep. Variable: AVGEXP R-squared: 0.543
Model: OLS Adj. R-squared: 0.516
Method: Least Squares F-statistic: 20.22
Date: Thu, 31 Jan 2019 Prob (F-statistic): 5.24e-11
Time: 15:11:29 Log-Likelihood: -507.24
No. Observations: 72 AIC: 1022.
Df Residuals: 68 BIC: 1032.
Df Model: 4
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
AGE -6.8112 4.551 -1.497 0.139 -15.892 2.270
INCOME 175.8245 63.743 2.758 0.007 48.628 303.021
INCOMESQ -9.7235 6.030 -1.613 0.111 -21.756 2.309
OWNRENT 54.7496 80.044 0.684 0.496 -104.977 214.476
==============================================================================
Omnibus: 76.325 Durbin-Watson: 1.692
Prob(Omnibus): 0.000 Jarque-Bera (JB): 649.447
Skew: 3.194 Prob(JB): 9.42e-142
Kurtosis: 16.255 Cond. No. 87.5
==============================================================================
'''
(3) 結果分析
直接通過返回結果中各變數的P值與0.05比較,來判定對應的解釋變數的顯著性,P<0.05則認為自變數具有統計學意義,從上例中可以看到收入INCOME最有顯著性。
16. 邏輯迴歸
(1) 用途
當因變數Y為2分類變數(或多分類變數時)可以用相應的logistic迴歸分析各個自變數對因變數的影響程度。
(2) 示例
import statsmodels.api as sm
data = sm.datasets.ccard.load_pandas().data
data['OWNRENT'] = data['OWNRENT'].astype(int)
model = sm.Logit(endog = data['OWNRENT'], exog = data[['AVGEXP','AGE','INCOME','INCOMESQ']]).fit()
print(model.summary())
'''
執行結果:
Optimization terminated successfully.
Current function value: 0.504920
Iterations 8
Logit Regression Results
==============================================================================
Dep. Variable: OWNRENT No. Observations: 72
Model: Logit Df Residuals: 68
Method: MLE Df Model: 3
Date: Fri, 01 Feb 2019 Pseudo R-squ.: 0.2368
Time: 17:05:47 Log-Likelihood: -36.354
converged: True LL-Null: -47.633
LLR p-value: 4.995e-05
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
AVGEXP 0.0002 0.001 0.228 0.820 -0.002 0.002
AGE 0.0853 0.042 2.021 0.043 0.003 0.168
INCOME -2.5798 0.822 -3.137 0.002 -4.191 -0.968
INCOMESQ 0.4243 0.126 3.381 0.001 0.178 0.670
==============================================================================
'''
(3) 結果分析
直接通過返回結果中各變數的P值與0.05比較,來判定對應的解釋變數的顯著性,P<0.05則認為自變數具有統計學意義。
