python機器學習筆記:EM演算法
EM演算法也稱期望最大化(Expectation-Maximum,簡稱EM)演算法,它是一個基礎演算法,是很多機器學習領域的基礎,比如隱式馬爾科夫演算法(HMM),LDA主題模型的變分推斷演算法等等。本文對於EM演算法,我們主要從以下三個方向學習:
- 1,最大似然
- 2,EM演算法思想及其推導
- 3,GMM(高斯混合模型)
1,最大似然概率
我們經常會從樣本觀察資料中,找到樣本的模型引數。最常用的方法就是極大化模型分佈的對數似然函式。怎麼理解呢?下面看我一一道來。
假設我們需要調查我們學習的男生和女生的身高分佈。你會怎麼做啊?你說那麼多人不可能一個一個的去問吧,肯定是抽樣了。假設你在校園隨便捉了100個男生和100個女生。他們共200個人(也就是200個身高的樣本資料,為了方便表示,下面我們說的“人”的意思就是對應的身高)都在教室了。那麼下一步怎麼辦?你開始喊:“男的左邊,女的右邊”,然後就統計抽樣得到的100個男生的身高。假設他們的身高是服從高斯分佈的。但是這個分佈的均值 μ 和方差 σ2
用數學的語言來說就是:在學校那麼多男生(身高)中,我們獨立地按照概率密度 p(x | θ) ,我們知道了是高斯分佈 N(μ, δ)的形式,其中的未知引數是 θ = [ μ, δ ] T 。抽到的樣本集是 X={X1, X2, X3.....Xn},其中 Xi 表示抽到的第 i 個人的身高,這裡的 N 就是100,表示抽到的樣本個數。
由於每個樣本都是獨立地從 p(x | θ) 中抽取的,換句話說這 100 個男生中的任何一個,都是隨便抽取的,從我們的角度來看這些男生之間是沒有關係的。那麼,我們從學習這麼多男生中為什麼恰好抽到了這 100個人呢?抽到這 100 個人的概率是多少呢?因為這些男生(的身高)是服從同一個高斯分佈 p(x | θ)的。那麼我們抽到男生A(的身高)的概率是 p(xA
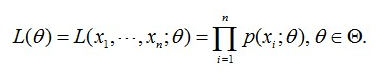
這個概率反映了,在概率密度函式的引數是 θ 時,得到 X 這組樣本的概率。因為這裡 X 是已知的,也就是說我抽取到這100個人的身高是可以測出來的,也就是已知的。而 θ 是未知的,則上面這個公式只有 θ 是未知的,所以他是關於 θ 的函式。這個函式反映的是在不同的引數 θ 的取值下,取得當前這個樣本集的可能性,因此稱為引數 θ 相對於樣本集 X 的似然函式(likehood function),記為 L(θ)。
這裡出現了一個概念,似然函式。還記得我們的目標嗎?我們需要在已經抽到這一組樣本X的條件下,估計引數 θ 的值。怎麼估計呢?似然函式有什麼用呢?我們下面先了解一下似然的概念。
直接舉個例子:
某位同學與一位獵人一起外出打獵,一隻野兔從前方竄過。只聽一聲槍響,野兔應聲倒下,如果要你推測,這一發命中的子彈是誰打的?你就會想,只發一槍便打中,由於獵人命中的概率一般大於這位同學命中的概率,所以這一槍應該是獵人射中的。
這個例子所作的推斷就體現了極大似然法的基本思想。下面再說一個最大似然估計的例子。
再例如:假設你去賭場了,但是不知道能不能賺錢,你就在門口堵著出來,出來一個人你就問人家賺錢還是賠錢,如果問了五個人,假設五個人都說自己賺錢了,那麼你就會認為,賺錢的概率肯定是非常大的。
從上面兩個例子,你得到了什麼結論?
總的來說:極大似然估計就是估計模型引數的統計學方法。
回到男生身高的例子。在學校那麼多男生中,我一抽就抽到這 100 個男生(表示身高),加入不是其他人,那是不是表示在整個學校中,這 100 個人(的身高)出現的概率最大啊,那麼這個概率怎麼表示呢?就是上面那個似然函式 L(θ)。所以我們就只需要找到一個引數 θ ,其對應的似然函式 L(θ) 最大,也就是說抽到這 100 個男生(的身高)的概率最大,這個叫做 θ 的最大似然估計量,記為:

有時,可以看到 L(Θ) 是連乘的,所以為了便於分析,還可以定義對數似然函式,將其變為連加的:
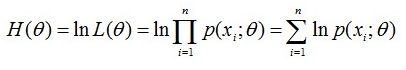
現在我們知道了,要求出 Θ ,只需要使 Θ 的似然函式 L(Θ) 極大化,然後極大值對應的 Θ 就是我們的估計。這裡就回到了求最值的問題了。怎麼求一個函式的最值?當然是求導,然後令導數為零,那麼解這個方程得到的 Θ 就是了(前提是函式L(Θ)連續可微)。那如果 Θ 是包含多個引數的向量,那麼如何處理呢?當然是求 L(Θ) 對所有引數的偏導數,也就是梯度了,那麼 n 個未知的引數,就有 n 個方程,方程組的解就是似然函式的極值點了,當然就得到了這 n 個引數了。
最後使用PPT整理一下,更直觀:


所以,其實最大似然估計你可以把它看做是一個反推。多數情況下我們是根據已知條件來推斷結果,而最大似然估計是已經知道了結果,然後尋找使該結果出現的可能性最大的條件,以此作為估計值。比如,如果其他條件一定的話,抽菸者發生肺癌的危險是不抽菸者的五倍,那麼如果我們知道有個人是肺癌,我想問你這個人是抽菸還是不抽菸。你如何判斷,你可能對這個人一無所知,你所知道的只有一件事,那就是抽菸更容易發生肺癌,那麼你會猜測這個人不抽菸嗎?我相信你更可能會說,這個人抽菸,為什麼?這就是“最大可能”,我只能說他“最有可能”是抽菸的,“他是抽菸的”這一估計才是“最有可能”得到“肺癌” 這樣的結果,這就是最大似然估計。
總結一下:極大似然估計,只是概率論在統計學的應用,它是引數估計的方法之一。說的是已知某個隨機樣本滿足某種概率分佈,但是其中具體的引數不清楚,引數估計就是通過若干次實驗,觀察其結果,利用結果推出引數的大概值。最大似然估計是建立在這樣的思想上:已知某個引數能使這個樣本出現的概率最大,我們當然不會再去選擇其他小概率的樣本,所以乾脆把這個引數作為估計的真實值。
而求最大似然估計值的一般步驟
- 1,寫出似然函式
- 2,對似然函式取對數,並整理
- 3,求導數,令導數為0,得到似然方程
- 4,解似然方程,得到的引數即為所求
2,EM演算法要解決的問題
上面說到,通過樣本觀察資料中,找到樣本的模型引數。但是在一些情況下,我們得到的觀察資料有未觀察到的隱含資料,此時我們未知的有隱含資料和模型引數,因而無法直接用極大化對數似然函式得到模型分佈的引數。怎麼辦呢?這就是EM演算法可以派上用場的地方了。
下面,我們重新回到上面那個身高分佈估計的問題。現在,通過抽取得到的那100個男生的身高和已知的其身高服從高斯分佈,我們通過最大化其似然函式,就可以得到了對應高斯分佈的引數 θ = [ μ, δ ] T 了。那麼,對於我們學習的女生的身高分佈也可以用同樣的方法得到了。
再回到例子本身,如果沒有“男的左邊,女的右邊”這個步驟,或者說這二百個人已經混到一起了,這時候,你從這二百個人(的身高)裡面隨便給我指一個人(的身高),我都無法確定這個的身高是男生的身高,還是女生的身高。也就是說你不知道抽取的那二百個人裡面的每一個人到底是從男生的那個身高分佈裡面抽取的,還是女生的那個身高分佈抽取的。用數學的語言就是:抽取的每個樣本都不知道是從那個分佈抽取的。
這個時候,對於每一個樣本或者你抽取到的人,就有兩個東西需要猜測或者估計的了,一是這個人是男生還是女的?二是男生和女生對應的身高的高斯分佈的引數是多少?
所以問題就難了。

只有當我們知道了那些人屬於同一個高斯分佈的時候,我們才能夠對這個分佈的引數做出靠譜的預測,例如剛開始的最大似然所說的,但現在兩種高斯分佈的人混在一塊了,我們又不知道那些人屬於第一個高斯分佈,那些人屬於第二個,所以就沒法估計這兩個分佈的引數。反過來,只有當我們對這兩個分佈的引數做出了準確的估計的時候,才能知道到底那些人屬於第一個分佈,那些人屬於第二個分佈。
這就成了一個先有雞還是先有蛋的問題了。雞說,沒有我,誰把你生出來的啊。蛋不服,說,沒有我你從哪蹦出來的啊。為了解決這個你依賴我,我依賴你的迴圈依賴問題,總得有一方要先打破僵局,說,不管了,我先隨便整一個值出來,看你怎麼變,然後我再根據你的變換調整我的變換,然後如此迭代著不斷互相推導,最終就會收斂到一個解,這就是EM演算法的基本思想了。
不知道大家能理解其中的思想嗎,然後再舉個例子。
例如小時候,老媽給一大袋子糖果給你,叫你和你姐姐等分,然後你懶得去點糖果的個數,所以你也就不知道每個人到底該分多少個,咱們一般怎麼做呢?先把一袋糖果目測的分為兩袋,然後把兩袋糖果拿在左右手,看那個重,如果右手重,那麼很明顯右手這袋糖果多了,然後你再在右手這袋糖果中抓一把放到左手這袋,然後再感受下那個重,然後再從重的那袋抓一小把放入輕的那一袋,繼續下去,直到你感覺兩袋糖果差不多相等了為止。然後為了體現公平,你還讓你姐姐先選。
EM演算法就是這樣,假設我們想估計A和B兩個引數,在開始狀態下二者都是未知的,但如果知道了A的資訊就可以得到B的資訊,反過來知道了B也就得到了A。可以考慮首先賦予A某種初值,以此得到B的估計值,然後從B的當前值出發,重新估計A的取值,這個過程一直持續到收斂為止。
EM 的意思是“Expectation Maximization”,在我們上面這個問題裡面,我們先隨便猜一下男生(身高)的正態分佈的引數:如均值和方差。例如男生的均值是1米7,方差是 0.1 米(當然了,剛開始肯定沒有那麼準),然後計算出每個人更可能屬於第一個還是第二個正態分佈中的(例如,這個人的身高是1米8,那很明顯,他最大可能屬於男生的那個分佈),這個是屬於Expectation 一步。有了每個人的歸屬,或者說我們已經大概地按上面的方法將這 200 個人分為男生和女生兩部分,我們就可以根據之前說的最大似然那樣,通過這些被大概分為男生的 n 個人來重新估計第一個分佈的引數,女生的那個分佈同樣方法重新估計。這個就是 Maximization。然後,當我們更新了這兩個分佈的時候,每一個屬於這兩個分佈的概率又變了,那麼我們就再需要調整 E 步、.... 如此往復,直到引數基本不再發生變化為止。
這裡把每個人(樣本)的完整描述看做是三元組 yi = {xi, zi1, zi2},其中, xi 是第 i 個樣本的觀測值,也就是對應的這個人的身高,是可以觀測到的值。zi1和zi2表示男生和女生這兩個高斯分佈中哪個被用來產生值 xi,就是說這兩個值標記這個人到底是男生還是女生(的身高分佈產生的)。這兩個值我們是不知道的,是隱含變數。確切的說, zij 在 xi 由第 j個高斯分佈產生時值為1,否則為0。例如一個樣本的觀測值為 1.8,然後他來自男生的那個高斯分佈,那麼我們可以將這個樣本表示為 {1.8, 1, 0}。如果 zi1 和 zi2的值已知,也就是說每個人我已經標記為男生或者女生了,那麼我們就可以利用上面說的最大似然演算法來估計他們各自高斯分佈的引數。但是他們未知,所以我們只能用 EM演算法。
咱們現在不是因為那個噁心的隱含變數(抽取得到的每隔樣本都不知道是那個分佈抽取的)使得本來簡單的可以求解的問題變複雜了,求解不了嗎。那怎麼辦呢?人類解決問題的思路都是想能否把複雜的問題簡單化。好,那麼現在把這個複雜的問題逆回來,我假設已經知道這個隱含變量了,哎,那麼求解那個分佈的引數是不是很容易了,直接按上面說的最大似然估計就好了。那你就問我了,這個隱含變數是未知的,你怎麼就來一個假設說已知呢?你這種假設是沒有依據的。所以我們可以先給這個分佈弄一個初始值,然後求這個隱含變數的期望,當成是這個隱含變數的已知值,那麼現在就可以用最大似然求解那個分佈的引數了吧,那假設這個引數比之前的那個隨機的引數要好,它更能表達真實的分佈,那麼我們再通過這個引數確定的分佈去求這個隱含變數的期望,然後再最大化,得到另一個更優的引數,...迭代,就能得到一個皆大歡喜的結果了。
這裡最後總結一下EM演算法的思路:

所以EM演算法解決問題的思路就是使用啟發式的迭代方法,既然我們無法直接求出模型分佈引數,那麼我們可以先猜想隱含資料(EM演算法的E步),接著基於觀察資料和猜測的隱含資料一起來極大化對數似然,求解我們的模型引數(EM演算法的M步)。由於我們之前的隱藏資料是猜測的,所以此時得到的模型引數一般還不是我們想要的結果。不過沒關係,我們基於當前得到的模型引數,繼續猜測隱含資料(EM演算法的E步),然後繼續極大化對數似然,求解我們的模型引數(EM演算法的M步)。以此類推,不斷的迭代下去,直到模型分佈引數基本無變化,演算法收斂,找到合適的模型引數。
下面再看看本文中EM演算法最後一個例子:拋硬幣
Nature Biotech在他的一篇EM tutorial文章《Do, C. B., & Batzoglou, S. (2008). What is the expectation maximization algorithm?. Nature biotechnology, 26(8), 897.》中,用了一個投硬幣的例子來講EM演算法的思想。
比如兩枚硬幣A和B,如果知道每次拋的是A還是B,那可以直接估計(見下圖a)。

如果不知道拋的是A還是B(這時就刺激了吧,對的,這就是咱們不知情的隱變數),只觀測到5輪迴圈每輪迴圈10次,共計50次投幣的結果,這時就沒法直接估計A和B的正面概率。這時,就輪到EM演算法出場了(見下圖b)。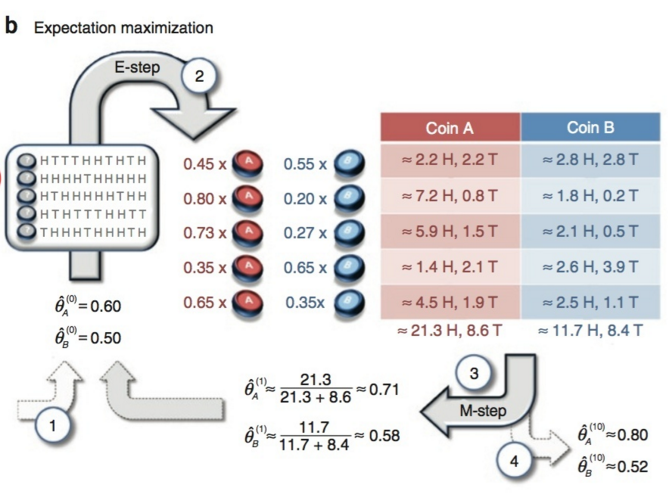
可能直接看,這個例子不好懂,下面我們來通俗化這個例子。
還是兩枚硬幣A和B,假定隨機拋擲後正面朝上概率分別為PA,PB。我們就不拋了,直接使用上面的結果,每一輪都是拋10次,總共5輪:
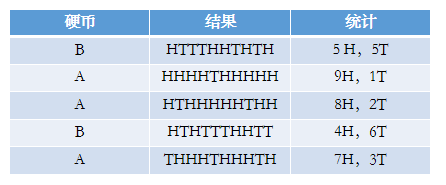
硬幣A被拋了30次,在第二輪,第三輪,第五輪分別出現了9次,8次,7次正,所以很容易估計出PA,類似的PB 也很容易計算出來,如下:

但是問題來了,如果我們不知道拋的硬幣是A還是B呢(即硬幣種類是隱變數),然後再輪流拋五次,得到如下的結果呢?
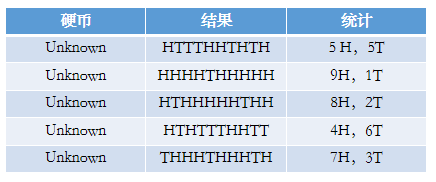
下面問題變得有意思了,現在我們的目標還是沒有變,還是估計PA和PB,需要怎麼做呢?
思路如下:
顯然這裡我們多了一個硬幣種類的隱變數,設為 z,可以把它看做一個10維的向量(z1, z2, ...z10),代表每次投擲時所使用的硬幣,比如z1,就代表第一輪投擲時使用的硬幣是A還是B。
- 但是,這個變數Z不知道,就無法去估計PA和PB,所以我們先必須估計出Z,然後才能進一步估計PA和PB。
- 可是要估計Z,我們又得知道PA和PB,這樣我們才能用極大似然概率法去估計Z,這不是前面提的雞生蛋和蛋生雞的問題嗎,如何解?
答案就是先隨機初始化一個PA和PB,用它來估計Z,然後基於Z,還是按照最大似然概率法則去估計新的PA和PB,如果新的PA和PB和我們初始化的PA和PB一樣,請問這說明了什麼?
這說明我們初始化的PA和PB是一個相當靠譜的估計!
這就是說,我們初始化的PA和PB,按照最大似然概率就可以估計出Z,然後基於Z,按照最大似然概率可以反過來估計出P1和P2,當與我們初始化的PA和PB一樣時,說明是P1和P2很可能就是真實的值。這裡包含了兩個互動的最大似然估計。
如果新估計出來的PA和PB和我們初始化的值差別很大,怎麼辦呢?就是繼續用新的P1和P2迭代,直至收斂。
做法如下:
我們不妨,這樣,先隨便給PA和PB賦一個值,比如:

所以我們的初始值 theta 為:

然後,我們看看第一輪拋擲最可能是哪個硬幣,(五正五負):

其實上式很簡單就是:PA= 0.6*0.6*0.6*0.6*0.6*0.4*0.4*0.4*0.4*0.4 = 0.0007962624000000002(後面類似)
PB= 0.5**10 = 0.0009765625
然後求出選擇PA的概率和PB的概率值

然後依次求出其他四輪中相應的概率。做成表格如下:
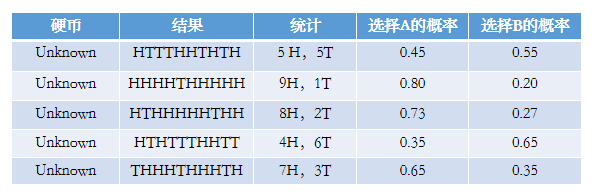
然後我們通過上面的概率值來估計Z,大概是這樣的:

這樣我們通過最大似然估計法則就估算出來PA和PB的值了,如下:
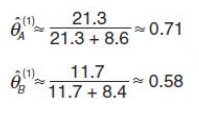
然後我們再次迭代,繼續估算,假設我們估算到第10次,就算出PA和PB的值是正確的了,如下:
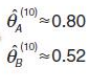
下面我們來對比初始化的PA和PB和新估計的PA和PB,和最終的PA和PB:

我們可以發現,我們估計的PA和PB相比於他們的初始值,更接近於他們的真實值,就這樣不斷迭代,不斷接近真實值,這就是EM演算法的奇妙之處。
可以期待,我們繼續按照上面的思路,用估計出的PA和PB再來估計Z,再用Z來估計新的PA和PB,反覆迭代下去,就可以最終得到PA和PB的真值了。而這裡我們假設為 0.8 和 0.52。此時無論怎麼迭代,PA和PB的值都會保持在 0.8和0.52不變,於是,我們就找到了PA和PB的最大似然估計。
下面在推導EM演算法之前,我們先學習一下Jensen不等式
3,導數性質和Jensen不等式
在學習Jensen不等式之前,我們先說說二階導數的一些性質。
3.1,二階導數的性質1
如果有一個函式 f(x) 在某個區間 I 上有 f ''(x)(即二階導數) > 0 恆成立,那麼對於區間 I上的任意 x, y 總有:

如果總有 f''(x) < 0 成立,那麼上式的不等號反向。
幾何的直觀解釋:如果有一個函式 f(x) 在某個區間 I 上有 f ''(x)(即二階導數) > 0 恆成立,那麼在區間 I 上 f(x)的影象上的任意兩點連出的一條線段,這兩點之間的函式影象都在該線段的下方,反之在該線段的上方。
3.2,二階導數的性質2:判斷函式極大值以及極小值
結合一階,二階導數可以求函式的極值。當一階導數等於0,而二階導數大於0時,為極小值點。當一階導數等於0,而二階導數小於0時,為極大值點;當一階導數和二階導數都等於0,為駐點 。
駐點:在微積分,駐點(Stationary Point)又稱為平穩點、穩定點或臨界點(Critical Point)是函式的一階導數為零,即在“這一點”,函式的輸出值停止增加或減少。對於一維函式的影象,駐點的切線平行於x軸。對於二維函式的影象,駐點的切平面平行於xy平面。值得注意的是,一個函式的駐點不一定是這個函式的極值點(考慮到這一點左右一階導數符號不改變的情況);反過來,在某設定區域內,一個函式的極值點也不一定是這個函式的駐點(考慮到邊界條件),駐點(紅色)與拐點(藍色),這影象的駐點都是區域性極大值或區域性極小值
3.3,二階導數的性質3:函式凹凸性
設 f(x) 在 [a, b] 上連續,在(a, b)內具有一階和二階導數,那麼:
- (1)若在(a, b)內 f ''(x) > 0,則 f(x) 在[a, b]上的圖形是凹的
- (2)若在(a, b)內 f ''(x) < 0,則 f(x) 在[a, b]上的圖形是凸的
3.4 期望
在概率論和統計學中,數學期望(mean)(或均值,也簡稱期望)是實驗中每次可能結果的概率乘以其結果的總和,是最基本的數學特徵之一。它反映隨機變數平均取值的大小。
需要注意的是:期望值並不一定等同於常識中的“期望”——“期望值”也許與每一個結果都不相等。期望值是該變數輸出值的平均數。期望值並不一定包含於變數的輸出值集合裡。
大數定理規定:隨著重複次數接近無窮大,數值的算術平均值幾乎肯定地收斂於期望值。
離散型:
如果隨機變數只取得有限個數或無窮能按一定次序一一列出,其值域為一個或若干個有限或無限區域,這樣的隨機變數稱為離散型隨機變數。
離散型隨機變數只取得有限個值或無窮能按一定次序一一列出,其值域為一個或若干個有限或無限區間,這樣的隨機變數稱為離散型隨機變數。
離散型隨機變數的一切可能的取值 xi 與對應的概率 p(xi) 乘積之和稱為該離散型隨機變數的數學期望(若該求和絕對收斂),記為E(x)。它是簡單算術平均的一種推廣,類似加權平均。
公式:
離散型隨機變數X的取值為X1, X2, X3....Xn, p(X1),p(X2), p(X3)....P(Xn)為X對應取值的概率,可以理解為資料 X1, X2, X3.....Xn出現的頻率 f(Xi),則:
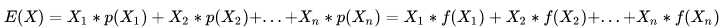
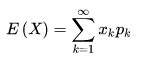
例子:
某城市有10萬個家庭,沒有孩子的家庭有 1000 個,有一個孩子的家庭有 9 萬個,有兩個孩子的家庭有 6000個,有 3個孩子的家庭有 3000個。
則此城市中任一個家庭中孩子的數目是一個隨機變數,記為X。它可取值 0, 1, 2, 3 。
其中,X取 0 的概率為 0.01 ,取 1的概率為 0.9,取 2的概率為0.06,取 3的概率為0.03
則它的數學期望為:
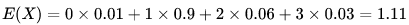
即此城市一個家庭平均有小孩 1.11 個,當然人不可能用1.11來算,約等於2個。
設 Y 是隨機變數X的函式:
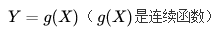
它的分佈律為:
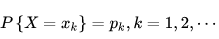

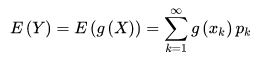
連續型:
設連續型隨機變數 X 的概率密度函式為 f(x),若積分絕對收斂,則稱積分的值為隨機變數的數學期望,記為 E(x),即:
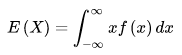
若隨機變數 X的分佈函式 F(x) 可表示成一個非負可積函式 f(x)的積分,則稱 X為連續型隨機變數,f(x)稱為 X 的概率密度函式(分佈密度函式)。
數學期望 E(X) 完全由隨機變數 X 的概率分佈所確定。若X服從某一分佈,也稱 E(X) 是這一分佈的數學期望。
定理:
若隨機變數 Y 符合函式 Y = g(x),且下面函式絕對收斂,則有下下面的期望

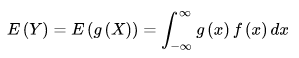
該定理的意義在於:我們求 E(Y) 時不需要計算出 Y的分佈律或概率分佈,只要利用X的分佈律或者概率密度即可。
上述定理還可以推廣到兩個或以上隨機變數的函式情況。
設 Z 是隨機變數 X, Y 的函式 Z = g(X, Y)(g是連續函式),Z是一個一維隨機變數,二維隨機變數(X, Y)的概率密度為 f(x, y),則有:
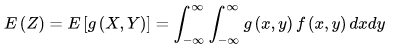
離散型隨機變數與連續型隨機變數的區別
離散型隨機變數與連續型隨機變數都是由隨機變數取值範圍確定。
變數取值只能取離散型的自然數,就是離散型隨機變數。例如,一次擲20個硬幣,k額硬幣正面朝上,k是隨機變數。k的取值只能是自然數0, 1, 2 ,3, 4, 。。。。20。而不能取小數 3.5 ,無理數 √ 20 ,因此k是離散型隨機變數。
如果變數可以在某個區間內取任一實數,即變數的取值可以是連續的,這隨機變數就稱為連續型變數。例如公共汽車每 15 分鐘一班,某人在站臺等車時間 x 是個隨機變數,x的取值範圍是 [0, 15),它是一個區間,從理論上說在這個區間內可取任一實數 3.5 ,無理數 ,√ 20 等,因而稱這隨機變數是連續型隨機變數。
3.5 Jensen不等式

如果用圖表示會很清晰:


4,EM演算法的推導
從上面的總結,我們知道EM演算法就是迭代求解最大值的演算法,同時演算法在每一次迭代時分為兩步,E步和M步。一輪輪迭代更新隱含資料和模型分佈引數,直到收斂,即得到我們需要的模型引數。
這時候你就不服了,說你老迭代迭代的,你咋知道新的引數的估計就比原來的好啊?為什麼這種方法行得通呢?有沒有失效的時候呢?什麼時候失效呢?用到這個方法需要注意什麼問題呢?
為了說明這一串問題,我們下面學習EM演算法的整個推導過程。
首先,我們接著上面的問題聊,就是100名學生的身高問題,總結一下問題,如下:
樣本集 {x(1), x(2) , .... x(m)},包含 m 個獨立的樣本,其中每個樣本 i 對應的類別 z(i) 是未知的,所以很難用極大似然求解。而我們的目的就是想找到每個樣例隱含的類別z,能使得p(x, z) 最大。
p(x, z) 的最大似然估計如下:
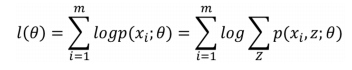
上式中,我們要考慮每個樣本在各個分佈中的情況。本來正常求偏導就可以了,但是因為有隱含資料的存在,也就是log後面還有求和,這個就沒有辦法直接求出 theta了。
對於每一個樣例 i,讓Qi 表示該樣例隱含變數 z 的某種分佈,Qi 滿足的條件是:

如果 z 是連續性的,那麼Qi是概率密度函式,需要將求和符號換做積分符號。繼續上面的例子,假設隱藏變數 z是身高,那就是連續的高斯分佈;假設隱藏變數是男女,那就是伯努利分佈 。
所以說如果我們確定了隱藏變數z,那求解就容易了,可是怎麼求解呢?這就需要一些特殊的技巧了。
技巧:Jensen不等式應用於凹函式時,不等號方向反向。
我們知道:

所以對右式分子分母同時乘以 Q(z):
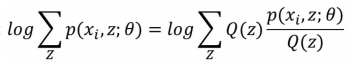
為什麼要這麼做呢?說白了就是要湊Jensen不等式(Q(z) 是Z的分佈函式),下面繼續
這裡假設:
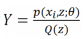
則上式可以寫為:
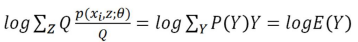
我們由Jensen不等式可以知道(由於對數函式是凹函式):
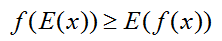
則代入 上式:
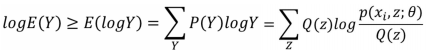
所以:
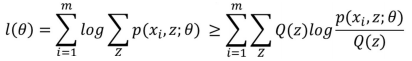
上面這個過程可以看做是對 l(Θ) 求了下界。對於Qi 的選擇,有多種可能,那種更好呢?假設 Θ 已經給定,那麼 l(Θ) 的值就取決於 Q(z)和P(x, z)了。
4.1 如何優化下界?
因為下界比較好求,所以我們要優化這個下界來使得似然函式最大。那麼如何優化下界呢?
隨著我們的引數變換,我們的下界是不斷增大的趨勢。我們紅色的線是恆大於零的。簡單來說,就是EM演算法可以看做是J 的座標上升法,E步固定 theta,優化 Q,M步固定Q,優化 theta。
迭代到收斂

可能用這個圖更明顯(參考:https://blog.csdn.net/u010834867/article/details/90762296)
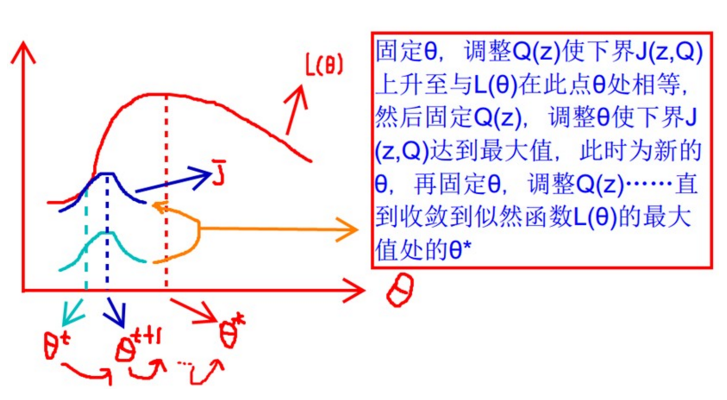
我們需要調整上式中Q(z)和P(x, z) 這兩個概率,使下界不斷上升,以逼近 l(Θ) 的真實值,那麼什麼時候算是調整好了呢?當不等式變成等式時,說明我們調整後的概率能夠等價於 l(Θ) 了。按照這個思路,我們要找到等式成立的條件。根據Jensen不等式,要想讓等式成立,就需要什麼呢?下面繼續說。
4.2 如何能使Jensen不等式等號成立呢?
什麼時候,使得我們的似然函式最大呢?當然是取等號的時候。什麼時候等號成立呢?
由上面Jensen不等式中所說,我們要滿足Jensen不等式的等號,則當且僅當 P(x=E(x)) = 1的時候,也就是說隨機變數X是常量。在這裡,我們則有:
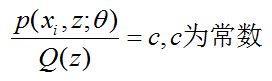
c為常數,不依賴於 z。對此式子做進一步推導,由於Q(z) 是z的分佈函式,所以滿足:

所有的分子和等於常數C(分母相同),即:

多個等式分子分母相加不變,這個認為每個樣例的兩個概率比值都是 c,那麼就可以求解 Q(z)了。
4.3 Q(z)的求解
我們知道Q(z) 是z的分佈函式,而且:
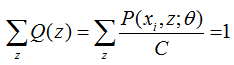
由上式就可得C就是 P(xi, z)對Z求和,我們上面有公式。
從上面兩式,我們可以得到:
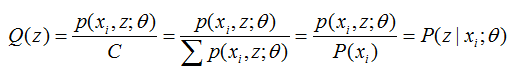
Q(z) 代表第 i 個數據是來自 zi 的概率。
至此,我們推出了在固定其他引數 Θ 後,Q(z)的計算公式就是後驗概率,解決了Q(z)如何選擇的問題。這一步就是E步,建立 l(Θ) 的下界。
所以去掉 l(Θ) 式中為常數的部分,則我們需要極大化的對數似然下界為:
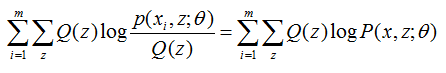
注意上式也就是我們EM演算法的M步,就是在給定 Q(z)後,調整Θ,去極大化 l(Θ)的下界(在固定Q(z)後,下界還可以調整的更大)。
E步我們再強調一次,注意到上式Q(z)是一個分佈,因此 下式可以理解為 logP(x, z; Θ) 基於條件概率分佈 Q(z)的期望。

至此,我們學習了EM演算法那中E步和M步的具體數學含義。
5,EM演算法的一般流程
下面我們總結一下EM演算法的流程。
輸入:觀察資料 x = {x1, x2, ... xm},聯合分佈 p(x, z; θ),條件分佈 p(z|x; θ),最大迭代次數 J 。
1)隨機初始化模型引數 θ 的初值 θ0。
2)迴圈重複,即for j from 1 to J 開始EM演算法迭代。
E步:計算聯合分佈的條件概率期望
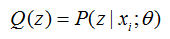
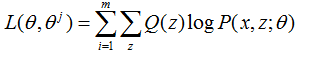
M步:極大化L(θ, θj),得到 θj+1:
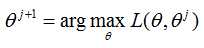
3)如果 θj+1 已經收斂,則演算法結束,否則繼續回到步驟E步迭代。
輸出:模型引數 θ。
用PPT總結如下:

6,EM演算法的收斂性思考
(這裡直接貼上劉建平老師的部落格了。方便。。)
EM演算法的流程並不複雜,但是還有兩個問題需要我們思考:
- 1) EM演算法能保證收斂嗎?
- 2)EM演算法如果收斂,那麼能保證收斂到全域性最大值嗎?
首先,我們先看第一個問題,EM演算法的收斂性。要證明EM演算法收斂,則我們需要證明我們的對數似然函式的值在迭代的過程中一直在增大。即:
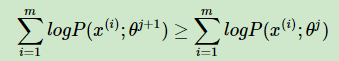
由於:
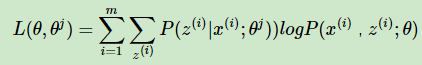
令:
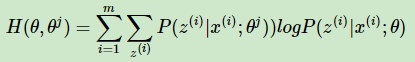
上面兩個式子相減得到:

在上式中分別取 Θ 為 Θj 和 Θj+1 ,並且相減得到:
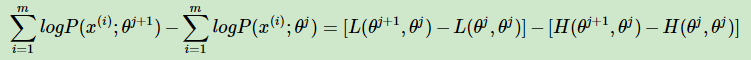
要證明EM演算法的收斂性,我們只需要證明上式的右邊是非負的即可。
由於 Θj+1 使得L(Θ,Θj )極大,因此有:
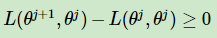
上式的意思是說極大似然估計單調遞增,那麼我們會達到最大似然估計的最大值。
而對於第二部分,我們有:
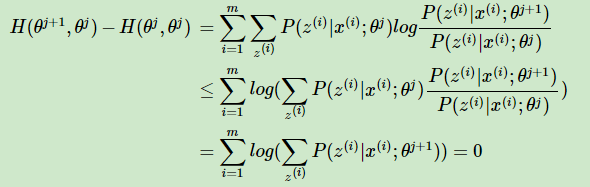
上式中,第二個不等式使用了Jensen不等式,只不過和前面的使用相反而已,最後一個等式使用了概率分佈累積為1的性質。
至此,我們得到了:
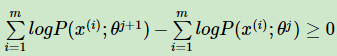
從上面的推導可以看出,EM演算法可以保證收斂到一個穩定點,但是卻不能保證收斂到全域性的極大值點,因此它是區域性最優的演算法,當然,如果我們的優化目標 L(Θ,Θj )是凸的,則EM演算法可以保證收斂到全域性最大值,這點和梯度下降法這樣的迭代演算法相同。至此我們也回答了上面的第二個問題。
如果我們從演算法思想的角度來思考 EM 演算法,我們可以發現我們的演算法裡已知的是觀察資料,未知的隱含資料和模型引數。在E步,我們所做的事情是固定模型引數的值,優化隱含資料的分佈,而在M步,我們所做的事情是固定隱含資料分佈,優化模型引數的值。比較下其他的機器學習演算法,其實很多演算法都有類似的思想。比如SMO演算法,座標軸下降法都是由了類似的思想來求解問題。
7,GMM(高斯混合模型)
我們上面已經推導了EM演算法,下面再來說一下高斯混合模型。高斯混合模型是什麼呢?顧名思義就是用多個高斯模型來描述資料的分佈,就是說我們的資料可以看做是從多個Gaussian Distribution 中生成出來的。那GMM是由K個Gaussian分佈組成,所以每個Gaussian稱為一個“Component”。
首先說一句,為什麼是高斯混合模型呢?而不是其他模型呢?
因為從中心極限定理知:只要k足夠大,模型足夠複雜,樣本量足夠多,每一塊小區域就可以用高斯分佈描述(簡單說:只要樣本量足夠大時,樣本均值的分佈慢慢變為正態分佈)。而且高斯函式具有良好的計算效能,所以GMM被廣泛的應用。
有時候單一的高斯分佈不能很好的描述分佈,如下圖,二維高斯密度函式的等概率先為橢圓(當然後面會做練習)

從上圖我們看到,左圖用單一高斯分佈去描述,顯然沒有右圖用兩個高斯分佈去描述的效果好。
所以我們引入混合高斯模型。
如下圖所示,我們用三個高斯分佈去描述一個二維的資料:

現在我們定義 K 個高斯密度疊加:
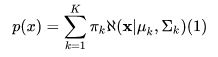
對於每個高斯密度函式有自己的均值 μk 和方差 ∑k , πk作為混合的比例係數有:
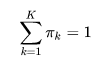
下圖中(a)為不同混合比例下的高斯概率密度分佈;(b)為混合狀態下的概率密度分佈;(c)為概率密度分佈的表面圖:

所以 p(x) 可以改寫為:
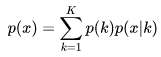
並與公式(1)對比,有:

則後驗概率 p(k|x),根據貝葉斯理論,可表示為:
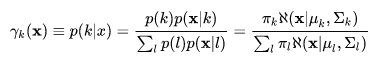
因此GMM由 μ, ∑ , π 確定,並在有引數 K的存在。
而GMM模型的求解方式和EM演算法是一樣的,就是不斷的迭代更新下去。一個最直觀的瞭解演算法的思路就是參考K-Means演算法。部落格地址:
Python機器學習筆記:K-Means演算法,DBSCAN演算法
這裡再簡單的說一下,在K-Means聚類時,每個聚類簇的質心是隱含資料。我們會假設K個初始化質心,即EM演算法的E步;然後計算得到每個樣本最近的質心,並且把樣本聚類到最近的這個質心,即EM演算法的M步,重複這個E步和M步,知道質心不再變化為止,這樣就完成了K-Means聚類。當然K-Means演算法是比較簡單的,實際問題並沒有這麼簡單,但是大概可以說明EM演算法的思想了。
上面遺留了一個問題,就是單一的高斯分佈不能很好的描述分佈,而兩個高斯分佈描述的好。為了將這個說的透徹,我們這樣做:我們生成四簇資料,其中兩簇資料離的特別近,然後我們看看K-Means演算法是否能將這兩簇離的特別近的資料按照我們的想法區分開,再看看GMM演算法呢,如果可以區分,那麼我們將資料拉伸呢?
所以下面我們會做兩個實驗,對於隨機生成的資料,我們會做K-Means演算法和GMM演算法的效果比對,然後再對資料進行處理,再做K-Means演算法和GMM演算法的效果比對。
首先生成四簇資料,效果如下:
from sklearn.datasets.samples_generator import make_blobs from matplotlib import pyplot as plt from sklearn.cluster import KMeans from sklearn.mixture import GaussianMixture # 生成新的資料 X, y_true = make_blobs(n_samples=800, centers=4, random_state=11) plt.scatter(X[:, 0], X[:, 1])
圖如下:
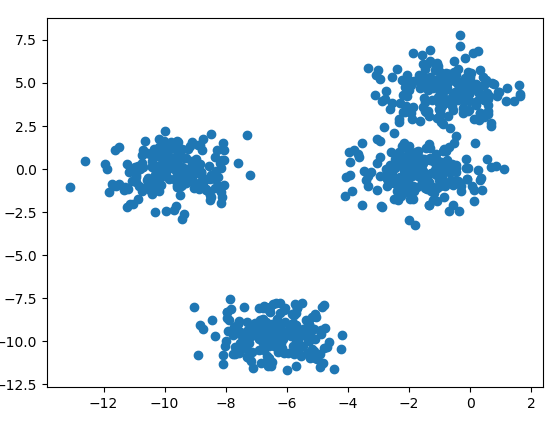
我們看看K-Means分類效果:

我們再看看GMM演算法的效果:

都能分出來,這樣很好,下面我們對資料進行處理:拉伸
rng = np.random.RandomState(13) X_stretched = np.dot(X, rng.randn(2, 2))
我們拉伸後,看看原圖效果:
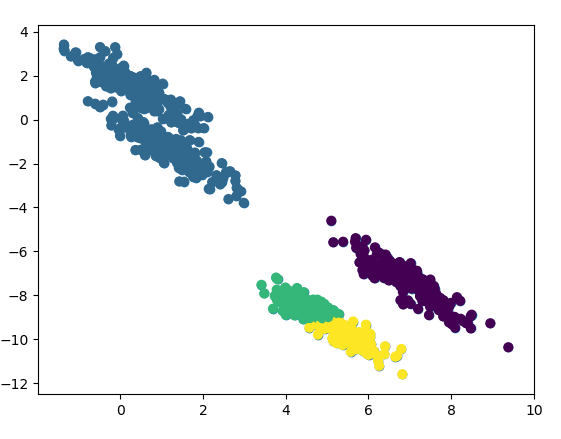
下面分別使用K-Means演算法和GMM演算法看效果:
首先是K-Means演算法
kmeans = KMeans(n_clusters=4) kmeans.fit(X) y_kmeans = kmeans.predict(X) plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
效果如下

K-Means演算法沒有把拉伸的資料分開,而是按照聚類的思想,將上面的資料聚在一起,將下面的資料聚在一起。
我們再看看GMM演算法的效果:
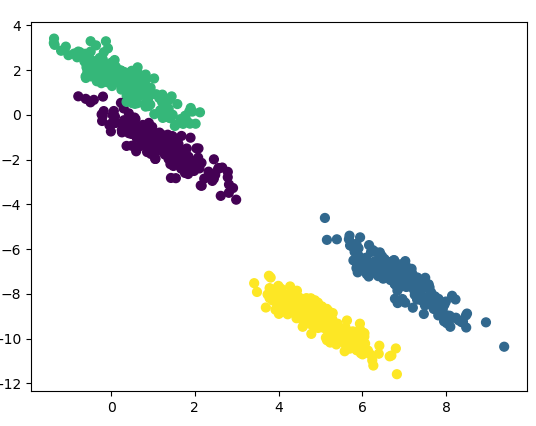
是不是GMM演算法區分出來我們想要的效果了。所以在這個問題上GMM演算法的優勢就體現出來了。
完整程式碼去我的GitHub上拿(地址:https://github.com/LeBron-Jian/MachineLearningNote)。
8,Sklearn實現GMM(高斯混合模型)
Sklearn庫GaussianMixture類是EM演算法在混合高斯分佈的實現,現在簡單記錄下其引數說明。
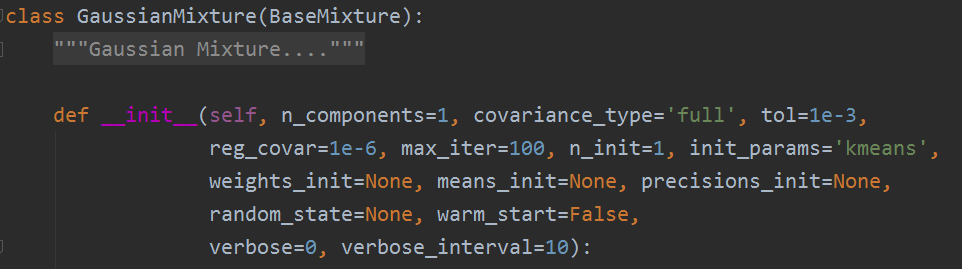
對此原始碼中的引數,我們瞭解其意義:
- 1. n_components:混合高斯模型個數,預設為1
- 2. covariance_type:協方差型別,包括{‘full’,‘tied’, ‘diag’, ‘spherical’}四種,分別對應完全協方差矩陣(元素都不為零),相同的完全協方差矩陣(HMM會用到),對角協方差矩陣(非對角為零,對角不為零),球面協方差矩陣(非對角為零,對角完全相同,球面特性),預設‘full’ 完全協方差矩陣
- 3. tol:EM迭代停止閾值,預設為1e-3.
- 4. reg_covar:協方差對角非負正則化,保證協方差矩陣均為正,預設為0
- 5. max_iter:最大迭代次數,預設100
- 6. n_init:初始化次數,用於產生最佳初始引數,預設為1
- 7. init_params: {‘kmeans’, ‘random’}, defaults to ‘kmeans’.初始化引數實現方式,預設用kmeans實現,也可以選擇隨機產生
- 8. weights_init:各組成模型的先驗權重,可以自己設,預設按照7產生
- 9. means_init:初始化均值,同8
- 10. precisions_init:初始化精確度(模型個數,特徵個數),預設按照7實現
- 11. random_state :隨機數發生器
- 12. warm_start :若為True,則fit()呼叫會以上一次fit()的結果作為初始化引數,適合相同問題多次fit的情況,能加速收斂,預設為False。
- 13. verbose :使能迭代資訊顯示,預設為0,可以為1或者大於1(顯示的資訊不同)
- 14. verbose_interval :與13掛鉤,若使能迭代資訊顯示,設定多少次迭代後顯示資訊,預設10次。
下面看看網友對原始碼的分析:
(1)首先將模型完全轉換成對數計算,根據高斯密度函式公式分別計算k個組成高斯模型的log值,即logP(x|z)的值
def _estimate_log_gaussian_prob(X, means, precisions_chol, covariance_type):
# 計算精度矩陣的1/2次方log_det(程式碼精度矩陣是通過cholesky獲取)
log_det = _compute_log_det_cholesky(
precisions_chol, covariance_type, n_features)
# 對應上面四種協方差型別,分別計算精度矩陣與(x-u)相乘那部分log_prob
if covariance_type == 'full':
log_prob = np.empty((n_samples, n_components))
for k, (mu, prec_chol) in enumerate(zip(means, precisions_chol)):
y = np.dot(X, prec_chol) - np.dot(mu, prec_chol)
log_prob[:, k] = np.sum(np.square(y), axis=1)
elif covariance_type == 'tied':
log_prob = np.empty((n_samples, n_components))
for k, mu in enumerate(means):
y = np.dot(X, precisions_chol) - np.dot(mu, precisions_chol)
log_prob[:, k] = np.sum(np.square(y), axis=1)
elif covariance_type == 'diag':
precisions = precisions_chol ** 2
log_prob = (np.sum((means ** 2 * precisions), 1) -
2. * np.dot(X, (means * precisions).T) +
np.dot(X ** 2, precisions.T))
elif covariance_type == 'spherical':
precisions = precisions_chol ** 2
log_prob = (np.sum(means ** 2, 1) * precisions -
2 * np.dot(X, means.T * precisions) +
np.outer(row_norms(X, squared=True), precisions))
# 最後計算出logP(x|z)的值
return -.5 * (n_features * np.log(2 * np.pi) + log_prob) + log_det
(2)P(x|z)*P(z)計算每個模型的概率分佈P(x,z),求對數則就是相加了
def _estimate_weighted_log_prob(self, X):
return self._estimate_log_prob(X) + self._estimate_log_weights()
(3)最後開始計算每個模型的後驗概率logP(z|x),即Q函式
def _estimate_log_prob_resp(self, X):
weighted_log_prob = self._estimate_weighted_log_prob(X)
#計算P(X)
log_prob_norm = logsumexp(weighted_log_prob, axis=1)
with np.errstate(under='ignore'):
# 忽略下溢,計算每個高斯模型的後驗概率,即佔比,對數則相減
log_resp = weighted_log_prob - log_prob_norm[:, np.newaxis]
return log_prob_norm, log_resp
(4)呼叫以上函式
#返回所有樣本的概率均值,及每個高斯分佈的Q值
def _e_step(self, X):
log_prob_norm, log_resp = self._estimate_log_prob_resp(X)
return np.mean(log_prob_norm), log_resp
2.對應M step
def _m_step(self, X, log_resp):
#根據上面獲得的每個高斯模型的Q值(log_resp)。重新估算均值self.means_,協方差self.covariances_,當前符合各高斯模型的樣本數目self.weights_(函式名起的像權重,實際指的是數目)
n_samples, _ = X.shape
self.weights_, self.means_, self.covariances_ = (
_estimate_gaussian_parameters(X, np.exp(log_resp), self.reg_covar,
self.covariance_type))
#更新當前各高斯模型的先驗概率,即P(Z)
self.weights_ /= n_samples
#根據cholesky分解計算精度矩陣
self.precisions_cholesky_ = _compute_precision_cholesky(
self.covariances_, self.covariance_type)
然後重複以上過程,就完成了EM演算法的實現啦。
下面進入我們的實戰環節。。。
資料(可以去我的GitHub上拿,地址:https://github.com/LeBron-Jian/MachineLearningNote)
資料的背景是這樣的,這裡簡單介紹一下:在某個地區有一個橋,橋東面有一個區域,橋西邊有一個區域。假設我們這兩個地方是存放共享單車的,那給出的資料是每天某個時間點,共享單車被騎走的資料。(此資料是關於時間序列的資料),資料有 42312條,每條資料有兩個特徵(也就是前面提到的兩個地區)。
首先我們展示一下資料,程式碼如下:
import pandas as pd filename = 'Fremont.csv' data = pd.read_csv(filename, index_col='Date', parse_dates=True) res = data.head() print(res)
資料如下:
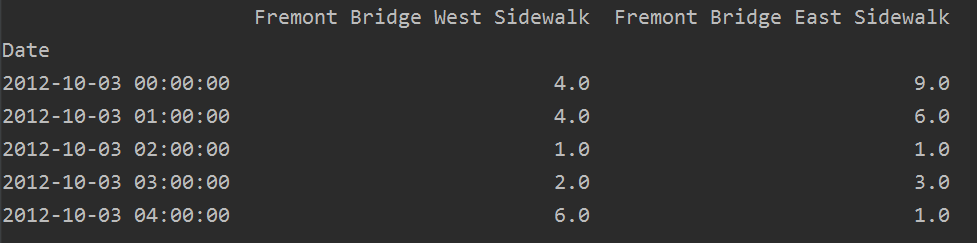
為了直觀,我們畫圖,看看原資料長什麼樣子:

這樣是很難看出特徵的吧,原資料是按照小時來統計兩個區域的資料,下面我們對資料進行重取樣,按周進行計算,我們再看看效果:
# 展示原資料
# data.plot()
data.resample('w').sum().plot()
注意這個resample 的意思,是按照時間索引進行合併後求和計算的。就是在給定的時間單位內重取樣,常見的時間頻率為:
- A year
- M month
- W week
- D day
- H hour
- T minute
- S second
說明白了意思,下面我們看看按周進行計算的圖:
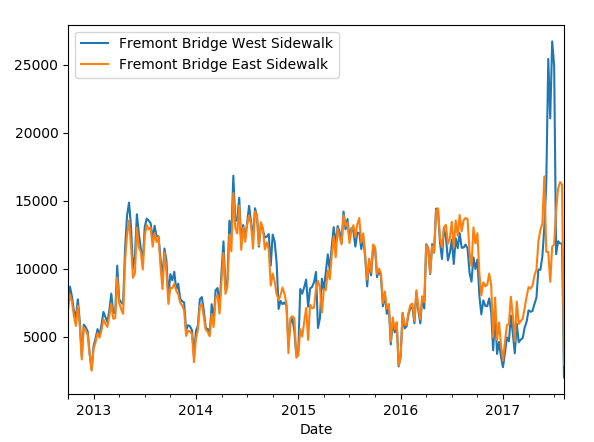
現在資料直觀上看起來清晰多了吧,當然我們對於時間序列問題,不止可以採取重取樣檢視資料,也可以採用滑動視窗,下面嘗試一下采用365天做一個滑動視窗,這裡是視窗的總和,程式碼和圖如下:
# 對資料採用滑動視窗,這裡視窗是365天一個
data.resample('D').sum().rolling(365).plot()
圖如下:
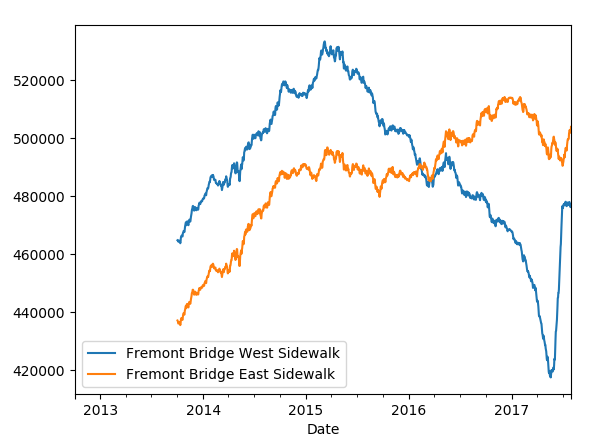
下面我們不按照時間來算了,不對這五年的資料進行分析了,我們想看看某一天的資料分佈,如何做呢?
# 檢視某一天的資料分佈 data.groupby(data.index.time).mean().plot() plt.xticks(rotation=45)
圖如下:

我們可以看到在早上七點到九點,West地區騎走的共享單車比較多,而在下午的四點到六點,East騎走的共享單車比較多。
下面我們將這兩個特徵分別命名為East和West,再看看前五個小時時間變換圖。
# 檢視前五個小時時間變換
# pivot table
data.columns = ['West', 'East']
data['Total'] = data['West'] + data['East']
pivoted = data.pivot_table('Total', index=data.index.time, columns=data.index.date)
res = pivoted.iloc[:5, :5]
print(res)
結果如下:

我們展示一下 24個小時的兩地資料圖:
# 畫圖展示一下 pivoted.plot(legend=False, alpha=0.01) plt.xticks(rotation=45)
圖如下(資料比較多,畫圖比較慢,等等就OK):
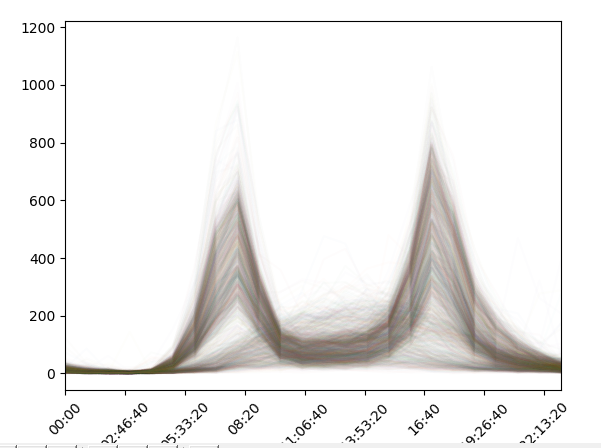
對資料分析完後,我們開始使用模型訓練,這裡為了能將資料展示在二維圖上,我們做這樣一個處理,首先我們將資料轉置,畢竟將資料分為很多特徵,而且只有24個數據不好。所以將樣本數分為1763,特徵為24個,則效果就比較好了。。。。
而這樣是可以做的,但是方便演示,我們希望將資料轉換為二維的,那我們需要對資料進行降維,我們把二十四個特徵降維到二維空間,降維程式碼如下:
X = pivoted.fillna(0).T.values print(X.shape) X2 = PCA(2).fit_transform(X) print(X2.shape) plt.scatter(X2[:, 0], X2[:, 1])
轉換為二維,資料如圖所示:
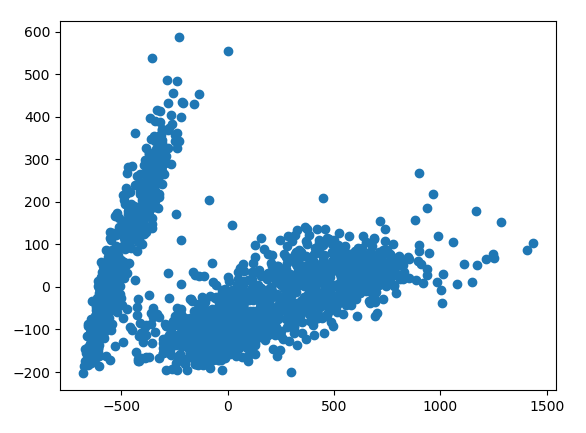
資料經過PCA降維後,其物理意義很難解釋,我們可以看到圖中都有負值了,所以不要糾結這個問題。
下面看GMM演算法的程式碼:
gmm = GaussianMixture(2) gmm.fit(X) labels_prob = gmm.predict_proba(X) print(labels_prob) labels = gmm.predict(X) print(labels) plt.scatter(X2[:, 0], X2[:, 1], c=labels, cmap='rainbow')
我們看看預測出來的label概率和label值(GMM演算法比較特別,我們可以知道某個類別的概率值):
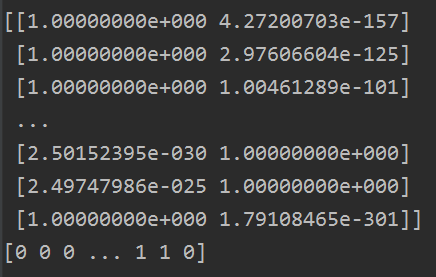
使用GMM演算法,分類的圖如下:
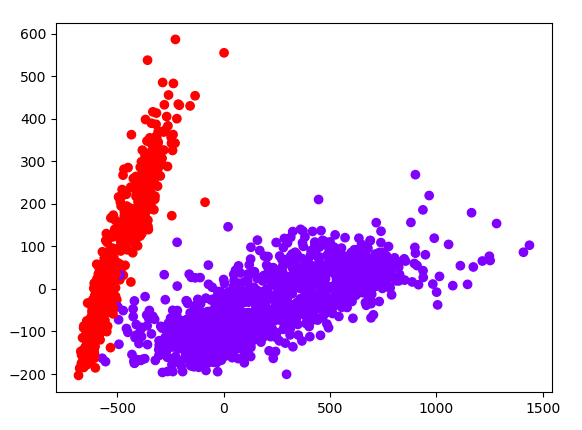
下面我們將二維資料還原回去,看效果,程式碼如下:
fig, ax = plt.subplots(1, 2, figsize=(14, 6))
pivoted.T[labels == 0].T.plot(legend=False, alpha=0.1, ax=ax[0])
pivoted.T[labels == 1].T.plot(legend=False, alpha=0.1, ax=ax[0])
ax[0].set_title('Purple Cluster')
ax[1].set_title('Red Cluster')
圖如下:
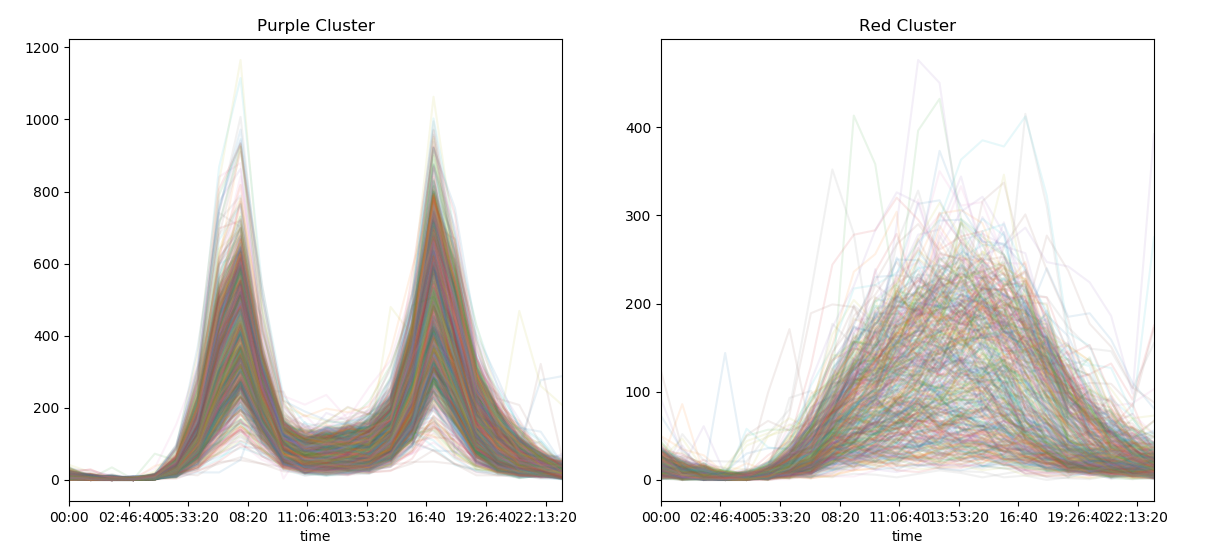
完整程式碼及其資料,請移步小編的GitHub
傳送門:請點選我
如果點選有誤:https://github.com/LeBron-Jian/MachineLearningNote
PS:這篇文章是我整理自己學習EM演算法的筆記,結合老師的PPT,然後找到網友優秀的部落格,將自己的理解寫到這裡。
參考文獻:https://www.cnblogs.com/pinard/p/6912636.html
https://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html
https://blog.csdn.net/fuqiuai/article/details/79484421
https://blog.csdn.net/u010834867/article/details/90762296
https://zhuanlan.zhihu.com/p/28108751
https://blog.csdn.net/lihou1987/article/details/70833229
https://blog.csdn.net/v_july_v/article/details/8170
