完整程式碼及其資料，請移步小編的GitHub

　　傳送門：請點選我

　　如果點選有誤：https://github.com/LeBron-Jian/MachineLearningNote

　　在資料探勘方面，經常需要在做特徵工程和模型訓練之前對資料進行清洗，剔除無效資料和異常資料。異常檢測也是資料探勘的一個方向，用於反作弊，偽基站，金融欺詐等領域。

　　在之前已經學習了異常檢測演算法One Class SVM和 isolation  Forest演算法，博文如下：

Python機器學習筆記：異常點檢測演算法——One Class SVM

Python機器學習筆記：異常點檢測演算法——Isolation Forest

　　下面學習一個新的異常檢測演算法：Local Outlier Factor

前言：異常檢測演算法

　　異常檢測方法，針對不同的資料形式，有不同的實現方法。常用的有基於分佈的方法，在上下 α 分位點之外的值認為是異常值（例如下圖），對於屬性值常用此類方法。基於距離的方法，適用於二維或高維座標體系內異常點的判別。例如二維平面座標或經緯度空間座標下異常點識別，可用此類方法。

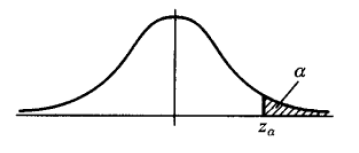
　　下面要學習一種基於距離的異常檢測演算法，區域性異常因子 LOF演算法（Local Outlier Factor）。此演算法可以在中等高維資料集上執行異常值檢測。

　　Local Outlier Factor（LOF）是基於密度的經典演算法（Breuning et,al 2000），文章發表與SIGMOD 2000 ，到目前已經有 3000+引用。在LOF之前的異常檢測演算法大多數是基於統計方法的，或者是借用了一些聚類演算法用於異常點的識別（比如：DBSCAN，OPTICS），但是基於統計的異常檢測演算法通常需要假設資料服從特定的概率分佈，這個假設往往是不成立的。而聚類的方法通常只能給出0/1的判斷（即：是不是異常點），不能量化每個資料點的異常程度。相比較而言，基於密度的LOF演算法要更簡單，直觀。它不需要對資料的分佈做太多要求，還能量化每個資料點的異常程度（outlierness）。

　　在學習LOF之前，可能需要了解一下KMeans演算法，這裡附上博文：

Python機器學習筆記：K-Means演算法，DBSCAN演算法

1，LOF（Local Outlier Factor）演算法理論

　　（此處地址：https://blog.csdn.net/wangyibo0201/article/details/51705966/）

1.1  LOF演算法介紹

　　LOF是基於密度的演算法，其最核心的部分是關於資料點密度的刻畫。如果對 distanced-based 或者 density-based 的聚類演算法有些印象，你會發現 LOF中用來定義密度的一些概念和K-Means演算法一些概念很相似。

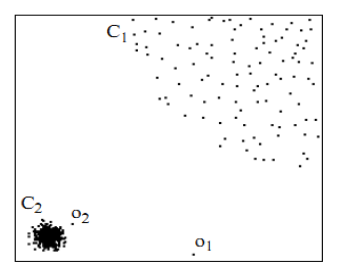
　　首先用視覺直觀的感受一下，如下圖，對於C1集合的點，整體間距，密度，分散情況較為均勻一致。可以認為是同一簇；對於C2集合點，同樣可認為是一簇。o1,  o2點相對孤立，可以認為是異常點或離散點。現在的問題是，如何實現演算法的通用性，可以滿足C1 和 C2 這種密度分散情況迥異的集合的異常點識別。LOF可以實現我們的目標，LOF不會因為資料密度分散情況不同而錯誤的將正確點判定為異常點。

1.2  LOF 演算法步驟

 　　下面介紹 LOF演算法的相關定義：

（1） d(p, o) ：兩點 P 和 O 之間的距離

（2） K-distance：第 k 距離

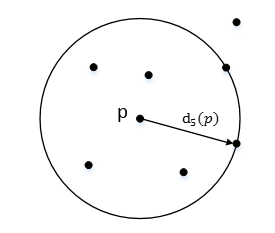
　　在距離資料點 p 最近的 幾個點中，第 k 個最近的點跟點 p 之間的距離稱為點 p的K-鄰近距離，記為 K-distance(p)。

　　對於點 p 的第 k 距離 dk(p) 定義如下：

　　　　dk(p) = d(p, o) 並且滿足：

　　　　（a）在集合中至少有不包括 p 在內的 k 個點 o ∈ C{x≠p}，滿足d(p,o') ≤ d(p,o)

　　　　（b）在集合中最多不包括 p 在內的 k-1 個點 o ∈ C{x≠p}，滿足d(p,o') ≤ d(p,o)

　　p 的第 k 距離，也就是距離 p 第 k 遠的點的距離，不包括 P，如下圖所示：

（3） k-distance neighborhood of p：第 k 距離鄰域

　　點 p 的第 k 距離鄰域 Nk(p) 就是 p 的第 k距離即以內的所有點，包括第 k 距離。

　　因此 p 的 第 k 鄰域點的個數 |Nk(p)| >=k

（4） reach-distance：可達距離

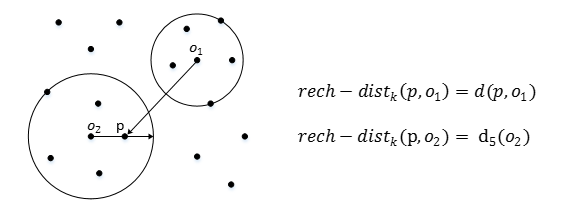
　　可達距離（Reachablity distance）：可達距離的定義跟K-鄰近距離是相關的，給定引數k時，資料點 p 到 資料點o的可達距離 reach-dist(p, o)為資料點 o 的 K-鄰近距離和資料點 p與點o 之間的直接距離的最大值。

　　點 o 到 點 p 的第 k 可達距離定義為：

　　也就是，點 o 到點 p 的第 k 可達距離，至少是 o 的第 k 距離，或者為 o, p之間的真實距離。這也意味著，離點 o 最近的 k 個點， o 到他們的可達距離被認為是相等，且都等於 dk(o)。如下圖所示， o1 到 p 的第 5 可達距離為 d(p, o1)，o2 到 p 的第5可達距離為 d5(o2)

（5） local reachablity density：區域性可達密度

　　區域性可達密度（local reachablity density）：區域性可達密度的定義是基於可達距離的，對於資料點 p，那些跟 點 p的距離小於等於 K-distance(p) 的資料點稱為它的 K-nearest-neighbor，記為Nk(p)，資料點p的區域性可達密度為它與鄰近的資料點的平均可達距離的導數。

　　點 p 的區域性可達密度表示為：

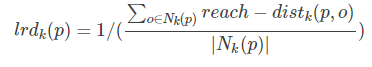
　　表示點 p 的第 k 鄰域內點到 p 的平均可達距離的倒數。

　　注意：是 p 的鄰域點 Nk(p)到 p的可達距離，不是 p 到 Nk(p) 的可達距離，一定要弄清楚關係。並且，如果有重複點，那麼分母的可達距離之和有可能為0，則會導致 ird 變為無限大，下面還會繼續提到這一點。

　　這個值的含義可以這樣理解，首先這代表一個密度，密度越高，我們認為越可能屬於同一簇，密度越低，越可能是離群點，如果 p 和 周圍鄰域點是同一簇，那麼可達距離越可能為較小的 dk(o)，導致可達距離之和較小，密度值較高；如果 p 和周圍鄰居點較遠，那麼可達距離可能都會取較大值 d(p, o)，導致密度較小，越可能是離群點。

（6） local outlier factor：區域性離群因子

　　Local Outlier Factor：根據區域性可達密度的定義，如果一個數據點根其他點比較疏遠的話，那麼顯然它的區域性可達密度就小。但LOF演算法衡量一個數據點的異常程度，並不是看他的絕對區域性密度，而是它看跟周圍鄰近的資料點的相對密度。這樣做的好處是可以允許資料分佈不均勻，密度不同的情況。區域性異常因子既是用區域性相對密度來定義的。資料點 p 的區域性相對密度（區域性異常因子）為點 p 的鄰居們的平均區域性可達密度跟資料點 p 的區域性可達密度的比值。

　　點 p 的區域性離群因子表示為：

　　表示點 p 的鄰域點 Nk(p) 的區域性可達密度與點 p的區域性可達密度之比的平均數。

　　LOF 主要通過計算一個數值 score 來反映一個樣本的異常程度。這個數值的大致意思是：一個樣本點周圍的樣本點所處位置的平均密度比上該樣本點所在位置的密度。如果這個比值越接近1，說明 p 的其鄰域點密度差不多， p 可能和鄰域同屬一簇；如果這個比值越小於1，說明 p 的密度高於其鄰域點目睹，p 為密度點；如果這個比值越大於1，說明 p 的密度小於其鄰域點密度， p 越可能是異常點。

　　所以瞭解了上面LOF一大堆定義，我們在這裡簡單整理一下此演算法：

• 1，對於每個資料點，計算它與其他所有點的距離，並按從近到遠排序
• 2，對於每個資料點，找到它的K-Nearest-Neighbor，計算LOF得分

1.3  演算法應用

　　LOF 演算法中關於區域性可達密度的定義其實暗含了一個假設，即：不存在大於等於k個重複的點。當這樣的重複點存在的時候，這些點的平均可達距離為零，區域性可達密度就變為無窮大，會給計算帶來一些麻煩。在實際應用中，為了避免這樣的情況出現，可以把 K-distance改為 K-distinct-distance，不考慮重複的情況。或者，還可以考慮給可達距離都加一個很小的值，避免可達距離等於零。

　　LOF演算法需要計算資料點兩兩之間的距離，造成整個演算法時間複雜度為 O(n**2)。為了提高演算法效率，後續有演算法嘗試改進。FastLOF（Goldstein, 2012）先將整個資料隨機的分成多個子集，然後在每個子集裡計算 LOF值。對於那些LOF異常得分小於等於1的。從資料集裡剔除，剩下的在下一輪尋找更合適的 nearest-neighbor，並更新LOF值。這種先將資料粗略分為多個部分，然後根據區域性計算結果將資料過濾減少計算量的想法，並不罕見。比如，為了改進 K-Means的計算效率，Canopy Clustering演算法也採用過比較相似的做法。

2，LOF演算法應用（sklearn實現）

2.1  sklearn 中LOF庫介紹

　　Unsupervised Outlier Detection using Local Outlier Factor （LOF）。

　　The anomaly score of each sample is called Local Outlier Factor. It measures the local deviation of density of a given sample with respect to its neighbors. It is local in that the anomaly score depends on how isolated the object is with respect to the surrounding neighborhood. More  precisely, locality is given by k-nearest neighbors, whose distance is used to estimate the local density. By comparing the local density of a sample to the local densityes of its neighbors, one can identify samples that have s substantially lower density than their neighbors. These are considered outliers.

　　區域性離群點因子為每個樣本的異常分數，主要是通過比較每個點 p 和其鄰域點的密度來判斷該點是否為異常點，如果點p的密度越低，越可能被認定是異常點。至於密度，是通過點之間的距離計算的，點之間的距離越遠，密度越低，距離越近，密度越高。而且，因為LOF對密度的是通過點的第 k 鄰域來計算，而不是全域性計算，因此得名 “區域性”異常因子。

　　Sklearn中LOF在 neighbors 裡面，其原始碼如下：

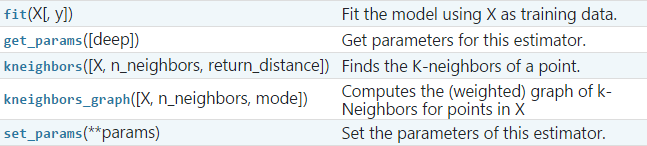
 　　LOF的中主要引數含義：

• n_neighbors：設定k，default=20
• contamination：設定樣本中異常點的比例，default=auto

　　LOF的主要屬性：

 　　補充一下這裡的 negative_outlier_factor_：和LOF相反的值，值越小，越有可能是異常值。（LOF的值越接近1，越有可能是正常樣本，LOF的值越大於1，則越有可能是異常樣本）

 　　LOF的主要方法：

2.2  LOF演算法實戰

例項1：在一組數中找異常點

　　程式碼如下：

import numpy as np
from sklearn.neighbors import LocalOutlierFactor as LOF

X = [[-1.1], [0.2], [100.1], [0.3]]
clf = LOF(n_neighbors=2)
res = clf.fit_predict(X)
print(res)
print(clf.negative_outlier_factor_)

'''
如果 X = [[-1.1], [0.2], [100.1], [0.3]]
[ 1  1 -1  1]
[ -0.98214286  -1.03703704 -72.64219576  -0.98214286]

如果 X = [[-1.1], [0.2], [0.1], [0.3]]
[-1  1  1  1]
[-7.29166666 -1.33333333 -0.875      -0.875     ]

如果 X = [[0.15], [0.2], [0.1], [0.3]]
[ 1  1  1 -1]
[-1.33333333 -0.875      -0.875      -1.45833333]
'''

 　　我們可以發現，隨著數字的改變，它的異常點也在變，無論怎麼變，都是基於鄰域密度比來衡量。

 例項2：Outlier detection

　　（outlier detection：當訓練資料中包含離群點，模型訓練時要匹配訓練資料的中心樣本，忽視訓練樣本的其他異常點）

　　The Local Outlier Factor（LOF） algorithm is an unsupervised anomaly detection method which computes the local density deviation of a given data point with respect to its neighbors. It considers as outliers the samples that have a substantially lower density than their neighbors.

　　This example shows how to use LOF for outlier detection which is the default use case of this estimator in sklearn。Note that when LOF is used for outlier detection it has no predict, decision_function and  score_samples methods.

　　The number of neighbors considered（parameter n_neighbors）is typically set 1) greater than the minimum number of samples a cluster has to contain, so that other samples can be local outliers relative to this cluster , and 2) smaller than the maximum number of close by samples that can potentially be local outliers. In practice, such informations are generally not available and taking n_neighbors=20 appears to work well in general.

 　　鄰居的數量考慮（引數 n_neighbors通常設定為：

• 1） 大於一個叢集包含最小數量的樣本，以便其他樣本可以區域性離群
• 2） 小於附加的最大數量樣本，可以區域性離群值

 　　在實踐中，這種資訊一般是不可用的，n_neighbors=20 似乎實踐很好。

　　程式碼：

#_*_coding:utf-8_*_
import numpy as np
from sklearn.neighbors import LocalOutlierFactor as LOF
import matplotlib.pyplot as plt

# generate train data
X_inliers = 0.3 * np.random.randn(100, 2)
X_inliers = np.r_[X_inliers + 2, X_inliers - 2]


# generate some outliers
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))
X = np.r_[X_inliers, X_outliers]

n_outliers = len(X_outliers)  # 20
ground_truth = np.ones(len(X), dtype=int)
ground_truth[-n_outliers:] = -1

# fit the model for outlier detection
clf = LOF(n_neighbors=20, contamination=0.1)

# use fit_predict to compute the predicted labels of the training samples
y_pred = clf.fit_predict(X)
n_errors = (y_pred != ground_truth).sum()
X_scores = clf.negative_outlier_factor_


plt.title('Locla Outlier Factor (LOF)')
plt.scatter(X[:, 0], X[:, 1], color='k', s=3., label='Data points')
# plot circles with radius proportional to thr outlier scores
radius = (X_scores.max() - X_scores) / (X_scores.max() - X_scores.min())
plt.scatter(X[:, 0], X[:, 1], s=1000*radius, edgecolors='r',
    facecolors='none', label='Outlier scores')
plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.xlabel("prediction errors: %d"%(n_errors))
legend = plt.legend(loc='upper left')
legend.legendHandles[0]._sizes = [10]
legend.legendHandles[1]._sizes = [20]
plt.show()

 　　結果如下：

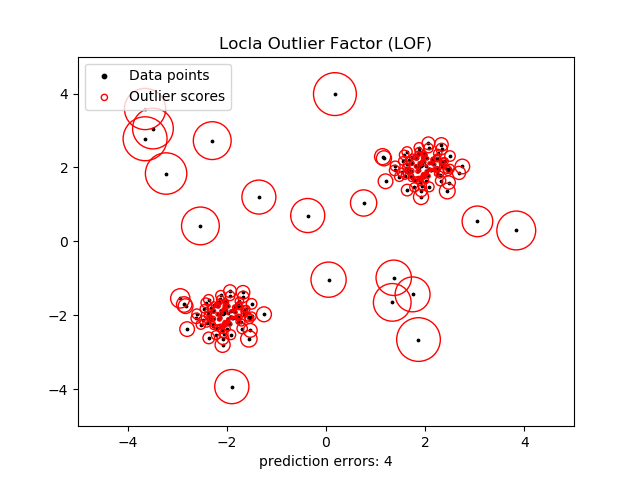
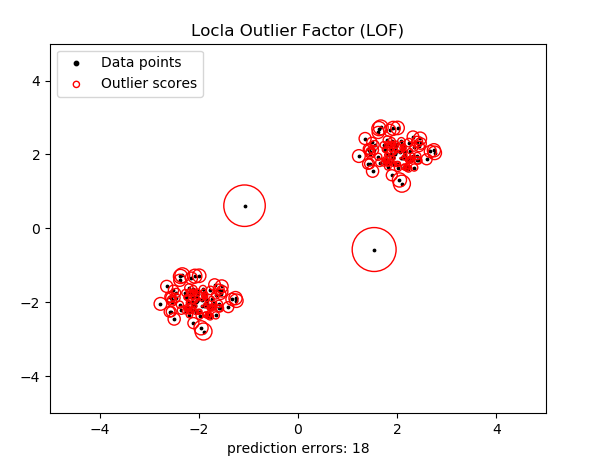
 　　這個圖可能有點複雜。這樣我們將異常點設定為2個，則執行效果：

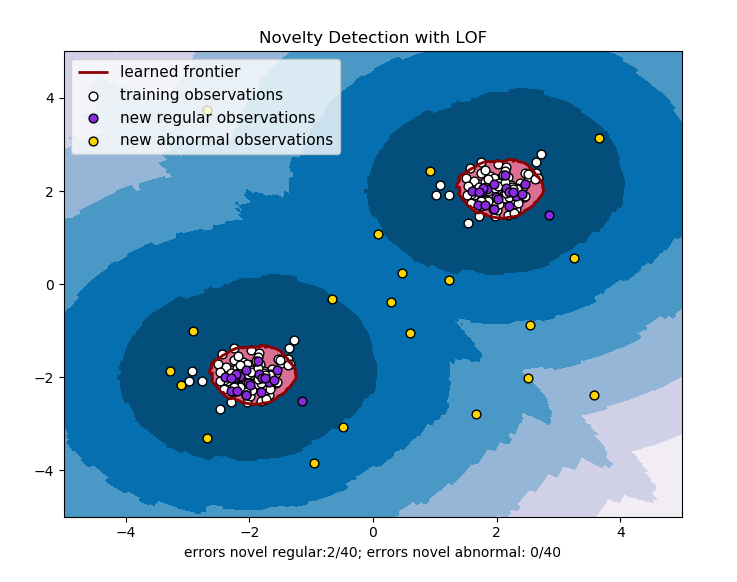
例項3：Novelty detection

　　（novelty detection：當訓練資料中沒有離群點，我們的目的是用訓練好的模型去檢測另外發現的新樣本。）

　　The Local Outlier Factor（LOF） algorithm is an unsupervised anomaly detection method which computes the local density deviation of a given data point with respect to its neighbors. It considers as outliers the samples that have a substantially lower density than their neighbors.

　　This example shows how to use LOF for novelty detection .Note that when LOF is used for novelty detection  you MUST not use no predict, decision_function and  score_samples on the training set as this would lead to wrong result. you must only use these methods on new unseen data（which are not in the training set）

　　The number of neighbors considered（parameter n_neighbors）is typically set 1) greater than the minimum number of samples a cluster has to contain, so that other samples can be local outliers relative to this cluster , and 2) smaller than the maximum number of close by samples that can potentially be local outliers. In practice, such informations are generally not available and taking n_neighbors=20 appears to work well in general.

 　　程式碼如下：

#_*_coding:utf-8_*_
import numpy as np
from sklearn.neighbors import LocalOutlierFactor as LOF
import matplotlib.pyplot as plt
import matplotlib


# np.meshgrid() 生成網格座標點
xx, yy = np.meshgrid(np.linspace(-5, 5, 500), np.linspace(-5, 5, 500))

# generate normal  (not abnormal) training observations  
X = 0.3*np.random.randn(100, 2)
X_train = np.r_[X+2, X-2]

# generate new normal (not abnormal) observations
X = 0.3*np.random.randn(20, 2)
X_test = np.r_[X+2, X-2]

# generate some abnormal novel observations
X_outliers = np.random.uniform(low=-4, high=4, size=(20, 2))


# fit the model for novelty detection  (novelty=True)
clf = LOF(n_neighbors=20, contamination=0.1, novelty=True)
clf.fit(X_train)

# do not use predict, decision_function and score_samples on X_train
# as this would give wrong results but only on new unseen data(not 
# used in X_train , eg: X_test, X_outliers or the meshgrid)
y_pred_test = clf.predict(X_test)
y_pred_outliers = clf.predict(X_outliers)
'''
### contamination=0.1
X_test: [ 1  1  1  1  1  1  1  1  1  1  1  1  1  1 -1  1  1 -1  1  1  1  1  1  1
  1  1  1  1  1  1  1  1  1  1 -1  1  1 -1  1  1]

### contamination=0.01
X_test: [1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1]

y_pred_outliers: [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
'''

n_error_test = y_pred_test[y_pred_test == -1].size
n_error_outliers = y_pred_outliers[y_pred_outliers == 1].size

# plot the learned frontier, the points, and the nearest vectors to the plane
Z = clf.decision_function(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

plt.title('Novelty Detection with LOF')
plt.contourf(xx, yy, Z, levels=np.linspace(Z.min(), 0, 7), cmap=plt.cm.PuBu)
a = plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='darkred')
plt.contourf(xx, yy, Z, levels=[0, Z.max()], colors='palevioletred')

s = 40
b1 = plt.scatter(X_train[:, 0], X_train[:, 1], c='white', s=s, edgecolors='k')
b2 = plt.scatter(X_test[:, 0], X_test[:, 1], c='blueviolet', s=s, edgecolors='k')

c = plt.scatter(X_outliers[:, 0], X_outliers[:, 1], c='gold', s=s, edgecolors='k')

plt.axis('tight')
plt.xlim((-5, 5))
plt.ylim((-5, 5))
plt.legend([a.collections[0], b1, b2, c],
            ["learned frontier", "training observations",
            "new regular observations", "new abnormal observations"],
            loc='upper left',
            prop=matplotlib.font_manager.FontProperties(size=11))

plt.xlabel("errors novel regular:%d/40; errors novel abnormal: %d/40"
    %(n_error_test, n_error_outliers))
plt.show()

 　　效果如下：

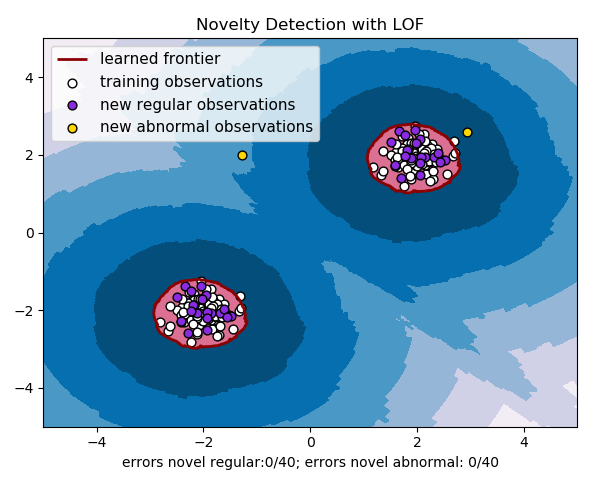
 　　對上面模型進行調參，並設定異常點個數為2個，則效果如下：

 參考地址：

https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.LocalOutlierFactor.html?highlight=lof

 https://blog.csdn.net/YE1215172385/article/details/79766906

https://blog.csdn.net/bbbeoy/article/details/8030